
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Электрические моменты ядер
|
|
Электрические моменты ядер, определяются по поведению их в электрическом поле.
Выделяют электрические моменты разных порядков:
- электрический момент нулевого порядка – это электрический заряд ядра (скаляр);
- электрический момент первого порядка – это дипольный момент ядра (вектор);
-
- электрический момент второго порядка – это квадрупольный момент ядра (тензор).
-
Энергия ядра, помещенного в электрическое поле, связанная с моментом нулевого порядка равна:
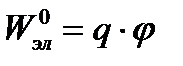
Дипольный момент ядра будет определяться по формуле:
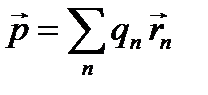
где 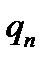 заряд n – ного протона, а
заряд n – ного протона, а  – расстояние n – ного протона от центра симметрии ядра.
– расстояние n – ного протона от центра симметрии ядра.
Энергия ядра, помещенного в электрическое поле, связанная с моментом первого порядка равна:
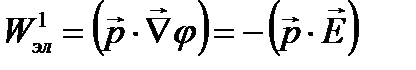
Квадрупольный момент ядра 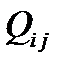 определяется по формуле:
определяется по формуле:
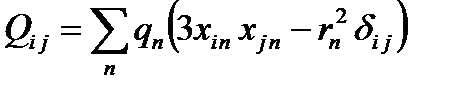
Энергия ядра, помещенного в электрическое поле, связанная с квадрупольным моментом равна:
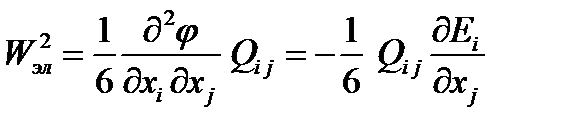
Электрический заряд ядра Ze не дает представления о распределении протонов в ядре.
Некоторые представления о распределении электрического заряда в ядре и его структуре можно получить с помощью дипольного и квадрупольного моментов ядра.
Диполем называется система из двух равных по величине зарядов q разного знака, жестко закрепленных на расстоянии d. Такая система, имея равный нулю электрический заряд, обладает свойством ориентироваться по направлению электрического поля.
Так как отрицательных зарядов в ядре нет, то смещение положительного заряда (протонов) относительно нулевого (нейтронов) вызывает появление дипольного момента и ядро поворачивается в электрическом поле относительно центра инерции.
Обычно рассматривают проекцию дипольного момента ядра на ось OZ, совпадающую с направлением внешнего электрического поля.
Экспериментальные измерения показывают, что ядра в основном состоянии имеют всегда равный нулю электрический дипольный момент.
Сильное электрическое поле может вызывать поляризацию протонов в ядре и возникновение дипольного момента.
Например, электромагнитное поле γ-кванта может вызывать периодическое смещение протонов относительно нейтронов и возникновение дипольных колебаний протонов в ядре.
Другая характеристика ядра – квадрупольный электрический момент 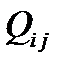 , который не равен нулю для многих ядер, находящихся даже в стационарных состояниях.
, который не равен нулю для многих ядер, находящихся даже в стационарных состояниях.
Квадрупольный момент определяет степень взаимодействие ядра с неоднородным электрическим полем.
Для сферически симметричного распределения электрического заряда 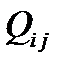 = 0.
= 0.
Квадрупольный момент является мерой отклонения распределения электрического заряда от сферически симметричного.
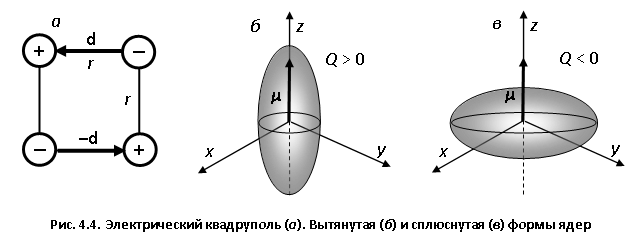
!!!Величина 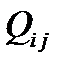 положительна для вытянутых ядер, и отрицательна – для сплюснутых.
положительна для вытянутых ядер, и отрицательна – для сплюснутых.
Дважды магические ядра – ядра сферические; в целом же сферических ядер мало.
В интервале между соседними магическими числами ядра меняют форму в такой последовательности: сферическое, сплюснутое, сферическое, вытянутое, сильно вытянутое, вытянутое, сферическое
Квадрупольные момент имеет размерность площади и часто измеряется в единицах барн,
1 барн = 10 –24 см2.
Ниже приведены величины Q для нескольких ядер. Существуют ядра как вытянутые, так и сплюснутые. Все магические ядра имеют сферическую форму (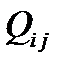 = 0), которая, таким образом, соответствует наиболее устойчивым ядрам.
= 0), которая, таким образом, соответствует наиболее устойчивым ядрам.
| Ядро | J | Q, барн | Ядро | J | Q, барн |
| 2H | 0,0028 | 137 Cs | 7/2 | 0,045 | |
| 4He | 235 U | 7/2 | 4,1 |
Для экспериментального определения квадрупольных моментов используются те же методы, что и для измерения магнитных моментов - изучение сверхтонкой структуры оптических линий в спектрах и радиочастотные методы.
Выполнение закона сохранения четности приводит к правилам отбора для электромагнитного излучения атомов и ядер, для радиоактивных превращений и ядерных реакций.
Основные состояния четно-четных ядер всегда имеют положительную четность. У других ядер основные состояния могут быть как четными, так и нечетными. Ядра в возбужденных состояниях могут иметь различную четность, не обязательно совпадающую с четностью основного состояния.
Четность отмечается знаком плюс или минус рядом с обозначением спина ядра  (например, 0+, 3− и т.п.).
(например, 0+, 3− и т.п.).
Ядро с заполненными уровнями (подоболочками).
Так как на каждой из подоболочек заняты все состояния со всеми возможными проекциями вектора углового момента J, каждому нуклону с проекцией + jz соответствует нуклон с проекцией – jz.
результирующий угловой момент ядра, т.е. спин ядра, равен нулю.
Четность замкнутой подоболочки положительна, так как она образована парами нуклонов с одинаковой четностью. для замкнутой подоболочки
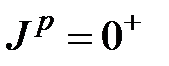 .
.
2) Ядро с одним нуклоном сверх заполненных подоболочек.
Остов заполненных подоболочек имеет характеристики 0+, и спин и четность определяются квантовыми числами единственного внешнего нуклона.
Если этот нуклон находится в состоянии nlj, то спин ядра равен j, а четность P = (–1) l.
Поэтому для основного состояния такого ядра
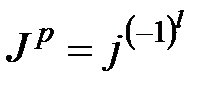 .
.
3) Ядро с вакансией в заполненной подоболочке. Такому ядру для заполнения подоболочки не хватает одного нуклона.
Пусть состояние нуклона на такой подоболочке будет nlj.
Обозначим момент и четность подоболочки с вакансией как j’ и P’.
Так как добавление нуклона на подоболочку с вакансией замыкает ее, то J + J ’ = 0 и P ∙ P ’ = +1, откуда j ’ = j и P ’ = P, т.е. имеем те же правила (4.2) нахождения спина и четности основного состояния, что и для ядра с одним нуклоном сверх замкнутых подоболочек
Капельная модель ядра. (см лекцию 3а)
Date: 2015-07-24; view: 1053; Нарушение авторских прав