Спин ядра

Ядро, как пространственно ограниченная и связанная система взаимодействующих между собой нуклонов, во может рассматриваться в целом как одна микрочастица.

Так как нуклоны, из которых состоит ядро, обладают собственным механическим моментом, или спином, а также совершают движение относительно друг друга (орбитальное движение относительно центра инерции ядра), то и ядра должны иметь собственный механический момент (далее просто момент) или спин.

Спин ядра 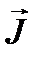есть векторная сумма полных моментов отдельных нуклонов, каждый из которых складывается из орбитального момента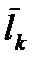

и спина нуклона 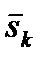, так что

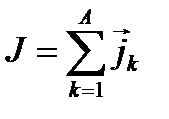
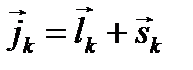
Вектор спина ядра, обладает своеобразными свойствами.

1. Абсолютная величина вектора момента любой изолированной физической величины может принимать только дискретные значения:

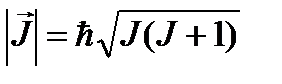
где J – либо целое, либо полуцелое положительное число:

J = 0, 1/2, 1, 3/2,...

Число J называют обычно величиной момента или квантовым числом момента.

квантовое число 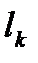для орбитального момента всегда целое число, 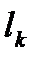= 0, 1, 2, …, а нуклоны имеют квантовое число спина 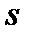= 1/2 (спин равен ½ ħ).

2. Проекция момента 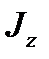может принимать случайным образом одно из (2 J + 1) значений, изменяющихся от 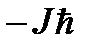до 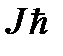через единицу.

.

В отношении спинов различных ядер наблюдаются следующие опытные закономерности:

а) Для ядер с четными А спины всегда целые, а при нечетном А – всегда полуцелые.

б) Четно-четные ядра (А - четное) в основном состоянии имеют спин равный нулю.

Этот факт дает основания считать, что одноименные нуклоны объединяются в пары (эффект спаривания,) с противоположно направленными спинами, так что суммарный момент импульса оказывается равным нулю.

в) Нечетно-нечетные ядра (А - четное) имеют целочисленный спин.

Это указывает на то, что разноименные нуклоны объединяются в пары с одинаковым направлением спинов, создавая единичный момент.

Магнитный момент ядра

Магнитный момент – основная физическая величина, характеризующая магнитные свойства вещества.

Магнитными моментами обладают элементарные частицы, атомные ядра, электронные оболочки атомов и молекул.

Магнитные моменты отдельных элементарных частиц (электронов, протонов, нейтронов) обусловлены существованием у них спина.

Магнитные моменты ядер складываются из спиновых магнитных моментов протонов и нейтронов, образующих эти ядра, а также из магнитных моментов, связанных с их орбитальным движением внутри ядра по тем же правилам, по которым вычисляется спин ядра.

Магнитный момент ядра равен

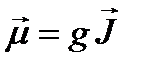
где g – гиромагнитный множитель (отношение), равный отношению величины магнитного момента к величине механического:

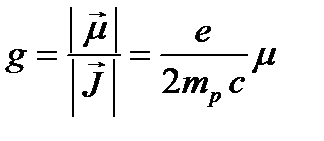
е – элементарный электрический заряд;

m_p – масса протона;

с – скорость света в вакууме;

μ – безразмерное число.

Проекция магнитного момента 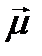на ось OZ, которая совпадает с направлением внешнего магнитного поля, будет равна:

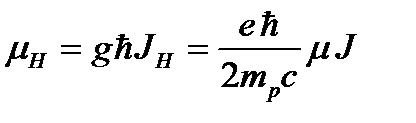
где величина

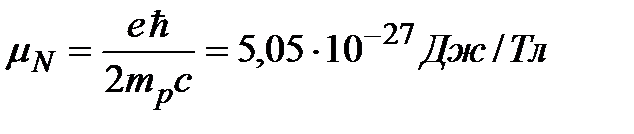
называется ядерным магнетоном.

Ядерный магнетон является такой же универсальной единицей измерения магнитных моментов ядер, какой служит элементарный электрический заряд е для измерения заряда тел, или постоянная Планка 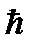для измерения механических моментов.

Безразмерное число μ служит для измерения магнитных моментов ядер в единицах ядерных магнетонов.

Методы экспериментального определения спина и магнитного момента ядер тесно между собой связаны и основаны на исследовании взаимодействия магнитного момента ядра с магнитным полем.

Исторически одним из первых методов определения спина ядер было исследование сверхтонкой структуры спектральных линий атомов, возникающей в результате взаимодействия магнитного момента ядра 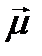с магнитным полем 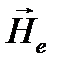, которое создается электронной оболочкой атома в месте расположения ядра.

Особенно точным методом определения магнитных моментов ядер является метод ядерного магнитного резонанса (ЯМР).

Идея метода заключается в принудительном изменении ориентации магнитного момента ядра (а, следовательно, и спина), находящегося в сильном магнитном поле, под действием слабого высокочастотного магнитного поля определенной (резонансной) частоты ω₀.

Если образец поместить в сильное постоянное внешнее магнитное поле 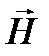, то магнитный момент 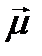будет прецессировать вокруг направления с частотой ω₀.

Энергия взаимодействия магнитного момента ядра и сильного магнитного поля равна

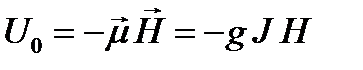
и соответствует низшему энергетическому состоянию атома.

Для перехода на первый возбужденный уровень нужна энергия

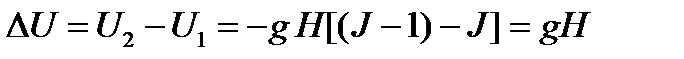
которой соответствует квант энергии 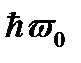, т.е.

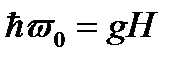
По найденному таким образом значению ω₀ находят гиромагнитное отношение, а из него - магнитный момент в безразмерных величинах μ.

Резонансные методы измерения магнитных моментов отличаются высокой точностью (до 6 знаков). Метод магнитного резонанса имеет несколько модификаций, в зависимости от способа обнаружения переориентации магнитных моментов в резонансном поле.

Этот метод был успешно использован для измерения магнитного момента нейтрона с той только разницей, что вместо образцов, содержащих ядра, использовались нейтронные пучки.

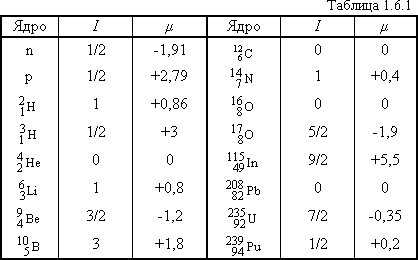
В таблице 1.6.1 приведены спины I и приближенные значения магнитных моментов для нуклонов и некоторых легких, средних и тяжелых ядер. Знак минус у магнитного момента указывает на то, что он направлен противоположно спину.

Ядра, имеющие нулевой спин, обладают нулевым магнитным моментом.

Отличие магнитных моментов нуклонов от целочисленных значений (в единицах, равных ядерному магнетону), а также наличие магнитного момента у нейтрона, имеющего нулевой электрический заряд, еще не объяснено полностью. Однако эти факты с определенностью указывают на некоторую сложную структуру нуклонов.

Date: 2015-07-24; view: 1253; Нарушение авторских прав