
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Применив закон сохранения импульса, можем написать
|
|
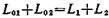 , или
, или 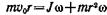 ,
,
откуда
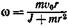 (4)
(4)
где 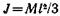 — момент инерции системы стержень — пуля.
— момент инерции системы стержень — пуля.
Если учесть, что в (4) 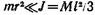 , а также что
, а также что 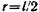 , то
, то
после несложных преобразований получим
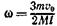 (5)
(5)
Подставив числовые значения величин в (5), найдем
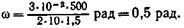
|
| По (3) получим |
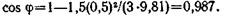
|
Следовательно, 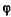 =9°20'.
=9°20'.
Задачи
Момент инерции
3.1. Определить момент инерции J материальной точки массой m =0,3 кг относительно оси, отстоящей от точки на r =20 см.
3.2. Два маленьких шарика массой m =10 г каждый скреплены тонким невесомым стержнем длиной l =20 см. Определить момент инерции J системы относительно оси, перпендикулярной стержню и проходящей через центр масс.
| Рис. 3.8 |
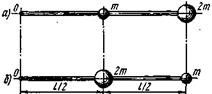
3.3. Два шара массами m и 2 m (m =10 г) закреплены на тонком невесомом стержне длиной l =40 см так, как это указано на рис. 3.7, а, б. Определить моменты инерции J системы относительно оси, перпендикулярной стержню и проходящей через его конец в этих двух случаях. Размерами шаров пренебречь.
|
|
| Рис. 3.7 |
|
лярной стержню и проходящей через: 1) его конец; 2) его середину; 3) точку, отстоящую от конца стержня на 1/3 его длины.
3.7. Определить момент инерции J тонкого однородного стержня длиной l =60 см и массой m =100 г относительно оси, перпендикулярной ему и проходящей через точку стержня, удаленную на а =20 см от одного из его концов.
3.8. Вычислить момент инерции J проволочного прямоугольника со сторонами а =12 см и b =16 см относительно оси, лежащей в плоскости прямоугольника и проходящей через середины малых сторон. Масса равномерно распределена по длине проволоки с линей ной плотностью τ=0,1 кг/м.
|
3.9. Два однородных тонких стержня: АВ длиной l 1=40 см • и массой m 1=900 г и CD длиной l 2=40 см и массой l 2=400 г скреплены под прямым углом (рис. 3.9). Определить момент инерции J системы стержней относительно оси 00', проходящей через конец стержня АВ параллельно стержню CD.
| Рис. 3.9 |
| Рис. 3.10 |
3.10. Решить предыдущую задачу для случая, когда ось 00' проходит через точку А перпендикулярно плоскости чертежа.
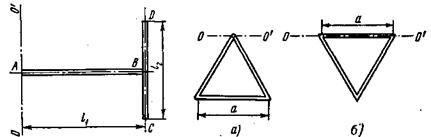
3.11. Определить момент инерции J проволочного равностороннего треугольника со стороной а =10 см относительно: 1) оси, лежащей в плоскости треугольника и проходящей через его вершину параллельно стороне, противоположной этой вершине (рис. 3.10, а); 2) оси, совпадающей с одной из сторон треугольника (рис. 3.10, б). Масса т треугольника равна 12 г и равномерно распределена по длине проволоки.
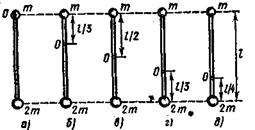
3.12. На концах тонкого однородного стержня длиной l и массой 3 m прикреплены маленькие шарики массами m и 2 m. Определить момент инерции J такой системы относительно оси, перпендикулярной стер и проходящей через точку О, лежащую на оси стержня. Вычисления выполнить для случаев а, б, в, г, д, изображенных на рис. 3.11. При расчетах принять l =1 м, m =0,1 кг. Шарики рассматривать как материальные точки.
3.13. Найти момент инерции J тонкого однородного кольца радиусом R =20 см и массой m =100 г относительно оси, лежащей в плоскости кольца и проходящей через его центр.
3.14. Определить момент инерции J кольца массой т =50 г и радиусом R =10 см относительно оси, касательной к кольцу.
|
|
| Рис. 3.11 |
| Рис. 3.12 |
3.15. Диаметр диска d =20 см, масса т =800 г. Определить момент инерции J диска относительно оси, проходящей через середину одного из радиусов перпендикулярно плоскости диска.
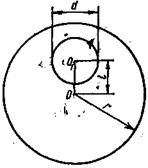
3.16. В однородном диске массой т =1 кг и радиусом r=30 см вырезано круглое отверстие диаметром d=20 см, центр которого находится на расстоянии l =15 см от оси диска (рис. 3.12). Найти момент инерции J полученного тела относительно оси, проходящей перпендикулярно плоскости диска через его центр.
3.17. Найти момент инерции J плоской однородной прямоугольной пластины массой т =800 г относительно оси, совпадающей с одной из ее сторон, если длина а другой стороны равна 40 см.
3.18. Определить момент инерции J тонкой плоской пластины со сторонами а =10 см и b =20 см относительно оси, проходящей
|
через центр масс пластины параллельно большей стороне. Масса пластины равномерно распределена по ее площади с поверхностной плотностью σ=1,2 кг/м2.
Основное уравнение динамики вращательного движения
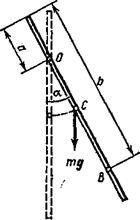
3.19. Тонкий однородный стержень длиной l =1 м может свободно вращаться вокруг горизонтальной оси, проходящей через точку О на стержне (рис. 3.13). Стержень отклонили от вертикали на угол а и отпустили. Определить для начального момента времени угловое в и тангенциальное аt ускорения точки В на стержне. Вычисления произвести для следующих случаев:
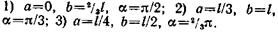
| Рис. 3.13 |
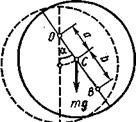
3.20. Однородный диск радиусом R = 10 см может свободно вращаться вокруг горизонтальной оси, перпендикулярной плоскости
диска и проходящей через точку О на нем (рис. 3.14). Диск отклонили на угол а и отпустили. Определить для начального момента времени угловое ε и тангенциальное а т ускорения точки В, находящейся на диске. Вычисления выполнить для следующих случаев:
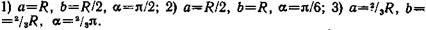
3.21. Тонкий однородный стержень длиной l =50 см и массой m =400 г вращается с угловым ускорением ε=3 рад/с2 около оси, проходящей перпендикулярно стержню через его середину. Определить вращающий момент М.
3.22. На горизонтальную ось насажены маховик и легкий шкив радиусом R=5 см. На шкив намотан шнур, к которому привязан груз массой т =0,4 кг. Опускаясь равноускоренно, груз прошел путь s=l,8 м за время t =3 с, Определить момент инерции J маховика. Массу шкива считать пренебрежимо малой.
3.23. Вал массой m =100 кг и радиусом R=5 см вращался с частотой n =8 с-1. К цилиндрической поверхности вала прижали тормозную колодку с силой F =40 H, под действием которой вал остановился через t =10 с. Определить коэффициент трения f.
|
| Рис. 3.14 |
| Рис. 3.15 |
3.24. На цилиндр намотана тонкая гибкая нерастяжимая лента, массой которой по сравнению с массой цилиндра можно пренебречь. Свободный конец ленты прикрепили к кронштейну и предоставили цилиндру опускаться под действием силы тяжести. Определить линейное ускорение а оси цилиндра, если цилиндр: 1) сплошной; 2) полый тонкостенный.
3.25. Через блок, имеющий форму диска, перекинут шнур. К концам шнура привязали грузики массой m 1=100 г и т 2=110 г. С каким ускорением а будут двигаться грузики, если масса т блока равна 400 г? Трение при вращении блока ничтожно мало.
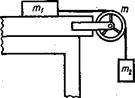
3:26. Два тела массами т 1 =0,25 кг и m 2=0,15 кг связаны тонкой нитью, переброшенной через блок (рис. 3.15). Блок укреплен на краю горизонтального стола, по поверхности которого скользит тело массой т 1. С каким ускорением а движутся тела и каковы силы T1 и Т2 натяжения нити по обе. стороны от блока? Коэффициент трения f тела о поверхность стола равен 0,2. Масса т блока равна 0,1 кг и ее можно считать равномерно распределенной по
ободу. Массой нити и трением в подшипниках оси блока пренебречь.
3.27. Через неподвижный блок массой т =0,2 кг перекинут шнур, к концам которого подвесили грузы массами m1=0,3 кг и m2=0,5 кг. Определить силы натяжения T 1 и T 2 шнура по обе стороны блока во время движения грузов, если масса блока равномерно распределена по ободу.
3.28. Шар массой m =10 кг и радиусом R =20 см вращается во
круг оси, проходящей через его центр. Уравнение вращения шара
имеет вид 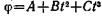 , где В=4 рад/с2, С= —1 рад/с3. Найти
, где В=4 рад/с2, С= —1 рад/с3. Найти
закон изменения момента сил, действующих на шар. Определить
момент сил М в момент времени t=2 с.
Date: 2015-07-22; view: 1393; Нарушение авторских прав
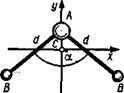
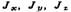 трехатомных мо- лекул типа АВ2 относительно осей х, у, z (рис. 3.8), проходящих через центр инерции С молекулы (ось z перпендикулярна плоско- сти ху). Межъядерное расстояние А В обозначено d, валентный угол а. Вычисления выполнить для следующих молекул: 1) H2O (d = =0,097 нм,
трехатомных мо- лекул типа АВ2 относительно осей х, у, z (рис. 3.8), проходящих через центр инерции С молекулы (ось z перпендикулярна плоско- сти ху). Межъядерное расстояние А В обозначено d, валентный угол а. Вычисления выполнить для следующих молекул: 1) H2O (d = =0,097 нм, 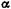 = 104°30'); 2) SO2(d =0,145нм,
= 104°30'); 2) SO2(d =0,145нм, 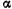 =124°).
3.6.Определить момент инерции J тонкого однородного стержня длиной l =30 см и массой m =100 г относительно оси, перпендику-
=124°).
3.6.Определить момент инерции J тонкого однородного стержня длиной l =30 см и массой m =100 г относительно оси, перпендику-