Методика измерений. Для выполнения работы, связанной непосредственно с моделированием распределения Максвелла, используется кювета

Для выполнения работы, связанной непосредственно с моделированием распределения Максвелла, используется кювета, имеющая узкое отверстие на прозрачной стенке и два круглых отверстия разного диаметра на выпуклой части (рис. 2.4). Если поднять регулятор 5, то шарики, вылетевшие из прибора 1, попадут в кювету через верхнее отверстие и затем, миновав узкое отверстие на ее прозрачной стенке, окажутся в отсеках верхнего приемника 8. Нижнее отверстие меньшего диаметра служит для того, чтобы шарики, вылетевшие из прибора 1, но имеющие недостаточную скорость, попали обратно во внутреннюю камеру.

Рис. 2.4 Кювета, используемая при моделировании распределения Максвелла

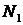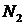Число шариков , попавших в первый отсек, имитирует число молекул, скорости которых имеют значения от до . Число шариков , попавших во второй отсек, имитирует число молекул со скоростями от до 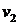и т. д. Обозначим общее число шариков 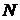. Отношение 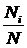есть вероятность 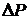того, что молекулы модельного газа имеют скорости в интервале .

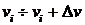Экспериментальные результаты (количество шаров с разной скоростью) можно в соответствии с (3) представить в виде графика функции:

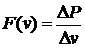, (34)

где 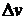– изменение скорости, соответствующее изменению пути на 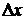(длина одной ячейки верхнего приемника) и определяемое как

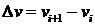, (35)

Скорость шарика, попавшего в 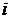-й отсек, можно найти, зная его дальность полета 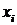(если шарик вылетает из отверстия установки горизонтально):

, (36)

где 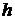- это разница высот между выходным отверстием на кювете и основанием верхнего приемника шариков. Коэффициент 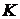в эксперименте есть величина постоянная и для упрощения выполнения работы может быть рассчитан отдельно.

Зная общее количество шариков 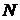в ячейках, количество шариков в каждом отсеке 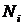и среднее значение скорости для данного отсека 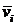, можно найти среднюю арифметическую скорость движения шариков

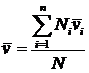, (37)

где n – число заполненных отсеков.

Средняя квадратичная скорость находится из условия

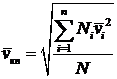. (38)

Ячейка с максимальным количеством попавших в нее шариков 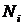будет соответствовать наиболее вероятной скорости 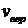. Таким образом, зная характерные скорости, можно будет проверить соотношение (32), а также сравнить теоретический вид распределения Максвелла с полученным экспериментально.

Date: 2015-07-23; view: 497; Нарушение авторских прав