Краткие сведения из теории вероятностей

О вероятности. Основу статистической физики составляет теория вероятностей. Вероятность интересующего нас события характеризуется кратностью его повторения. Если в 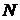случаях 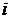-е событие происходит 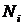раз, то вероятностью 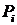этого события называют величину

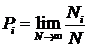. (1)

На практике 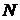всегда конечно, поэтому для вычисления вероятности стараются, чтобы 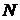и 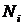были достаточно большими. Тогда можно считать, что

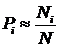­ . (2)

Ясно, что сумма вероятностей всех возможных результатов измерений равна единице:

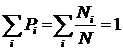. (3)

Теперь обратимся к вычислению сложных событий. Рассмотрим две основные теоремы: о сложении и умножении вероятностей. Проще всего это понять на примере игрального кубика.

Теорема о сложении вероятностей заключается в том, что вероятность того, что в результате 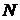бросаний кубика выпадет 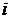или 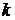, равна:

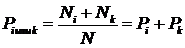. (4)

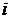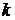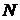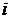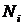Теорема об умножении вероятностей позволяет находить вероятность того, что при двух бросаниях кубика выпадет последовательно и (или наоборот). Рассмотрим двойных бросаний кубика. Пусть первое бросание из каждой пары бросков дало в случаях (так что 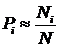). Теперь выделим из этих 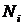случаев те случаев, когда второе бросание давало 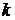(так что 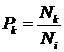). Искомая вероятность

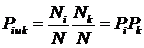. (5)

Средние значения случайных величин. Зная вероятности появления различных результатов измерения дискретной величины 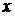, можно найти их среднее значение 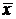. По определению среднего

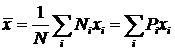. (6)

Функция распределения. Рассмотрим случай, когда случайная величина 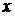имеет непрерывный характер (например, скорости молекул). Для этого разобьем всю область изменения 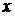на отдельные интервалы и будем считать число попаданий случайной величины в тот или иной интервал. Интервалы, во избежание заметных флуктуаций, должны быть достаточно большими – так, чтобы в каждом из них число попаданий было 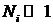и чтобы с помощью (2) можно было определить вероятность попадания случайной величины в данный интервал. Вместе с тем, интервалы должны быть достаточно небольшими, чтобы более детально характеризовать распределение величины .

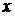Допустим, нам известна вероятность 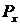попадания в тот или иной интервал 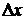. В качестве характеристики случайной величины на этот раз выступает отношение 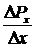, которое для достаточно малых интервалов не зависит от величины самого интервала .

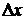Это отношение при 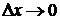называют функцией распределения 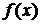случайной величины :

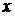. (7)

Видно, что функции распределения 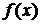можно приписать смысл плотности вероятности, т.е. вероятности интересующей нас величины оказаться в единичном интервале вблизи значения .

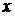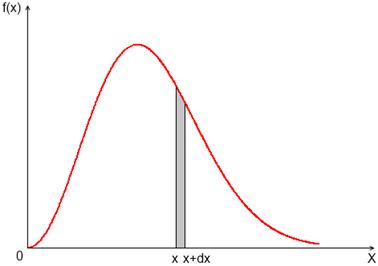
Рис. 1.1 Произвольная функция распределения случайной величины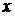

В разных случаях функция распределения имеет совершенно различный вид, один из которых в качестве примера приведен на рис. 1.1. В соответствии с (7) площадь полоски шириной 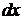на этом рисунке равна вероятности того, что случайная величина 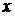окажется в пределах интервала :

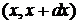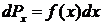. (8)

Вероятность того, что величина 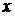попадает в произвольный интервал :

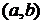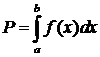. (9)

Условие нормировки. Ясно, что вероятность того, что величина 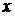может принять хотя бы какое-нибудь значение (достоверное событие), равна единице. Это и называют условием нормировки:

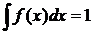, (10)

где интегрирование производится по всему интервалу возможных значений величины 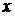. Из этого условия следует, что вся площадь под кривой 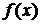(рис. 1) равна единице.

Средние значения. Среднее значение величины 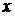можно найти, зная ее нормированную на единицу функцию распределения 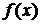. Обратимся к формуле (6). Она справедлива и для случая, когда интервал изменения величины 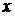будет разбит на небольшие участки. Уменьшая участки, мы должны в конце концов заменить 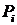на 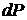и сумму 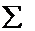– на интеграл 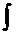. Тогда

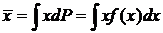, (11)

где интегрирование проводится по интересующему нас интервалу значений 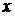. Аналогичные формулы справедливы для любой функции 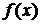, например

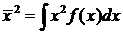. (12)

Флуктуации. Вероятность случайного события и экспериментально наблюдаемая доля результатов, когда событие осуществляется – это не одно и то же. Доля результатов испытывает случайные отклонения от предсказываемой вероятности. Отклонения такого рода происходят в любых макросистемах. Эти отклонения и обуславливают флуктуации.

Согласно теории вероятностей, относительная флуктуация любой величины изменяется в зависимости от числа испытаний 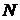по закону 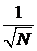. Именно огромное число 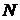молекул и объясняет, почему макроскопические законы, получаемые на основе статистических представлений о движении частиц макросистемы, оказываются точными.

Date: 2015-07-23; view: 469; Нарушение авторских прав