Распределение Максвелла

Закон распределения по скоростям молекул газа, находящегося в термодинамическом равновесии, был найден британским физиком Дж. К. Максвеллом в 1859г. Ход рассуждений Максвелла довольно сложен, поэтому полностью приводить его мы не будем, а ограничимся в основном рассмотрением подхода к решению этой проблемы.

Следует отметить, что задача о распределении молекул газа по скоростям, а также методы решения ее, приводимые дальше, являются чисто классическими. Поэтому необходимо выяснить границы применимости такого классического рассмотрения. Ответ можно получить, воспользовавшись принципом неопределенностей Гейзенберга. Выделим в газе маленький кубик со сторонами 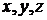, на который в среднем приходится одна частица. Если выполнены условия

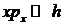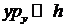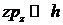, , , (13)

то движение частицы в этом кубике можно рассматривать классически. Величина

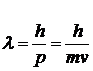(14)

имеет размерность длины. Она называется длиной волны де Бройля и играет существенную роль в квантовой механике. Перемножив три неравенства и вводя 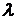, мы получим условие применимости классического рассмотрения газа

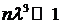, (15)

где 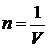– концентрация частиц внутри кубика объемом 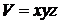. Итак, среднее число частиц в объеме 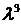должно быть мало по сравнению с единицей.

Для оценки порядка величины 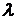воспользуемся какой-либо средней скоростью, характеризующей тепловое движение молекул газа. При обращении к молекулярно-кинетической теории газов, в нашем распоряжении оказывается средняя квадратичная скорость 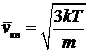. Используя ее, придадим условию (15) вид

, (16)

где введено обозначение

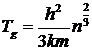(17)

Величина 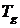называется температурой вырождения газа. Для электронного газа в серебре (и других хорошо проводящих металлах) 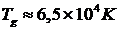, что превышает температуру плавления серебра. Отсюда следует, что электронный газ в проводящих металлах всегда вырожден. Для гелия 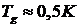(у всех остальных газов еще меньшие значения 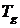). Имея столь низкие температуры вырождения, ни одно вещество не может находиться в газообразном состоянии при нормальных условиях. Именно поэтому все молекулярные газы далеки от вырождения и их можно рассматривать как классические системы.

Следуя Максвеллу, представим себе пространство скоростей с прямоугольными координатными осями, по которым будем откладывать значения проекций 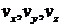отдельных молекул. Тогда скорости каждой молекулы будет соответствовать точка в этом пространстве – конец вектора 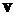. Из-за столкновений молекул положения точек будут стремительно меняться, но их распределение в целом будет оставаться неизменным, поскольку макросистема находится в термодинамическом равновесии.

Вследствие равноправности всех направлений движения расположение точек относительно начала координат будет сферически симметричным. Поэтому плотность точек может зависеть только от модуля скорости v (но не от ).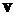

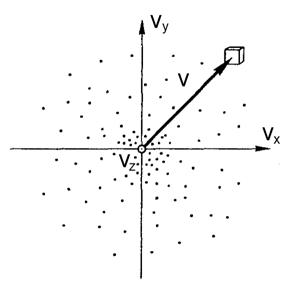
Рис. 1.2 Элементарный объем в пространстве скоростей

Итак, пусть газ содержит 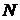молекул. Выделим в некоторой точке – конце вектора 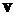– малый объем 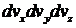(рис. 1.2). Вероятность 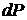того, что скорость молекулы, т.е. конец вектора 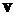, попадет в этот объем, можно записать так:

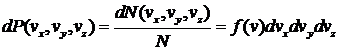, (18)

где 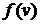имеет смысл объемной плотности вероятности.

Вероятность же того, что молекула будет иметь проекции скорости в интервале 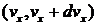, есть

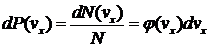, (19)

где 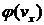– функция распределения по 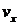. Выражение (19) – это по существу интеграл (18) по 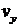и в тонком плоском слое от 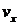до .

Считая вероятности того, что молекула имеет проекции скорости в интервалах 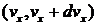, и 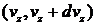независимыми, в соответствии с теоремой об умножении вероятностей можно записать

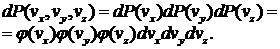(20)

Это предположение мы примем пока без обоснований. По сравнению с другими доказательствами, данными самим Максвеллом, а затем Больцманом, первое доказательство Максвелла обладает тем преимуществом, что оно не вводит никаких специальных представлений относительно структуры молекул и сил взаимодействия между ними. Поэтому оно применимо не только к газам, но и к жидкостям и к твердым телам.

Сопоставив (20) и (18), находим

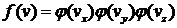. (21)

Опуская дальнейшие преобразования (с учетом условия нормировки), приведем окончательные результаты:

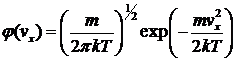, (22)

аналогичный вид имеют функци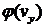и и 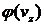. Тогда, согласно (21)

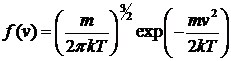. (23)

График функции 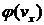изображен на рис. 1.3. Он совпадает с гауссовой кривой погрешностей. Площадь заштрихованной полоски на рис. 1.3 – это вероятность того, что проекция скорости молекулы лежит в интервале .

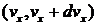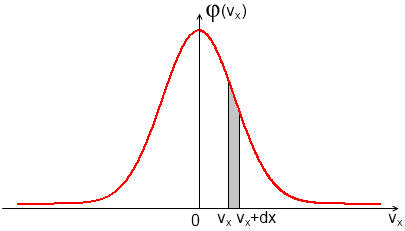
Рис. 1.3 Распределение скоростей молекул газа в проекции на ось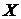

Функция (22) нормирована на единицу, т.е. площадь под кривой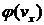

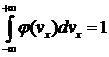. (24)

Интегрирование в пределах от 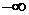до 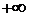не означает, что в газе есть молекулы с такими большим скоростями. Это следует рассматривать только как вычислительный прием. Молекул с весьма большими скоростями очень мало, поэтому они не вносят никакого вклада в нормировочный интеграл. Это и позволяет записывать такие пределы.

Date: 2015-07-23; view: 648; Нарушение авторских прав