Распределение молекул по модулю скорости

Найдем вероятность того, что модуль скорости молекулы попадет в интервал 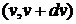. Таким молекулам соответствуют все точки, попадающие в шаровой слой с радиусам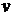и и 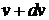(рис. 1.4). Объем этого слоя равен произведению поверхности слоя на его толщину, т.е. 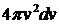, объемная же плотность вероятности 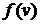во всех точках слоя одинакова. Следовательно, согласно теореме сложения вероятностей, вероятность попадания в этот слой

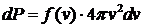. (25)

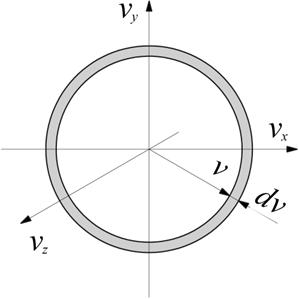
Рис. 1.4 Шаровой слой радиусов 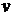и

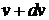
Величина 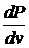– мы ее обозначим 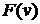– характеризует искомую вероятность, т.е. 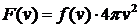. Учитывая (23), получим:

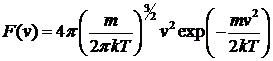. (26)

Эта формула представляет собой закон распределения Максвелла по модулю скорости. Вид функции 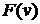приведен на рис. 1.5. Эта функция тоже нормирована на единицу:

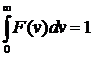. (27)

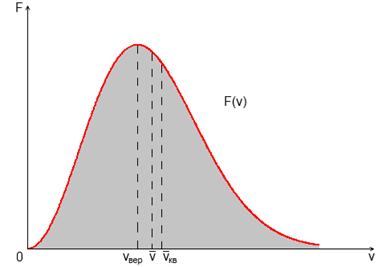
Рис. 1.5 Распределение скоростей молекул газа по модулю

Характерные скорости. К ним относятся три скорости: наиболее вероятная 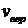, средняя 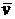и среднеквадратичная .

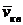Наиболее вероятной скорости соответствует максимум функции распределения 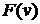. Эта скорость определяется из условия 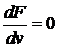, откуда следует

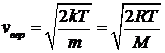. (28)

Средняя скорость по определению среднего значения случайной величины

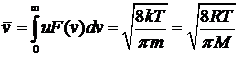. (29)

В качестве примера приведем среднюю скорость молекул азота N₂ при 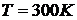: 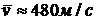. Эта величина имеет порядок скорости звука в азоте, .

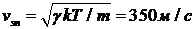Среднеквадратичная скорость 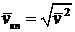; она находится из условия

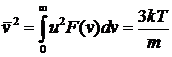, (30)

откуда

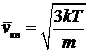. (31)

Этот результат можно получить и без интегрирования, а как следствие из выражения 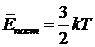для средней поступательной кинетической энергии молекулы.

Приведенные характерные скорости отличаются друг от друга в пропорции (рис. 1.5)

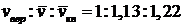. (32)

Зависимость распределения от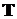

Подставив значение 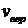из (28) в формулу (26), получим, что

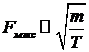. (33)

В соответствии с этим результатом для разных температур 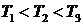кривые распределения 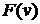будут иметь вид, показанный на рис. 1.6. Видно, что с увеличением 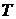максимум функции смещается в сторону больших скоростей, а его величина уменьшается согласно (33). При этом площадь под всеми тремя кривыми остается равной единице. Кривые на рис. 1.6 можно рассматривать и иначе – как соответствующие разным массам молекул газа при одной и той же температуре, причем .

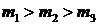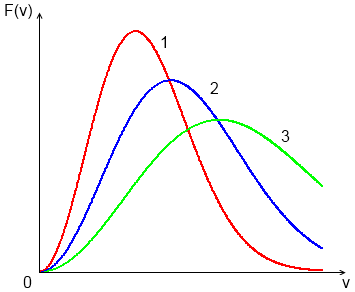
Рис. 1.6 Распределение молекул газа в зависимости от температуры.

Date: 2015-07-23; view: 746; Нарушение авторских прав