
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Модели ядер
|
|
1. А. Нейтрон и протон находятся в состояниях с |l,s,j>n = |1,1/2,3/2>, |l,s,j>p = |1,1/2,3/2>. Какие значения может иметь полный момент системы j?
Б. Два нейтрона находятся в состояниях |l,s,j>1 = |1,1/2,3/2> и |l,s,j>2 = |1,1/2,3/2>. Какие значения может иметь полный момент системы j?
В случае А нейтрон и протон не являются тождественными частицами, поэтому полный момент системы | j1 – j2 | < j < j1 + j2, то есть j = 0, 1, 2, 3.
В случае Б значения j = 1, 3 запрещены принципом Паули, т.к. в этом случае тождественные частицы будут иметь одинаковый набор квантовых чисел l, s, j, jz, что недопустимо. Поэтому j = 0, 2.
Поясним сказанное. В таблице представлены возможные значения суммарной проекции полного момента j двух фермионов с j1 = j2 = 3/2 на ось Z, то есть значения jz = (j1)z + (j2)z.
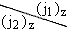
| -3/2 | -1/2 | 1/2 | 3/2 |
| -3/2 | -3 | -2 | -1 | |
| -1/2 | -2 | -1 | ||
| 1/2 | -1 | |||
| 3/2 |
Если фермионы тождественны, то они не могут иметь одинаковые наборы n, l, j, jz. Поэтому необходимо исключить все наборы jz = (j1)z + (j2)z, находящиеся на диагонали таблицы. Кроме того, два состояния, различающиеся обменом (j1)z и (j2)z, являются одним и тем же состоянием. Поэтому можно исключить jz, находящиеся ниже диагонали. Итак, приходим к следующей таблице
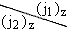
| -3/2 | -1/2 | 1/2 | 3/2 |
| -3/2 | -2 | -1 | ||
| -1/2 | ||||
| 1/2 | ||||
| 3/2 |
Набор jz = -2, -1, 0, 1, 2 соответствует j = 2. Оставшееся значение jz = 0 соответствует j = 0. Таким образом, для тождественных фермионов остаются j = 0 и 2.
2. Сравнив экспериментально измеренное значение магнитного момента дейтрона 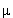 =0.86
=0.86 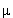 N с магнитным моментом системы нейтрон-протон в состоянии с j = 1 и относительным орбитальным моментом L = 0 (S1-состояние), оценить вклад компоненты с j = 1 и L = 2 (D1-состояние) в волновую функцию дейтрона.
N с магнитным моментом системы нейтрон-протон в состоянии с j = 1 и относительным орбитальным моментом L = 0 (S1-состояние), оценить вклад компоненты с j = 1 и L = 2 (D1-состояние) в волновую функцию дейтрона.
Магнитные моменты ядер измеряются в ядерных магнетонах. Ядерный магнетон
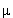 N = e N = e 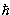 /2mpc, /2mpc,
|
где mp - масса протона.
Магнитный дипольный момент системы нуклонов 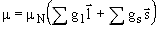 , где
, где 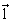 - орбитальный момент нуклона,
- орбитальный момент нуклона, 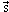 - его спин, а сумма берется по всем нуклонам системы. Безразмерные константы gl и gs называются соответственно орбитальным и спиновым гиромагнитными отношениями.
- его спин, а сумма берется по всем нуклонам системы. Безразмерные константы gl и gs называются соответственно орбитальным и спиновым гиромагнитными отношениями.
| Протон | Нейтрон | |
| gl | +1 | |
| gs | +5.586 | -3.826 |
Состояние дейтрона с j = 1 может быть представлено суперпозицией S1 и D1 состояний с относительными орбитальными моментами L = 0 и L = 2. В случае L = 0 спины протона и нейтрона параллельны, а в случае L = 2 их векторы направлены противоположно вектору орбитального момента. В этом последнем случае орбитальный момент каждого нуклона l = L/2 = 1 (см. рисунок).
Случай L = 0 (ln = lp = 0): 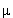 = = 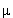 N(1 N(1  0 + 0 0 + 0 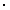 0 + 5.586 0 + 5.586 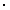 1/2 - 3.862 1/2 - 3.862 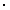 1/2) = 0,88 mN . 1/2) = 0,88 mN .
| 
|
Случай L = 2 (ln = lp = 1): 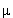 = = 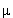 N(1 N(1 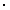 1 + 0 1 + 0 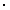 1 – 5.586 1 – 5.586 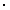 1/2 + 3.862 1/2 + 3.862  1/2) = 0,12 1/2) = 0,12 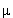 N. N.
| 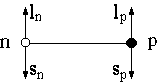
|
Обозначим вклад состояния с L = 2 как X. Тогда X 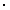 0,12
0,12 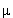 N + (1 – X)
N + (1 – X) 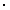 0,88
0,88 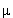 N = 0,86
N = 0,86 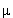 N. Получаем X = 0.026. То есть вклад состояния с L = 2 в волновую функцию дейтрона составляет 2,6%.
N. Получаем X = 0.026. То есть вклад состояния с L = 2 в волновую функцию дейтрона составляет 2,6%.
3. Известно, что внутренний электрический квадрупольный момент Q0 ядра 175Lu равен +5.9 Фм2. Какую форму имеет это ядро? Чему равен параметр деформации этого ядра?
Для равномерно заряженного аксиально симметричного эллипсоида, имеющего заряд Ze Q0 = 2Z(b2 - a2)/5, где b - полуось эллипсоида, направленная по оси симметрии Z, a a - по осям X и Y. Параметр деформации ядра
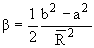 , ,
|
где 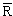 = (b + a)/2 - средний радиус ядра. Тогда
= (b + a)/2 - средний радиус ядра. Тогда
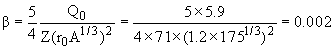 . .
|
Здесь учтено, что при малых деформациях 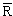
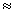 R = r0A1/3. Так как Q0 > 0, то b > a, и ядро представляет из себя эллипсоид вытянутый вдоль оси симметрии Z.
R = r0A1/3. Так как Q0 > 0, то b > a, и ядро представляет из себя эллипсоид вытянутый вдоль оси симметрии Z.
4. Внешний наблюдаемый квадрупольный момент ядра 85Rb Q = 0.7 б. Определить собственный квадрупольный момент ядра Q0, если спин ядра 85Rb равен J = 5/2.
Внешний наблюдаемый электрический квадрупольный момент ядра в лабораторной системе координат Q связан с собственным квадрупольным моментом ядра Q0 соотношением

где J - спин ядра. Отсюда
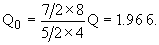
5. Определить значения изоспинов I основных состояний ядер изотопов углерода 10C, 11C, 12C, 13C, 14C.
В основном состоянии ядра значение изоспина I совпадает с модулем проекции изоспина I = | Iz |. Проекция изоспина Iz ядра, состоящего из Z протонов и N нейтронов, равна
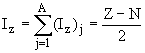 . .
|
То есть для основных состояний ядер I = |Z - N|/2.
Для указанных ядер значение изоспина будет:
для 10C - I = (6 – 4)/2 = 1,
для 11C - I = (6 – 5)/2 = 1/2,
для 12C - I = (6 – 6)/2 = 0,
для 13C - I = (7 – 6)/2 = 1/2,
для 14C - I = (8 – 6)/2 = 1.
6. Рассчитать расстояние между уровнями 1s, 2s и 3s ядра 90Zr для прямоугольной потенциальной ямы бесконечной глубины и ямы гармонического осциллятора.
В прямоугольной яме энергии уровней с l = 0 определяются соотношением:
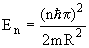 , ,
|
где n - главное квантовое число, m - масса нуклона и R - радиус ядра (ширина ямы). Величина расстояний между уровнями 1s, 2s и 3s будет
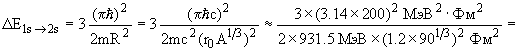
= 3 x 7.3 МэВ = 22 МэВ
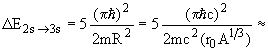
5 x 7.3 МэВ = 36.5 МэВ
В яме гармонического осциллятора выражение для энергии уровней с l = 0 определяется соотношением
En = 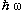 (2n + 3/2), где
(2n + 3/2), где 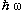 = 41 A1/3 = 41 x 901/3 = 9.1 МэВ для 90Zr.
= 41 A1/3 = 41 x 901/3 = 9.1 МэВ для 90Zr.
Расстояние будет 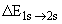 =
= 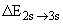 = 2
= 2 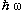 = 18.2 МэВ.
= 18.2 МэВ.
7. На основании одночастичной модели оболочек определить значения спинов и четностей J P основных состояний изотопов кислорода - 15O, 16O, 17O, 18O.
Изотопы 16O и 18O четно-четные, то есть имеют в основном состоянии спин и четность JP = 0+. Спин и четность ядра 15O определяются "нейтронной дыркой" (по отношению к четно-четному ядру 16O) в состоянии 1p1/2. Спин ядра J равен полному моменту "нейтронной дырки" в этом состоянии J = 1/2, а четность определяется орбитальным моментом l нуклона в данном состоянии P = (-1)l = (-1)1 = -1, то есть JP = 1/2-. Спин и четность ядра 17O определяется одним нейтроном в состоянии 1d5/2 сверх четно-четного остова ядра 16O. Для ядра 17O JP = 5/2+.
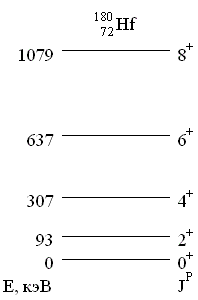
|
8. Показать, что спектр возбужденных состояний деформированного ядра 180Hf представляет собой "вращательную полосу".
Для четно-четных деформированных ядер энергия вращательных состояний
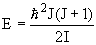 ,
,
где J - спин состояния, который принимает лишь четные значения J = 0, 2, 4, …, I - момент инерции ядра. Отношение энергий уровней должно быть следующим:
E2: E4: E6: E8 = J2(J2 + 1): J4(J4 + 1): J6(J6 + 1): J8(J8 + 1) = = 2(2 + 1): 4 (4 + 1): 6(6 + 1): 8 (8 + 1) = 3: 10: 21: 36.
Подставим приведенные на рисунке значения энергий и получим:
E2: E4: E6: E8 = 93: 307: 637:1079 = 93/31: 307/31: 637/31: 1079/31 = 3: 9.90: 20.55: 34.81.
Полученные отношения, а также отсутствие в спектре в спектре уровней с J = 1, 3, 5, … указывают, что это "вращательная полоса" ядра.
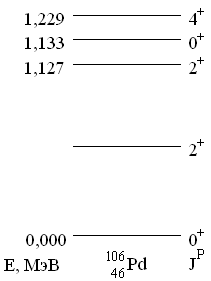
|
9. На схеме показан спектр возбужденных состояний ядра 106Pd. Оценить энергию первого возбужденного состояния 2+.
Это типичный спектр квадрупольных колебаний сферически симметричного ядра, имеющего в основном состоянии JP = 0+. Квадрупольные колебания атомных ядер характеризуются фононом JP = 2+. Положение энергетических уровней определяется числом фононов N: EN = (N + 5/2) 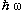 , где
, где 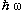 - энергия квадрупольного фонона. На рисунке есть только два уровня с JP = 2+, нижний (искомый) уровень имеет N = 1, а второй N = 2.
- энергия квадрупольного фонона. На рисунке есть только два уровня с JP = 2+, нижний (искомый) уровень имеет N = 1, а второй N = 2.
Тогда E0 = 5/2 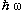 , E1 = 7/2
, E1 = 7/2 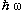 , E2 = 9/2
, E2 = 9/2 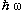 .
.
Энергия второго 2+ - состояния
E2 - E0 = (9/2 - 5/2) 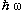 = 2
= 2 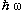 =1.127 МэВ.
=1.127 МэВ.
Энергия первого (искомого) 2+-состояния
E1 - E0 = (7/2 - 5/2) 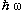 =
= 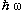 = 0.564 МэВ.
= 0.564 МэВ.
Для спектра квадрупольных колебаний четно-четных ядер имеющих в основном состоянии характерными особенностями являются следующие:
- Первое возбужденноое состояние имеет JP = 2+.
- При энергиях возбуждения, вдвое превышающих энергию первого возбужденного состояния должны находятся три состояния с примерно одинаковой энергией и имеющих квантовые характеристики JP = 0+, 2+, 4+, что соответствует сумме двух квадрупольных фононов 2+.
Date: 2015-07-23; view: 634; Нарушение авторских прав