
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Из выражения (2.5.2) имеем
|
|
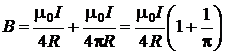 .
.
Проверим размерность:
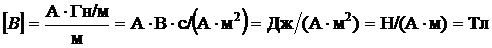 .
.
Подставив значения, получаем: 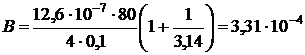 Тл.
Тл.
ОТВЕТ: 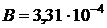 Тл.
Тл.
ЗАДАЧА 2. Тонкая лента шириной 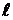 свернута в трубку радиусом R (рис.2.5.2). По ленте течет равномерно распределенный по ее ширине ток I. Определить модуль вектора магнитной индукции в произвольной точке на оси трубки.
свернута в трубку радиусом R (рис.2.5.2). По ленте течет равномерно распределенный по ее ширине ток I. Определить модуль вектора магнитной индукции в произвольной точке на оси трубки.
ДАНО:
 R
I
R
I
|
| B –? |
АНАЛИЗ. Для решения данной задачи воспользуемся принципом суперпозиции магнитных полей. Рассматриваемый проводник нельзя считать линейным током, поэтому непосредственно применять закон Био-Савара-Лапласа нельзя. Разделим трубку на узкие кольца шириной dy. Рассмотрим кольцо, расположенное на расстоянии y от произвольной точки A 1 на оси трубки. Такое кольцо можно считать тонким круговым током с силой тока dI
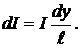
Этот круговой ток создает в точке А 1 магнитную индукцию
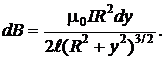 (2.5.3)
(2.5.3)
Все элементы 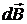 имеют одинаковое направление против оси Y, поэтому индукция, создаваемая в точке А 1 всей трубкой, равна
имеют одинаковое направление против оси Y, поэтому индукция, создаваемая в точке А 1 всей трубкой, равна
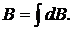 (2.5.4)
(2.5.4)
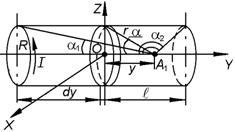
Рис. 2.5.2
РЕШЕНИЕ. Для решения интеграла (2.5.4) сделаем следующую подстановку:
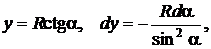
где 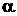 – угол, под которым радиус кольца R виден из точки А 1. Тогда
– угол, под которым радиус кольца R виден из точки А 1. Тогда
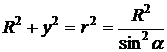 ,
,
и выражение (2.5.3) принимает вид
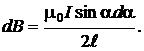
Угол 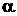 изменяется в пределах от
изменяется в пределах от 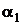 до
до 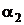 ,
, 
 где b – расстояние от точки А 1 до правого края ленты.
где b – расстояние от точки А 1 до правого края ленты.
Магнитная индукция в точке А 1, согласно (2.5.4), равна
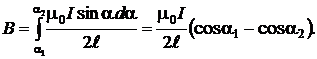
Проверим размерность:
 .
.
Рассмотрим различные частные случаи.
- Точка А 1 находится в середине трубки.
Тогда
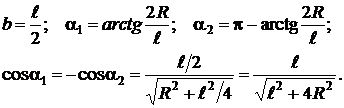
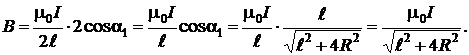
2. Т очка А 1 – в левом торце трубки.
В этом случае
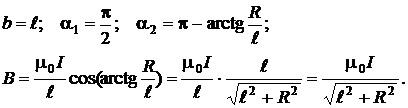
Если 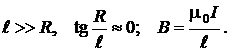
3. Точка А 1 находится в правом торце трубки
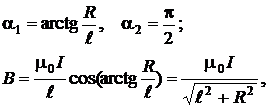
при 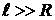
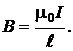
ОТВЕТ: 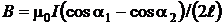 ; при
; при 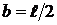
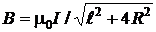 ; при
; при 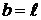
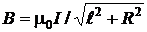 ; при
; при 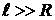
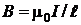 .
.
ЗАДАЧА 3. По сплошному бесконечному цилиндрическому проводнику радиусом R течет ток плотности  . Рассчитать магнитное поле внутри проводника.
. Рассчитать магнитное поле внутри проводника.
ДАНО:
R

|
| B –? |
АНАЛИЗ. Проводник нелинейный, поэтому закон Био-Савара-Лапласа применять нельзя. Воспользуемся законом полного тока. Рассчитаем поле в точке А (рис. 2.5.3), находящейся на расстоянии r от центра проводника. Проведем окружность радиусом r с центром в точке О на оси проводника. В силу симметрии модуль вектора 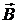 в каждой точке окружности одинаков. Ток, охватываемый этой окружностью, равен
в каждой точке окружности одинаков. Ток, охватываемый этой окружностью, равен
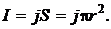
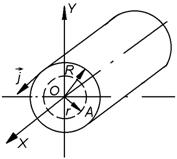 Рис. 2.5.3
Рис. 2.5.3
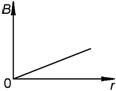 Рис. 2.5.4
Рис. 2.5.4
|
По закону полного тока (теореме о циркуляции вектора 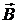 ) для вакуума
) для вакуума
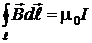 .
.
РЕШЕНИЕ. Проинтегрировав и подставив выражение для тока имеем: 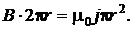 Отсюда
Отсюда 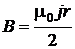 – индукция поля внутри цилиндрического проводника с током прямо пропорциональна расстоянию от оси проводника. График зависимости В (r) представлен на рис. 2.5.4.
– индукция поля внутри цилиндрического проводника с током прямо пропорциональна расстоянию от оси проводника. График зависимости В (r) представлен на рис. 2.5.4.
Проверим размерность:
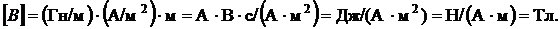
ОТВЕТ: 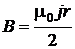 .
.
ЗАДАЧА 4. Замкнутый тороид имеет N = 400 витков из тонкого провода, намотанных в один слой. Средний диаметр тороида d = 25 см. Определить напряженность и индукцию магнитного поля внутри тороида, если сила тока
I = 0,5 А.
| ДАНО: N = 400 d =0,25 м I = 0,5 А |
| B –? H –? |
АНАЛИЗ. Для определения напряженности магнитного поля тороида воспользуемся законом полного тока (теоремой о циркуляции), так как проводники, создающие поле (тороид), обладают симметрией.
РЕШЕНИЕ. Применяя теорему о циркуляции вектора 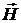 вдоль окружности диаметром d, имеем
вдоль окружности диаметром d, имеем
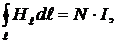
причём H = const, H l = H, поэтому 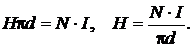
Правильность формулы по размерности очевидна. Подставив значения, получаем: 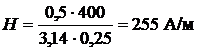 .
.
Индукция 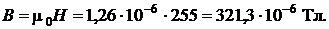
ОТВЕТ: 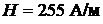 ;
; 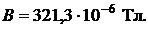
ЗАДАЧА 5. При каком соотношении между длиной 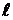 и диаметром d соленоида поле в центре его можно рассчитывать по формуле бесконечно длинного соленоида, чтобы ошибка расчета не превышала 1 %?
и диаметром d соленоида поле в центре его можно рассчитывать по формуле бесконечно длинного соленоида, чтобы ошибка расчета не превышала 1 %?
ДАНО:
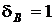 % %
|
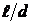 –? –?
|
АНАЛИЗ. Для решения задачи воспользуемся известными формулами для магнитного поля бесконечного соленоида и соленоида конечных размеров и на их основе выведем необходимое соотношение.
РЕШЕНИЕ. Индукция в центре бесконечно длинного соленоида в вакууме 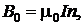
в центре конечного соленоида 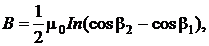
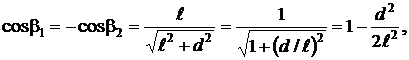
если 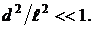 Тогда
Тогда 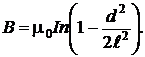
По условию задачи 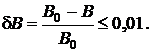
Поэтому 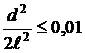 .
.
Отсюда 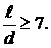
Правильность формулы по размерности очевидна.
ОТВЕТ: 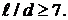
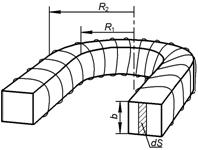
ЗАДАЧА 6. На соленоид с полым картонным сердечником в виде тора с прямоугольным поперечным сечением, размеры которого показаны на рис.2.5.5, навита обмотка из N = 500 витков, по которой течет ток 2,4 А. Определить максимальное и минимальное значения индукции магнитного поля внутри тороида и магнитный поток системы.
| ДАНО: b = 0,05 м R 1 = 0,05 м R 2 = 0,08 м N = 500 I = 2,4 А |
| Bmax –? Bmin –? Ф –? |
АНАЛИЗ. Линии индукции внутри тороида представляют собой окружности, концентричные тороиду.
Благодаря этому индукцию можно найти с помощью закона полного тока для вакуума 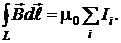
Для нахождения магнитного потока площадь поперечного сечения тороида надо разбить на узкие элементарные площадки длиной b и толщиной dr, в пределах которых поле можно считать однородным.
Тогда поток dФ через площадку dS = bdr определится выражением
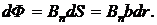 (2.5.5)
(2.5.5)
РЕШЕНИЕ. Проведём контур интегрирования  в виде окружности радиусом r, с центром на оси тороида. Направление обхода контура выберем так, чтобы во всех точках контура угол между векторами
в виде окружности радиусом r, с центром на оси тороида. Направление обхода контура выберем так, чтобы во всех точках контура угол между векторами 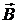 и
и 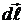 тождественно был равен нулю и
тождественно был равен нулю и 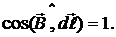
Абсолютное значение вектора 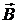 во всех точках контура будет постоянным
во всех точках контура будет постоянным
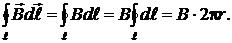
Сумма токов, сцепленных с контуром 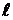 , равна произведению силы тока в обмотке на число витков N, т. е.
, равна произведению силы тока в обмотке на число витков N, т. е.
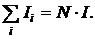
Тогда закон полного тока для поля данного тора примет вид:  т. е.
т. е. 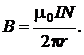
Правильность формулы по размерности очевидна.
Поле внутри тороида неоднородно, наибольшего значения индукдия В достигает при r = R 1, наименьшего – при r = R 2.
Таким образом, 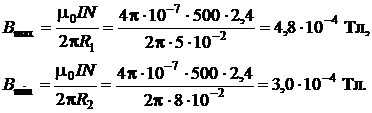
Вектор 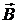 направлен по нормали к площадке dS и
направлен по нормали к площадке dS и 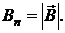
Полный магнитный поток системы найдем, интегрируя (2.5.5).
Из (2.5.5) получаем: 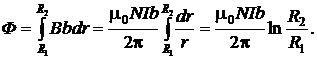
Проверим размерность: 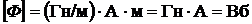 .
.
Подставив значения, получаем: 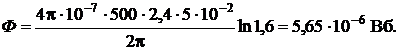
ОТВЕТ: 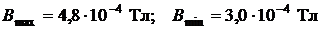 ;
; 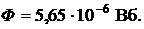
ЗАДАЧА 7. Провод в виде тонкого полукольца радиусом R = 10 см находится в однородном магнитном поле с индукцией В = 50мТл. По проводу течет ток I = 10 А. Найти силу F, действующую на провод, если плоскость полукольца перпендикулярна линиям магнитной индукции, а подводящие провода находятся вне поля.
| ДАНО: R = 0,1 м B = 50×10–3 Тл I = 10 А |
| F –? |
АНАЛИЗ. Задача на закон Ампера. Провод нелинейный, поэтому пользоваться выражением для силы Ампера 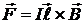 нельзя.
нельзя.
Расположим провод в плоскости чертежа перпендикулярно линиям магнитной индукции 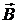 (рис. 2.5.6) и выделим на нем малый элемент
(рис. 2.5.6) и выделим на нем малый элемент 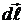 с током. Вектор
с током. Вектор 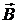 направлен перпендикулярно плоскости чертежа (за чертеж). На элемент действует сила Ампера
направлен перпендикулярно плоскости чертежа (за чертеж). На элемент действует сила Ампера
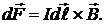
Сложив элементарные векторы 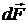 (проинтегрировав), найдем результирующую силу, действующую на полукольцо.
(проинтегрировав), найдем результирующую силу, действующую на полукольцо.
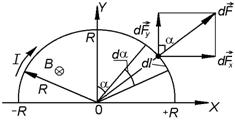
Рис. 2.5.6
РЕШЕНИЕ. Согласно правилу векторного произведения, вектор 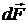 направлен перпендикулярно к
направлен перпендикулярно к 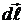 и
и 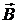 и лежит в плоскости чертежа. Разложим этот вектор на две составляющие:
и лежит в плоскости чертежа. Разложим этот вектор на две составляющие:
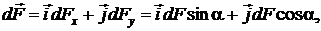 (2.5.6)
(2.5.6)
где 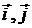 – орты координатных осей X, Y;
– орты координатных осей X, Y; 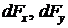 – проекции силы
– проекции силы 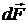 на эти оси,
на эти оси, 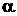 – угол между направлением силы
– угол между направлением силы 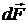 и осью Y.
и осью Y.
Модуль вектора 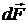 равен
равен 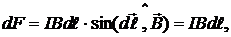
т. к. 
Силу, действующую на весь проводник, найдём, интегрируя выражение (2.5.6)
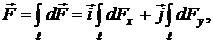
где 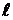 – длина проводника.
– длина проводника.
Составляющие сил, действующих на обе половинки проводника по оси Х, равны по величине и противоположны по направлению, поэтому 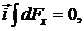
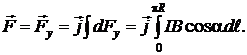
Выразим элемент дуги 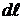 через приращение угла
через приращение угла 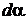 на этом элементе
на этом элементе 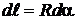 .
.
Тогда сила 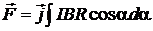 .
.
Угол 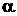 меняется от
меняется от 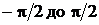 (см. рис. 2.5.6), поэтому
(см. рис. 2.5.6), поэтому
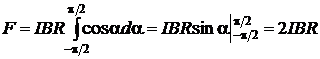 .
.
Правильность формулы по размерности очевидна.
Подставив значения, получаем: 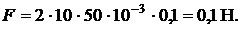
ОТВЕТ: 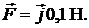
ЗАДАЧА 8. В одной плоскости с бесконечно длинным прямым током I = 5 А расположена прямоугольная рамка, обтекаемая током i = 1 А. Найти силы, действующие на каждую сторону рамки со стороны поля, создаваемого прямым током, если длинная сторона b = 20 см параллельна прямому току и находится на расстоянии x 0 = 5 см от него, а короткая сторона a = 10 см (рис.2.5.7).
| ДАНО: I = 5 A i = 1 A b = 0,20 м x 0 = 0,05 м а = 0,10 м |
| F 1; F 2; F 3; F 4 –? |
АНАЛИЗ. Задача на закон Ампера. Магнитное поле, создаваемое прямым бесконечно длинным проводником с током, действует на все элементы рамки с током по- разному.
Все элементы стороны bc рамки находятся от проводника на одинаковом расстоянии х 0, поэтому в пределах этой стороны магнитное поле проводника одинаково и для определения силы Ампера можно воспользоваться фомулой 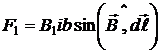 , где
, где 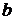 – длина стороны bc;
– длина стороны bc; 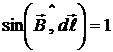 , т. к. проводник лежит в плоскости, перпендикулярной
, т. к. проводник лежит в плоскости, перпендикулярной 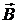 . Аналогично, для стороны
. Аналогично, для стороны 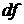
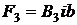 . Направления сил
. Направления сил 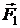 и
и  определяются по правилу левой руки и показаны на рис. 2.5.7, причем
определяются по правилу левой руки и показаны на рис. 2.5.7, причем 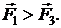
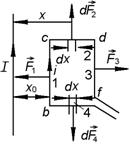 Рис. 2.5.7
Рис. 2.5.7
|
Вдоль сторон рамки cd (2) и bf (4) индукция поля 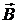 непрерывно меняется. Выделим элемент проводника dx стороны сd, находящийся на расстоянии x от прямого тока (рис. 2.5.7). Сила, действующая на этот элемент, равна
непрерывно меняется. Выделим элемент проводника dx стороны сd, находящийся на расстоянии x от прямого тока (рис. 2.5.7). Сила, действующая на этот элемент, равна
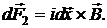
Направление силы определяется векторным произведением 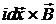 , т. е. сила направлена вверх. Модуль ее по закону Ампера равен
, т. е. сила направлена вверх. Модуль ее по закону Ампера равен
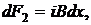 (2.5.7)
(2.5.7)
т. к. 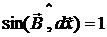 .
.
Сила 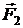 , действующая на сторону рамки cd, определяется интегралом
, действующая на сторону рамки cd, определяется интегралом
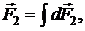
При переходе от одного элемента стороны cd к другому направление элементарных сил 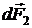
 не меняется, поэтому можно перейти к скалярной форме записи
не меняется, поэтому можно перейти к скалярной форме записи 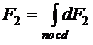 . (2.5.8)
. (2.5.8)
РЕШЕНИЕ. Бесконечно длинный прямой ток I создает в вакууме магнитное поле, индукция которого
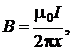 (2.5.9)
(2.5.9)
где х – расстояние от прямого тока до точки, в которой рассматривается поле.
Для определения сил 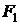 и
и 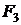 подставим (2.5.9) в закон Ампера, имеем
подставим (2.5.9) в закон Ампера, имеем 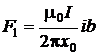 и
и 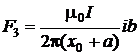 .
.
Проверим размерность: 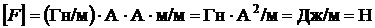 .
.
Подставив значения, получаем: 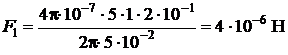 ,
,
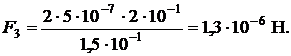
Для определения сил 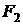 и
и 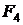 подставим в (2.5.8) выражения (2.5.9) и (2.5.7):
подставим в (2.5.8) выражения (2.5.9) и (2.5.7):
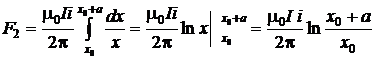 .
.
Проверим размерность: 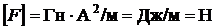 . Подставив значения, получаем:
. Подставив значения, получаем: 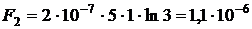 Н.
Н.
Сила 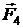 , действующая на сторону bf равна по модулю
, действующая на сторону bf равна по модулю 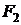 и направлена противоположно ей.
и направлена противоположно ей.
ОТВЕТ: 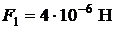 ;
; 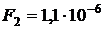 Н;
Н; 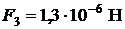 ;
; 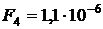 Н.
Н.
ЗАДАЧА 9. Электрон движется в магнитном поле, индукция которого 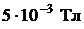 , по винтовой линии с радиусом R = 2 см и шагом «винта» h = 5 см. Определить энергию электрона в электрон-вольтах и направление вектора скорости в начальный момент времени.
, по винтовой линии с радиусом R = 2 см и шагом «винта» h = 5 см. Определить энергию электрона в электрон-вольтах и направление вектора скорости в начальный момент времени.
| ДАНО: В = 5×10-3 Тл R = 0,02 м h = 0,05 м |
WK –?
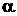 –? –?
|
АНАЛИЗ. На электрон, влетающий в магнитное поле индукции 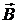 , действует сила Лоренца
, действует сила Лоренца
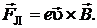 (2.5.10)
(2.5.10)
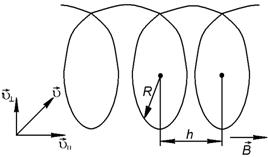 Рис. 2.5.8
Рис. 2.5.8
|
Направление этой силы в пространстве может меняться по мере изменения направления вектора 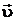 , вызванного действием этой силы, но она все время остается перпендикулярной к вектору скорости. Таким образом, под действием силы Лоренца движущийся электрон может приобретать только нормальное ускорение. Если бы электрон влетел в магнитное поле перпендикулярно линиям индукции, то он двигался бы по дуге окружности в плоскости, перпендикулярной к линиям индукции. Движение по спирали возможно, если существует составляющая скорости
, вызванного действием этой силы, но она все время остается перпендикулярной к вектору скорости. Таким образом, под действием силы Лоренца движущийся электрон может приобретать только нормальное ускорение. Если бы электрон влетел в магнитное поле перпендикулярно линиям индукции, то он двигался бы по дуге окружности в плоскости, перпендикулярной к линиям индукции. Движение по спирали возможно, если существует составляющая скорости 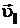 , направленная вдоль поля, не изменяющаяся ни по величине, ни по направлению. Вектор начальной скорости
, направленная вдоль поля, не изменяющаяся ни по величине, ни по направлению. Вектор начальной скорости 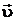 можно представить как, векторную сумму скоростей
можно представить как, векторную сумму скоростей 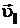 и
и 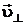 , где
, где 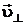 – составляющая, перпендикулярная вектору индукции;
– составляющая, перпендикулярная вектору индукции; 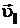 – составляющая, параллельная вектору индукции (рис. 2.5.8).
– составляющая, параллельная вектору индукции (рис. 2.5.8).
Записав уравнение динамики для электрона, находим модуль скорости, а, следовательно, и кинетическую энергию электрона.
РЕШЕНИЕ. Под действием силы Лоренца электрон приобретает только нормальное ускорение и по закону Ньютона 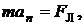
где m – масса электрона, 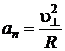 и R – радиус винтовой линии, т. е.
и R – радиус винтовой линии, т. е. 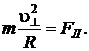
Из (2.5.10) следует, что 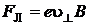 т. к.
т. к.  °. Тогда
°. Тогда 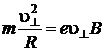 и
и
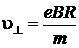 . (2.5.11)
. (2.5.11)
Шаг «винта» определится соотношением 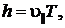 где Т – период обращения электрона по окружности, равный
где Т – период обращения электрона по окружности, равный 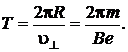
Следовательно, продольная составляющая скорости 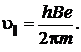 (2.5.12)
(2.5.12)
Модуль скорости 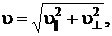
учитывая (2.5.11) и (2.5.12), имеем 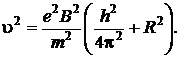
Модуль скорости: 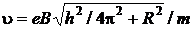 .
.
Кинетическая энергия электрона 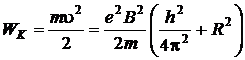 .
.
Проверим размерность:
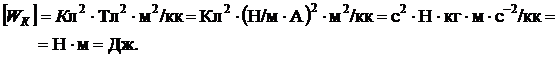
Подставив значения, получаем:
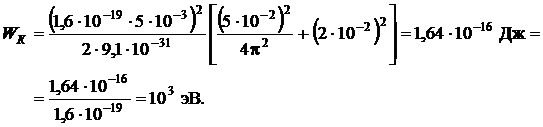
Угол 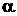 определим из соотношений
определим из соотношений
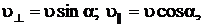 или
или 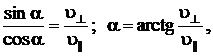
отсюда 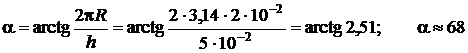 °.
°.
ОТВЕТ: 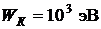 ;
; 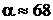 °.
°.
ЗАДАЧА 10. Квадратная рамка со стороной а = 2 см, содержащая п = 100 витков тонкого провода, подвешена на упругой нити, постоянная кручения которой С = 10 мкН.м/град. Плоскость рамки совпадает с направлением линии индукции внешнего магнитного поля. Определить индукцию внешнего магнитного поля, если при пропускании по рамке тока I = 1 А она повернулась на угол 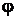 = 60°.
= 60°.
ДАНО:
а = 0,02 м
п = 100
C = 10-5 Н×м/град
I = 1 А
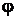 = 60° = 60°
|
| B –? |
АНАЛИЗ. Задача на динамику вращательного движения в магнитном поле. Рамка находится в равновесии, поэтому сумма моментов сил, действующих на нее, равна нулю
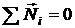 . (2.5.13)
. (2.5.13)
На рамку действуют:
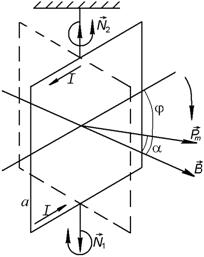 Рис. 2.5.9
Рис. 2.5.9
|
– момент сил магнитного поля с индукцией 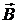 :
:
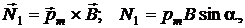 (2.5.14)
(2.5.14)
где 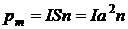 – магнитный момент рамки;
– магнитный момент рамки; 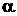 – угол между векторами
– угол между векторами 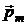 и
и 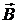 ;
;
– момент упругих сил, возникающих при закручивании нити, на которой подвешена рамка, на угол 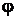 ,
, 
Подставив 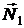 и
и 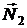 в выражение (2.5.13), получаем уравнение относительно
в выражение (2.5.13), получаем уравнение относительно 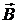 .
.
РЕШЕНИЕ. Из свойства векторного произведения (формула (2.5.14)) следует, что момент 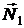 направлен по оси рамки вниз, а из условия (2.5.13) вытекает, что
направлен по оси рамки вниз, а из условия (2.5.13) вытекает, что 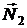 направлен противоположно
направлен противоположно 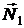 . Поэтому
. Поэтому

Из рис. 2.5.9 видно, что 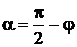 , следовательно,
, следовательно, 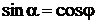 .
.
Тогда имеем
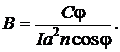
Проверим разменость: 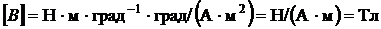 .
.
Подставляя численные значения, следует иметь в виду, что постоянная кручения С выражена не в радианах, а в градусах, поэтому 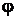 также необходимо подставить в градусах. Получаем
также необходимо подставить в градусах. Получаем
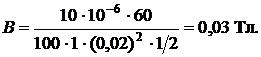
ОТВЕТ: 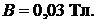
Date: 2015-07-22; view: 2143; Нарушение авторских прав