
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Прямоугольные проекции
|
|
Прямоугольная изометрическая проекция (рисунок 119). В прямоугольной изометрической проекции аксонометрические оси ОX, ОY и ОZ расположены под углом 120o друг к другу, или, что удобно для вычерчивания, составляют угол 30o с горизонтальной линией.
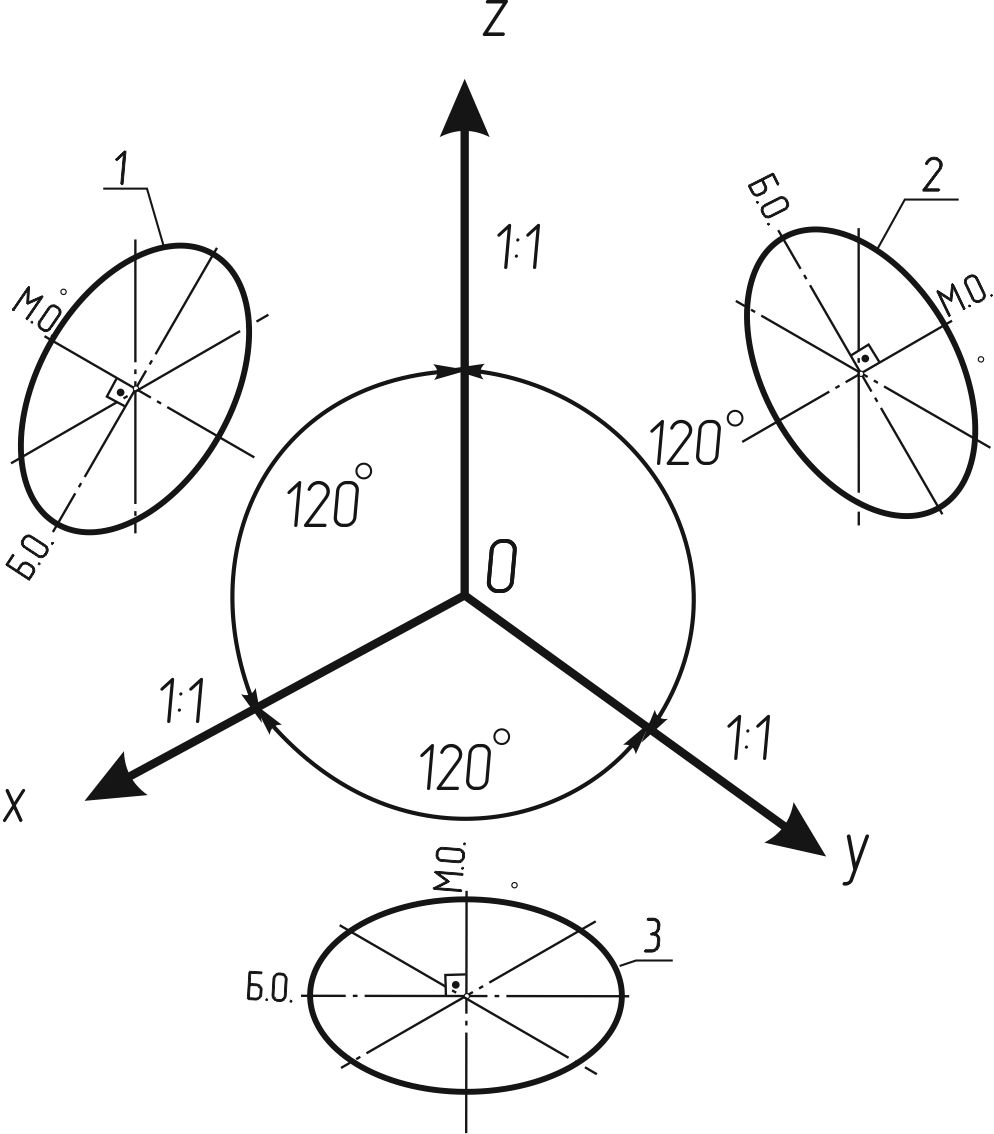
Рисунок 119
В прямоугольной аксонометрии сумма квадратов коэффициентов искажения равна двум, то есть K2x = K2y = K2z = 2.
Поэтому Kx = Ky = Kz = 0,82.
Так как эти значения неудобны для подсчета размеров при построении, то стандарт рекомендует выполнять изометрическую проекцию без искажения по осям, что соответствует замене действительных коэффициентов искажения более удобными приведенными коэффициентами, равными единице: Kx = Ky = Kz = 1. При этом изображение получается увеличенным в 1,22 раза.
Коэффициент искажения по осям OX, OY, OZ равен 0,82.
Изометрическую проекцию для упрощения, как правило, выполняют без искажения по осям OX, OY, OZ, т. е. приняв коэффициент искажения равным 1.
Окружности, лежащие в плоскостях, параллельных плоскостям проекций проецируются на аксонометрическую плоскость проекций в эллипсы (рисунок 119).
Если изометрическую проекцию выполняют без искажения по осям OX, OY, OZ, то большая ось эллипсов 1, 2, 3 равна 1,22. а малая ось — 0,71 диаметра окружности.
Если изометрическую проекцию выполняют с искажением по осям OX, OY, OZ, то большая ось эллипсов (Б.О.) 1, 2, 3 равна диаметру окружности, а малая ось (М.О.) — 0,58 диаметра окружности.
Прямоугольную изометрию применяют, когда все три видимые на аксонометрическом изображении стороны предмета имеют примерно одинаковое количество особенностей, необходимых для характеристики изображаемого предмета.
Прямоугольная диметрическая проекция (рисунок 120). В прямоугольной диметрической проекции аксонометрические оси ОX и ОZ составляют между собой угол 97o10'. Ось ОY является биссектрисой оставшегося угла, составляя с двумя другими осями равные углы 131o25' (рисунок 11). При построении этой проекции принимают, что Kx = Kz = 0,94 и Ky = 0,5Kx. =0,47.
Приведенные коэффициенты искажения будут равны: Kx = Kz = 1; Ky = 0,5, что соответствует увеличению изображения в 1,06 раза.
Окружности, лежащие и плоскостях, параллельных плоскостях проекций, проецируются на аксонометрическую плоскость проекций в эллипсы.
Если диметрическую проекцию выполняют без искажения по осям OX и OZ то большая ось эллипсов 1, 2, 3 равна 1,06 диаметра окружности, а малая ось эллипса 1 - 0,95, эллипсов 2 и 3 — 0,35 диаметра окружности.
Если диметрическую проекцию выполняют с искажением по осям OX и OZ, то большая ось эллипсов 1, 2, 3 равна диаметру окружности, а малая ось эллипса 1 — 0,9, эллипсов 2 и 3 — 0,33 диаметра окружности.
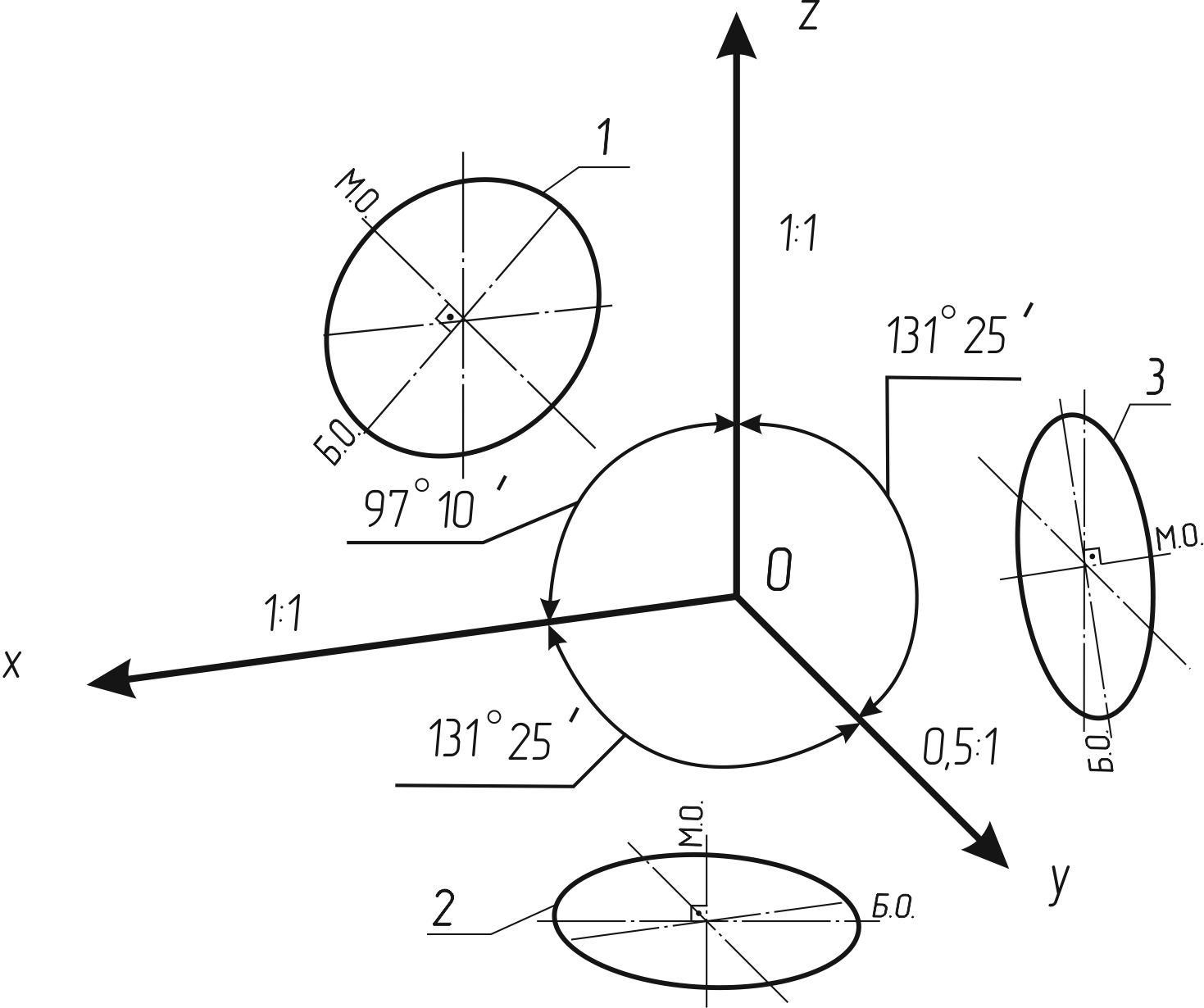
Рисунок 120
1 - эллипс (большая ось расположена под углом 90° к оси OY);
2 - эллипс (большая ось расположена под углом 90° к оси OZ);
3 - эллипс (большая ось расположена под углом 90° к оси OX)
Прямоугольная диметрия рекомендуется к применению в случае, когда наибольшее число характерных особенностей сосредоточено на одной стороне предмета. Наиболее отличающаяся особенностями сторона предмета располагается параллельно плоскости XOZ
Date: 2015-07-23; view: 629; Нарушение авторских прав