Общие положения. ГОСТ 2. 317—69 устанавливает аксонометрические проекции, применяемые в чертежах всех отраслей промышленности и строительства

ГОСТ 2.317—69 устанавливает аксонометрические проекции, применяемые в чертежах всех отраслей промышленности и строительства.

Аксонометрическая проекция — один из способов изображения пространственных фигур на плоскости. Этот вид проекций обладает большой наглядностью и является обратимым изображением. Слово “аксонометрия” в переводе с греческого означает “измерение по осям”.

Сущность способа аксонометрического проецирования показана на рисунке 117: геометрическая фигура (предмет) вместе с осями прямоугольных (декартовых) координат, к которым она отнесена в пространстве, параллельно проецируется на картинную плоскость (аксонометрическую плоскость).

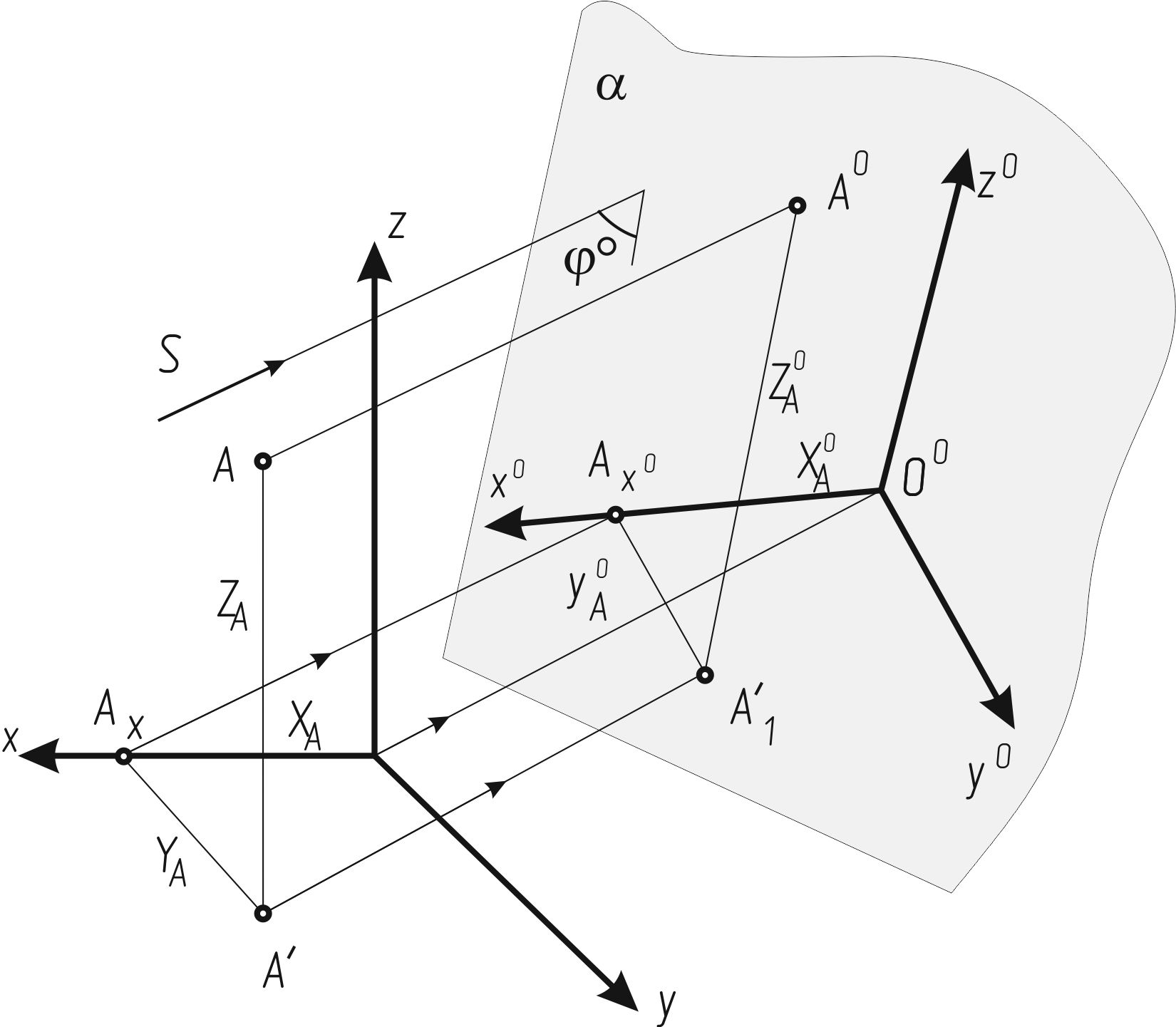
Рисунок 117

На рисунке 117 обозначено:

a — картинная (аксонометрическая) плоскость;

О_x, О_y, О_z — натуральные (декартовы) оси координат;

S — направление проецирования;

j^o — угол проецирования;

О_x, О_y, О_z — проекции натуральных осей координат на картинную плоскость — аксонометрические оси;

А^o₁ — аксонометрическая проекция точки А;

А'₁ — вторичная проекция (горизонтальная) точки А.

Для определения точки А на аксонометрической проекции (в аксонометрии) необходимо кроме аксонометрической проекции этой точки иметь ее вторичную проекцию, например, горизонтальную А₁, причем прямая А^oА'₁ должна быть параллельна аксонометрической оси z^o.

Аксонометрическая проекция точки А и ее вторичная проекция А₁ (рисунок 118) однозначно определяют положение точки в пространстве, что делает аксонометрическую проекцию обратимой. Если вторичная проекция не задана, ее можно будет задать произвольно, например, в точке А'₂, и тогда координаты X^o_A, Y^o_A, Z^o_A изменяются.

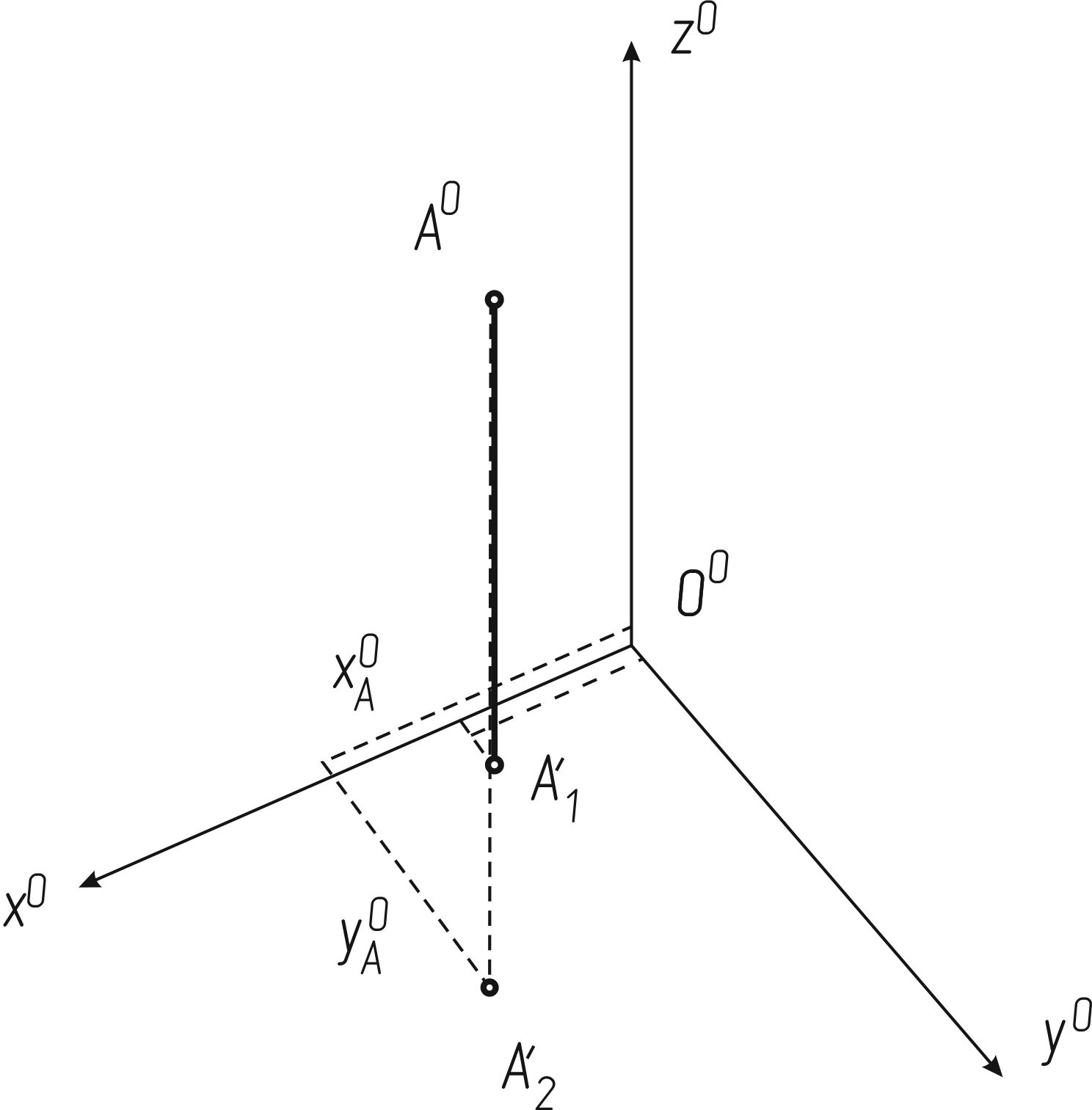
Рисунок 118

Длина отрезков натуральной координатной ломаной OA_xA'A в общем случае не равна длине их проекций О^oА^o_xА'₁А^o на картинной плоскости a (см. рисунок 117).

Искажение отрезков осей координат при их проецировании на картинную плоскость характеризуется коэффициентами искажений по аксонометрическим осям.

Коэффициентом искажения называется отношение длины аксонометрической проекции отрезка оси к его натуральной длине.

Коэффициенты искажения по осям О^oX^o, О^oY^o и О^oZ^o соответственно будут равны:

K_x = X^o_A / X_A;

K_y = Y^o_A / Y_A;

K_z = Z^o_A / Z_A.

В зависимости от направления проецирующих лучей аксонометрические проекции делятся на прямоугольные и косоугольные.

Если проецирующие прямые перпендикулярны аксонометрической плоскости проекции, то такая проекция называется прямоугольной аксонометрической проекцией. К прямоугольным аксонометрическим проекциям относятся изометрическая и диметрическая проекции.

Если проецирующие прямые направлены под углом к аксонометрической плоскости проекций, то получается косоугольная аксонометрическая проекция. К косоугольным аксонометрическим проекциям относятся фронтальная изометрическая, горизонтальная изометрическая и фронтальная диметрическая проекции.

Прямоугольные аксонометрические проекции дают наиболее наглядные изображения и поэтому чаще применяются в машиностроительном черчении.