
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Построение проекций точки на поверхности призмы по известной одной ее проекции
|
|
Пример.
Дан комплексный чертеж четырехугольной прямой призмы и фронтальная проекция А'' точки А (рисунок 130).
Прежде всего, надо отыскать на комплексном чертеже две проекции грани, на которой расположена точка А. На комплексном чертеже видно (рисунок 163, а), что точка А лежит на грани призмы 1265.
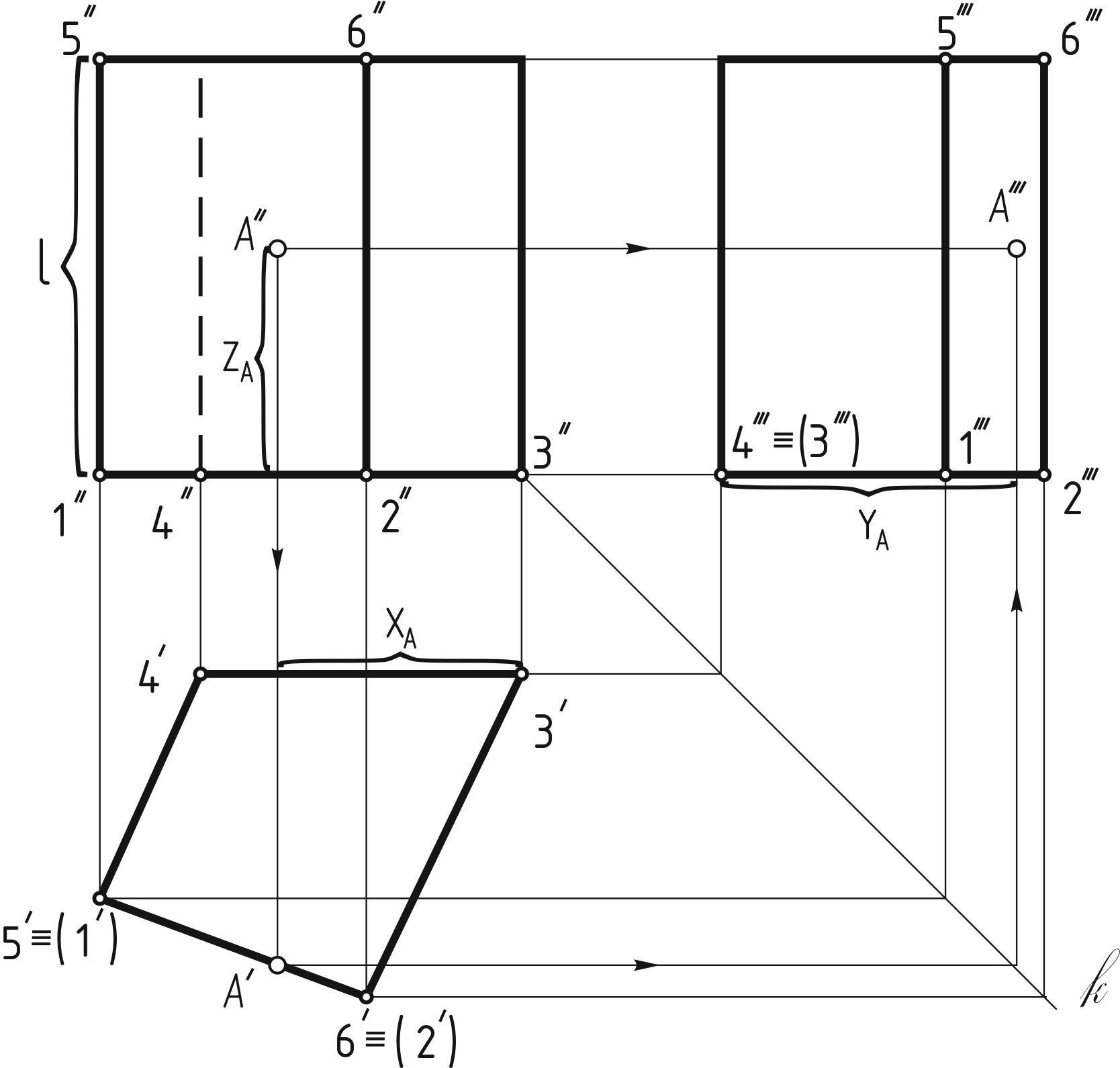
Рисунок 130
Фронтальная проекция А'' точки А лежит на фронтальной проекции 1''2''6''5'' грани призмы. Горизонтальная проекция 1'5'6'2' этой грани — отрезок 56. На этом отрезке и находится горизонтальная проекция A' точки А. Профильную проекцию призмы и точки А строят, применяя линии.
По имеющемуся комплексному чертежу призмы можно выполнить ее аксонометрию по координатам вершин. Для этого вначале строят нижнее основание призмы (рисунок 131, а), а затем - вертикальные ребра и верхнее основание (рисунок 131, б).
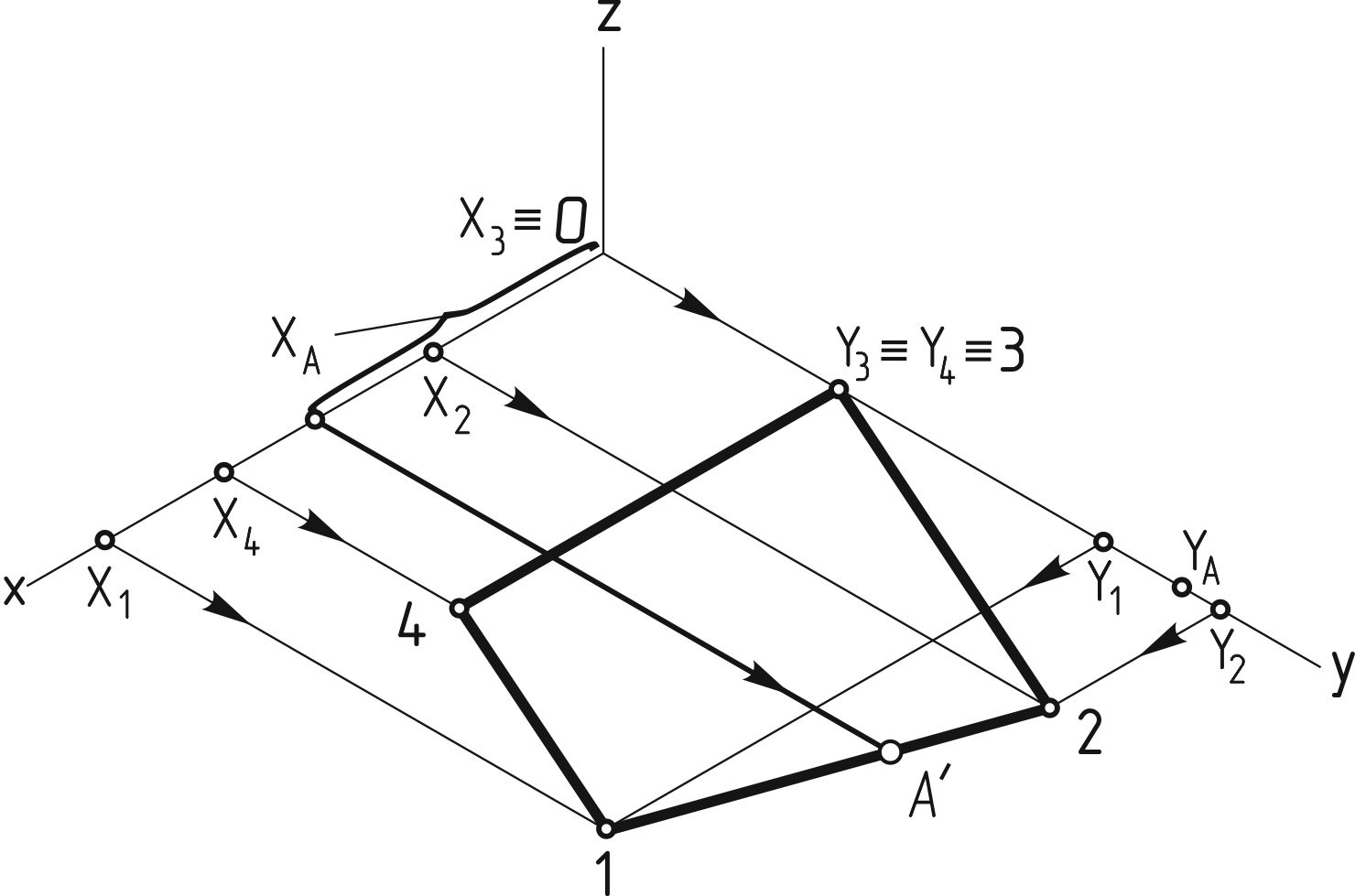
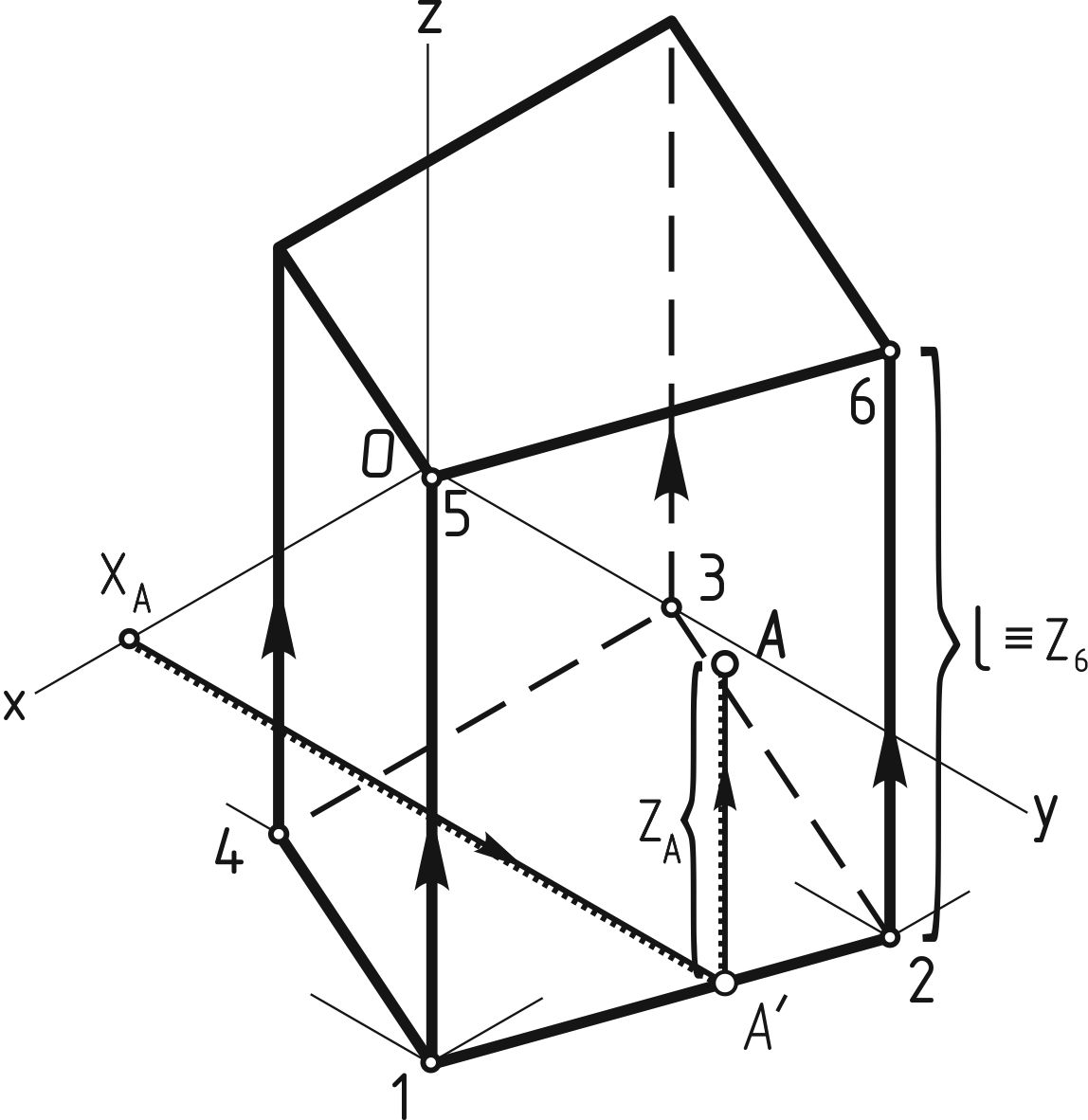
а б
Рисунок 131
По координатам точки А, взятым с комплексного чертежа, можно построить аксонометрическую проекцию этой точки.
Пирамида. Пирамидой называют многогранник (рисунок 132, а), в основании которого плоский многоугольник, а остальные грани — треугольники, имеющие общую вершину. По числу углов многоугольника основания пирамиды бывают треугольные, четырехугольные и т.д. Если пирамида усечена плоскостью, параллельной ее основанию, то ее называют усеченной (рисунок 132, б).
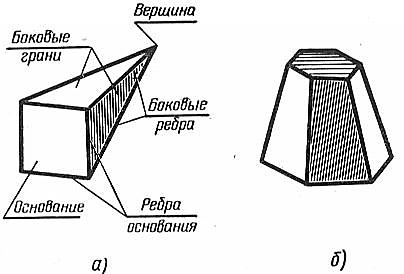
а б
Рисунок 132
Date: 2015-07-23; view: 1328; Нарушение авторских прав