
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Элементы математической статистики
|
|
Рассмотрим характеристики случайных величин на основе опытных данных.
Определение: Генеральной совокупностью называется множество всех однородных объектов, подлежащих изучению.
Определение: Выборочной совокупностью (выборкой) называется совокупность случайно отобранных однородных объектов.
Определение: Объемом совокупности называется число объектов этой совокупности.
Определение: Последовательность наблюденных значений случайного признака Х генеральной совокупности, расположенных в порядке возрастания, называется вариационным рядом:
х1,х2,……,хn, (22)
а сами значения называются вариантами, то есть хi – варианта, i=1,2,……,n.
Пусть n – объем выборки, Х – изучаемая случайная величина, которая в результате наблюдений значение хi принимает тi раз; тi называется частотой варианты хi, а отношение 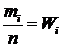 называется относительной частотой варианты, прием
называется относительной частотой варианты, прием 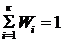 .
.
Размах выборки R – разность между максимальным и минимальным элементами выборки.
Естественной формой эмпирического закона распределения (этап обработки вариационного ряда) является статистический ряд – таблица частот, выборочный ряд – таблица относительных частот, полигон распределения, гистограмма, эмпирическая функция распределения.
Часто возникает задача нахождения подходящих приближенных значений (оценки) неизвестных параметров распределения количественного признака Х генеральной совокупности по данным выборки. Ниже рассмотрены определения статистических оценок параметров распределения: точечной и интервальной.
Определение: Точечной называют оценку неизвестного параметра распределения, которая определяется одним числом.
Выборочная средняя:
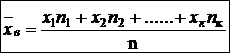 (23)
(23)
используется в качестве точечной оценки математического ожидания признака (случайной величины) Х генеральной совокупности.
Выборочная дисперсия:
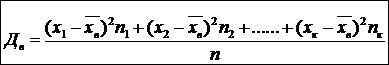 (24)
(24)
используется в качестве точечной оценки дисперсии признака Х генеральной совокупности.
Выборочное среднее квадратическое отклонение:
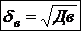 (25)
(25)
Исправленное среднее квадратическое отклонение:
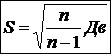 (26)
(26)
Выборочной модой М0 распределения называют варианту выборки с наибольшей частотой.
Выборочной медианой mе называют число, которое делит вариационный ряд на две части, содержащие равное число вариант.
Определение: Интервальной называют оценку неизвестного параметра, которая определяется двумя числами – концами интервала, покрывающего оцениваемый параметр.
Определение: Доверительным называют интервал, который с заданной надежностью (доверительной вероятностью) покрывает оцениваемый параметр.
Для оценки неизвестного параметра – математического ожидания а нормально распределенного количественного признака Х по выборочной средней 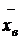 при известном среднем квадратическом отклонении σ генеральной совокупности служит доверительный интервал
при известном среднем квадратическом отклонении σ генеральной совокупности служит доверительный интервал
φγ = 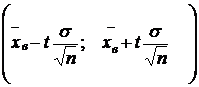 (27),
(27),
где 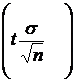 =δ – точность оценки, n – объем выборки, t – значение функции Лапласа ф(t) (таблица в приложении учебника), при котором ф(t)=
=δ – точность оценки, n – объем выборки, t – значение функции Лапласа ф(t) (таблица в приложении учебника), при котором ф(t)= 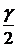 , где γ – надежность. При неизвестном σ доверительный интервал для оценки математического ожидания а имеет вид:
, где γ – надежность. При неизвестном σ доверительный интервал для оценки математического ожидания а имеет вид:
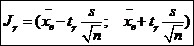 (28),
(28),
где s исправленное среднее квадратическое отклонение, tγ находится по таблице значений функции tγ=t(n,γ) по заданным n и γ (Таблица в приложении учебника).
Для оценки среднего квадратического отклонения σ нормально распределенного количественного признака Х с надежностью γ по исправленному выборочному среднему квадратическому отклонению s служат доверительные интервалы:
(S (1 -q); S (1 +q)) (при q <1) (29)
(0; S (1 +q)) (при q >1) (30),
где q находится по таблице значений функции q=q(n, γ) по заданным n и γ. (Таблица в приложении учебника).
Задача 11. Из генеральной совокупности извлечена выборка:
2,0 2,6 2,8 2,4 2,8 2,2 2,0 2,6
2,6 2,6 2,4 2,2 2,4 2,8 2,4 2,6
2,4 2,4 2,4 2,2 2,6 2,0 2,0 2,8
2,2 2,8 2,6 2,2 2,0 2,8 2,0 2,8
2,4 3,2 2,6 3,2 2,6 2,6 3,0 2,2
Признак Х имеет нормальное распределение.
Требуется: 1)Составить вариационный, статистический и выборочный ряды распределения. Найти размах выборки. По полученному распределению выборки: 2) Построить полигон относительных частот; 3) Построить график эмпирической функции распределения; 4) Вычислить выборочную среднюю, выборочную дисперсию, выборочное исправленное среднее квадратическое отклонение, моду и медиану; 5) С надежностью γ =0,95 найти доверительные интервалы для математического ожидания и среднего квадратического отклонения изучаемого признака генеральной совокупности.
Решение: 1. Вариационный ряд состоит из различных чисел: 2,0; 2,0; 2,0; 2,0; 2,0; 2,0; 2,2; 2,2; 2,2; 2,2; 2,2; 2,2; 2,4; 2,4; 2,4; 2,4; 2,4; 2,4; 2,4; 2,4; 2,6; 2,6; 2,6; 2,6; 2,6; 2,6; 2,6; 2,6; 2,6; 2,6; 2,8; 2,8; 2,8; 2,8; 2,8; 2,8; 2,8; 3,0; 3,2; 3,2.
Статистический ряд – таблица частот имеет вид: Таблица 2
| xi | 2,0 | 2,2 | 2,4 | 2,6 | 2,8 | 3,0 | 3,2 |
| ni |
В первой строке таблицы числа вариационного ряда, а во второй – их частоты.
Выборочный ряд – таблица относительных частот имеет вид:
Таблица 3
| xi | 2,0 | 2,2 | 2,4 | 2,6 | 2,8 | 3,0 | 3,2 |
| wi | 0,15 | 0,15 | 0,2 | 0,25 | 0,175 | 0,025 | 0,05 |
Размах выборки равен разности R= 3,2–2,0=1,2
2. Полигон относительных частот – графическое изображение выборочного ряда распределения. По оси абсцисс откладываются значения вариант xi, а по оси ординат значения соответствующих относительных частот wi, точки (xi, wi) соединяются отрезками прямых, образующих ломаную (рис. 5).
 |
Рис. 5. Полигон относительных частот Рис. 6. График эмпирич. функции
3. Эмпирическая функция распределения F*(x)= 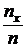 , где nx – число вариант, меньших х, n – объем выборки. Объем выборки n= 40. Наименьшая варианта равна 2,0 – следовательно при х≤ 2,0 F*(x)= 0, так как значение Х <2,0 не наблюдалось. Следующее значение варианты 2,2 – следовательно при 2,0 <х≤ 2,2 F*(x)= 0,15, так как значение Х <2,2 наблюдалось 6 раз. Проводим и далее аналогичные рассуждения. Искомая эмпирическая функция имеет вид:
, где nx – число вариант, меньших х, n – объем выборки. Объем выборки n= 40. Наименьшая варианта равна 2,0 – следовательно при х≤ 2,0 F*(x)= 0, так как значение Х <2,0 не наблюдалось. Следующее значение варианты 2,2 – следовательно при 2,0 <х≤ 2,2 F*(x)= 0,15, так как значение Х <2,2 наблюдалось 6 раз. Проводим и далее аналогичные рассуждения. Искомая эмпирическая функция имеет вид:
0 при х≤ 2,0
0,15 при 2,0 < х ≤2,2
0,3 при 2,2 < х ≤2,4
F* (x) = 0,5 при 2,4 < х ≤2,6
0,75 при 2,6 < х ≤2,8
0,925 при 2,8 < х ≤3,0
0,95 при 3,0 < х ≤3,2
1 при 3,2 < х
4. Используя формулы (23), (24), (25) определения моды и медианы находим: выборочную среднюю:
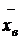 =
= 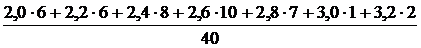 = 2,485;
= 2,485;
выборочную дисперсию:
Dв= 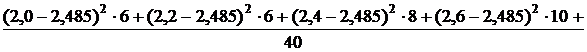
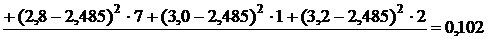 ;
;
исправленное среднее квадратическое отклонение: 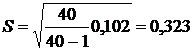 ;
;
моду: М0= 2,6; медиану: те 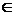 (2,4; 2,6).
(2,4; 2,6).
5.Доверительный интервал для математического ожидания имеет вид (31). Находим t= 2,023 по таблице значений функции tγ=t(γ,n) при γ= 0,95, n =40.
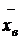 = 2,485, S =0,323, тогда уγ =(2,485-2,023
= 2,485, S =0,323, тогда уγ =(2,485-2,023 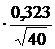 ; 2,485+2,023
; 2,485+2,023 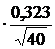 );
);
уγ =(2,382; 2,588).
Доверительный интервал для среднего квадратического отклонения имеет вид (29). Находим q= 0,24<1 по таблице значений функции q= q(γ, n) при γ= 0,95, n =40. S= 0,323, тогда γ =(0,323(1-0,24); 323(1+0,24)); γ =(0,245; 0,401).
Задача 12. Для выборки, извлеченной из генеральной совокупности, дан интервальный статистический ряд.
| αi-βi | 5-10 | 10-15 | 15-20 | 20-25 | 25-30 | 30-35 | 35-40 | 40-45 | 45-50 |
| n*i | 7 | 8 | 15 | 18 | 23 | 19 | 14 | 10 | 6 |
Требуется: 1) построить полигон интервальных относительных частот; 2)
построить кумулятивную кривую; 3) построить гистограмму относительных частот; 4) найти выборочную среднюю, выборочную дисперсию, выборочное среднее квадратическое отклонение, выборочную моду и выборочную медиану; 5) проверить на уровне значимости α=0,05 гипотезу о нормальном распределении признака Х генеральной совокупности по критерию согласия Пирсона; 6) в случае согласованности с нормальным распределением найти с надежностью γ =0,95 доверительные интервалы для оценки математического ожидания и среднего квадратического отклонения признака Х генеральной совокупности.
Решение: Объем выборки n= 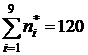 .
.
Составим таблицу 5, в которой αi-βi-i- й интервал, n  количество вариант, попадающих в i – й интервал, х
количество вариант, попадающих в i – й интервал, х 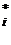 – интервальная варианта – середина интервала, х
– интервальная варианта – середина интервала, х 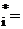
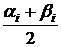 (i= 1,2, …,9), W
(i= 1,2, …,9), W 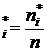 (i = 1,2, …,9) – интервальная относительная частота,
(i = 1,2, …,9) – интервальная относительная частота, 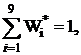
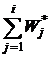 – накопленная интервальная относительная частота, ui – условная варианта.
– накопленная интервальная относительная частота, ui – условная варианта.
Таблица 5
| i | αi-βi | x 
| n 
| 
| 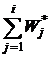
| 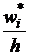
| ui | u 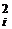
| ui n 
| u 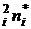
|
| 5–10 | 7,5 | 0,06 | 0,06 | 0,012 | –4 | –28 | ||||
| 10–15 | 12,5 | 0,07 | 0,13 | 0,014 | –3 | –24 | ||||
| 15–20 | 17,5 | 0,12 | 0,25 | 0,024 | –2 | –30 | ||||
| 20–25 | 22,5 | 0,15 | 0,40 | 0,030 | –1 | –18 | ||||
| 25–30 | 27,5 | 0,19 | 0,59 | 0,038 | ||||||
| 30–35 | 32,5 | 0,16 | 0,75 | 0,032 | ||||||
| 35–40 | 37,5 | 0,12 | 0,87 | 0,024 | ||||||
| 40–45 | 42,5 | 0,08 | 0,95 | 0,016 | ||||||
| 45–50 | 47,5 | 0,05 | 0,010 | |||||||
| Σ | – | – | – | – | ||||||
| Σ∕n | – | – | – | – | – | – | 0,008 | 4,358 |
1. Полигон интервальных относительных частот ломаная линия с вершинами в точках (хi*,wi i= 1,2,…,9 (рис. 7).
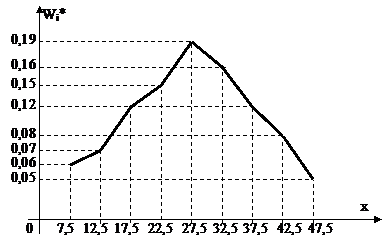
Рис. 7. Полигон интервальных относительных частот.
2. Кумулятивная кривая – ломаная линия с вершинами в точках (βi, 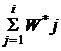 ), i= 1,2,…,9, где βi – правый конец i- го интервала группировки (рис. 8).
), i= 1,2,…,9, где βi – правый конец i- го интервала группировки (рис. 8).
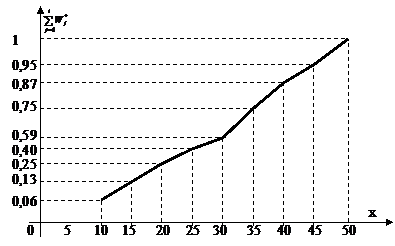
Рис. 8. Кумулятивная кривая
3. Гистограмма относительных частот – ступенчатая фигура, состоящая из прямоугольников с основаниями – интервалами (i,βi) и высотами равными 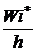 (i= 1,2,…,9)(рис. 9).
(i= 1,2,…,9)(рис. 9).
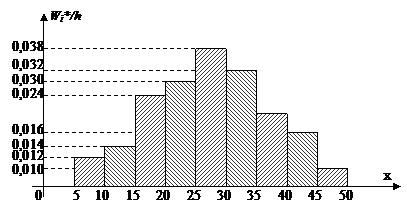
Рис. 9. Гистограмма относительных частот
4. Найдем 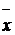 ,Dв, σв. Используем таблицу 5. Применим метод условных вариант для случая интервальной группировки. Условия варианта ui=
,Dв, σв. Используем таблицу 5. Применим метод условных вариант для случая интервальной группировки. Условия варианта ui= 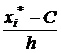 ,
, 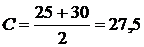 ,
, 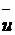 =
= 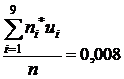 ,
, 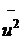 =4,358,
=4,358, 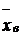 =h
=h 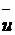 +c= 5·0,008+27,5=27,54, Dвu=
+c= 5·0,008+27,5=27,54, Dвu= 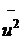 -
- 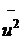 = 4,358-(0,008)2=4,358; Dвх=h2 Dвu= 52·4,358≈108,95, σвx=
= 4,358-(0,008)2=4,358; Dвх=h2 Dвu= 52·4,358≈108,95, σвx= 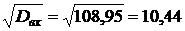 .
.
В случае интервальной группировки формула для нахождения выборочной моды имеет вид:
М0= 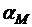 +h
+h  .
.
Формула для нахождения медианы имеет вид:
те= 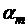 +h
+h 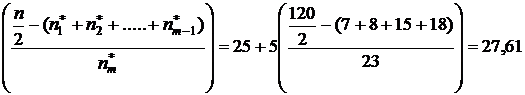 .
.
5. Для проверки гипотезы о нормальном распределении с помощью критерия согласия Пирсона составим расчетную таблицу 6, в которой Zi 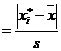 ; s=
; s= 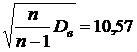 - исправленное выборочное среднее квадратическое отклонение.
- исправленное выборочное среднее квадратическое отклонение.
Рi= 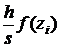 , для f(x)=
, для f(x)= 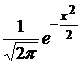 имеется таблица значений.
имеется таблица значений.
Таблица 6
| i | -βi | 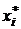
| 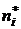
| zi | f(zi) | рi | npi | 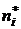 - npi - npi
| (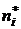 - npi)2 - npi)2
| (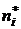 - npi) npi - npi) npi
|
| 5-10 | 7,5 | 1,8959 | 0,0656 | 0,0310 | 3,720 | 4,280 | 18,3184 | 4,924 | ||
| 10-15 | 12,5 | 1,4228 | 0,1456 | 0,0688 | 8,256 | 6,744 | 45,481 | 5,509 | ||
| 15-20 | 17,5 | 0,9498 | 0,2541 | 0,1202 | 14,424 | 0,576 | 0,332 | 0,023 | ||
| 20-25 | 22,5 | 0,4768 | 0,3555 | 0,1682 | 20,184 | -2,184 | 4,769 | 0,236 | ||
| 25-30 | 27,5 | 0,0037 | 0,3989 | 0,1887 | 22,644 | 0,356 | 0,127 | 0,006 | ||
| 30-35 | 32,5 | 0,4692 | 0,3572 | 0,1689 | 20,268 | -1,268 | 0,608 | 0,079 | ||
| 35-40 | 37,5 | 0,9422 | 0,2565 | 0,1213 | 14,556 | -0,556 | 0,309 | 0,021 | ||
| 40-45 | 42,5 | 1,4153 | 0,1456 | 0,0688 | 8,256 | 1,744 | 3,041 | 0,368 | ||
| 45-50 | 47,5 | 1,8883 | 0,0669 | 0,0316 | 3,792 | 2,208 | 4,875 | 1,286 | ||
| ∑ | 12,452 |
Наблюдаемое значение статистики Пирсона χ2набл.= 12,5.
Определяем критическую точку статистики Пирсона по таблице значений χ 2 при α= 1- γ= 1–95=0,05, к=т -3=9–6, χ 2кр.= χ 2 0,05(6)=12,6.
Сравним χ 2набл. и χ 2кр.: χ 2набл. < χ 2кр..
И в соответствии с разрешающим правилом критерия Пирсона гипотеза, нормальности согласуется с данной выборкой.
6. Доверительный интервал для оценки математического ожидания имеет вид: 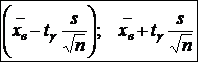 n= 120,
n= 120, 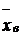 = 27,54, S=
= 27,54, S= 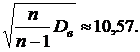
По таблице значений функции tγ=t(γ,n) при γ= 0,95 и n= 120 находим tγ= 1,98, доверительный интервал:
уγ= 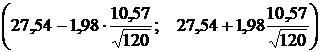 , уγ =(25,63; 29,45).
, уγ =(25,63; 29,45).
Доверительный интервал для оценки среднего квадратического отклонения имеет вид:
(s (1 -q); s (1 +q)) (при q< 1), s= 10,57. По таблице значений функции q=q(γ,n) при γ=0,95 и n= 120.
Находим q= 0,13<1.
уγ= (10,57(1-0,13); 10,57(1+0,13)),
уγ =(9,20; 11,94)
Литература
Основная литература
1. Гмурман В.Е. Теория вероятностей и математическая статистика [Текст] / В.Е. Гмурман. – М.: Высшая школа, 2009. – 479 с.
2. Ермолаев О.Ю. Математическая статистика для психологов [Текст]: Учебник для вузов / О.Ю. Ермолаев. – М.: МПСУ, 2011.– 336 с.
3. Письменный Д.Т. Конспект лекций по теории вероятностей, математической статистике и случайным процессам [Текст] / Д.Т. Письменный. - М.: Айрис-пресс, 2008. -288 с.
Дополнительная литература
1. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике [Текст] / В.Е. Гмурман. – М.: ОНИКС. Мир и Образование, 2004. – 405 с.
2. Чебыкин Л.С. Высшая математика: Элементы теории вероятностей и математической статистики: Курс лекций [Текст] / Л.С. Чебыкин. – Свердл. инж.-пед. ин-т. Свердловск, 1981. – 154 с.
ЗАДАНИЯ И МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ
КОНТРОЛЬНОЙ РАБОТЫ ПО ДИСЦИПЛИНЕ
«МАТЕМАТИЧЕСКАЯ СТАТИСТИКА»
Подписано в печать _________. Формат 60´84/16. Бумага для множ. аппаратов.
Печать плоская. Усл. печ. л. ___. Уч.-изд. л.____. Тираж ____ экз. Заказ № ____.
ФГАОУ ВПО «Российский государственный профессионально-педагогический университет». Екатеринбург, ул. Машиностроителей, 11.
Ризограф ФГАОУ ВПО РГППУ. Екатеринбург, ул. Машиностроителей, 11.
Date: 2015-07-22; view: 1751; Нарушение авторских прав