
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Случайные величины
|
|
Определение: Случайной величиной называется величина, которая в результате испытания принимает только одно из возможных значений, наперед неизвестное и зависящее от множества случайных причин, которые заранее не могут быть учтены.
Случайные величины обозначают заглавными буквами латинского алфавита X,Y,Z,…, а их возможные значения буквами x,y,z,…. Случайные величины подразделяются на дискретные и непрерывные.
Дискретная случайная величина принимает конечное или счетное множество значений, а всевозможные значения непрерывной случайной величины сплошь заполняют некоторый интервал.
Исчерпывающей характеристикой случайной величины является закон ее распределения. Законы распределения дискретной случайной величины: ряд распределения; функция распределения; многоугольник распределения. Законы распределения непрерывной случайной величины: функция распределения F(х), плотность распределения f (х).
Некоторые часто встречающиеся формулы:
F(х)= Р (Х <х) (9)
f (x) = F'(х) (10)
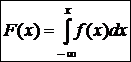 (11)
(11)
P(α <Х < β)=F(β)-F(α) (12)
Р(α<х<β)= 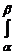 f (x)dx, (13)
f (x)dx, (13)
Числовые характеристики случайной величины позволяют выразить в сжатой форме существенные особенности распределения случайной величины.
Для дискретной случайной величины (случай конечного множества значений) математическое ожидание определяется по формуле:
М(х)=х1 р1 +х2 р2 + ……+х n pn, (14)
дисперсия (рабочая формула)
D(x)=M(x2)- 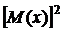 (15)
(15)
среднее квадратическое отклонение
σ(Х) = 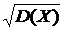 . (16)
. (16)
Для непрерывной случайной величины: математическое ожидание
М(Х)= 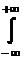 хf(x)dx (17)
хf(x)dx (17)
дисперсия (рабочая формула)
D(X)= 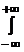 x2f(x)dx- x2f(x)dx- 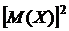
| (18) |
cреднее квадратическое отклонение
σ(Х)= 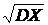 . (19)
. (19)
Задача 8. Монета брошена три раза. Составить ряд распределения вероятностей случайной величены Х – числа выпадений герба. Построить многоугольник распределения случайной величины Х, найти функцию распределения F(X) и построить ее график. Найти математическое ожидание М(Х), дисперсию D(X), среднее квадратическое отклонение σ(Х).
Решение: Вероятность появления герба в каждом испытании (бросании монеты) равна р= 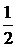 , следовательно, вероятность непоявления герба q можно определить по формуле q= 1– р, то есть q= 1 –
, следовательно, вероятность непоявления герба q можно определить по формуле q= 1– р, то есть q= 1 – 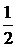 =
= 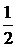 . При трех бросаниях монеты герб может совсем не появиться, либо появиться один раз, два, либо три раза. Таким образом, возможные значения величины Х: х0= 0; х1= 1; х2= 2; х3 =3.
. При трех бросаниях монеты герб может совсем не появиться, либо появиться один раз, два, либо три раза. Таким образом, возможные значения величины Х: х0= 0; х1= 1; х2= 2; х3 =3.
Найдем вероятности этих возможных значений по формуле Бернулли (10) при т= 0,1,2,3.
Р(Х= 0 )=Р3( 0 )=С03 р0q3=(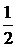 )3=
)3= 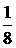 ;
;
Р(Х= 1 )=Р3( 1 )=С13 р1q2 = 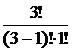 (
(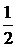 )1(
)1(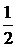 )2=
)2= 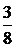 ;
;
Р(Х= 2 )=Р3(2)=С23 р2q1 = 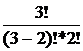 (
(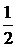 )2
)2 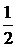 =
= 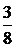 ;
;
Р(Х= 3 )=Р3( 3 )=С33 р3q0 = (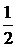 )3=
)3= 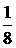 ;
;
Запишем искомый закон биноминального распределения в виде распределения (таблица 1).
 Таблица 1
Таблица 1
| xi | ||||
| pi | 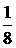
| 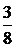
| 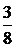
| 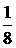
|
Рис.1. Многоугольник распределения
В целях контроля вычислений сложим вероятности всех возможных значений 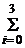 pi=
pi= 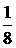 +
+ 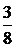 +
+ 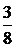 +
+ 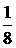 = 1(что и следовало ожидать).
= 1(что и следовало ожидать).
Построим многоугольник распределения (рис.1).
Составим функцию распределения F(X):
1. 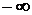 < х ≤0, F(x)= 0,
< х ≤0, F(x)= 0,
2. 0< x ≤1, F(x)=  P(X=xi)=P(X= 0 )=
P(X=xi)=P(X= 0 )= 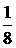 ,
,
3. 1< x ≤2, F(x)=  P(X=xi)=
P(X=xi)= 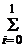 Pi=
Pi= 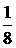 +
+ 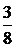 =
= 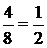 ,
,
4. 2< x ≤3, F(x)=  P(X=xi)=
P(X=xi)= 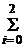 Pi=
Pi= 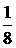 +
+ 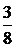 +
+ 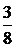 =
= 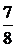 ,
,
5. 3< x≤ +∞, F(x)=  P(X=xi)=
P(X=xi)= 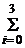 Pi=
Pi= 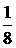 +
+ 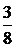 +
+ 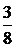 +
+ 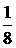 =1.
=1.
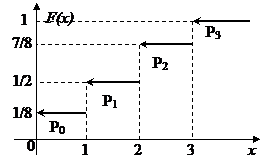 Или:
Или:
0 при -∞ <x≤ 0;
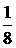 при 0 <x≤ 1;
при 0 <x≤ 1;
F(x)= 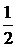 при 1 <x≤ 2;
при 1 <x≤ 2;
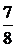 при 2 <x≤ 3;
при 2 <x≤ 3;
1 при 3 <x≤ +∞.
Рис. 2. График функции распределения
Составленную функцию распределения изобразим графически (рис. 2).
Найдем математическое ожидание М(Х):
М(Х)= 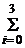 xi pi= 0
xi pi= 0 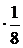 +1
+1 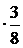 +2
+2 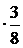 +3
+3 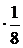 =
= 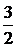 .
.
Найдем математическое ожидание М(Х2):
М(Х2)= 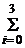 xi2 pi =02
xi2 pi =02 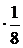 +12
+12 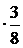 +22
+22 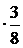 +32
+32 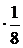 =3.
=3.
Найдем дисперсию Д(Х)=М(Х2) – 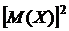 = 3 – (
= 3 – (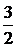 )2=
)2= 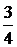 ,
,
Среднее квадратическое отклонение равно: σ(х)= 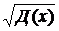 =
= 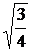 =
= 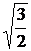 ≈ 0,87.
≈ 0,87.
Задача 9. Случайная величина Х задана функцией распределения.
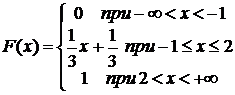
Найти: а) вероятность того, что в результате испытания случайная величина Х окажется в пределах промежутка (0;1); б) плотность распределения вероятностей f(x), построить графики F(x), f(x); в) математическое ожидание М(Х), дисперсию Д(Х) и среднее квадратическое отклонение σ(Х).
Решение: а) Пользуясь формулой Р(α<X<β)=F(β)-F(α), найдем Р(0<X<1)= F(1)–F(0)= 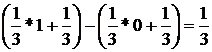 .
.
б) По формуле f(x) = F'(x) находим:
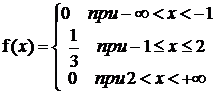 .
.
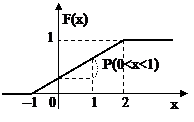 | 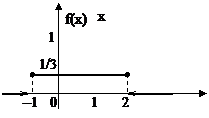 | ||
Рис.3. График функции F(x) Рис.4. График функции f(x)
в) Найдем математическое ожидание по формуле: М(Х)= 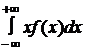 .
.
М(Х)= 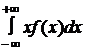 =
= 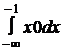 +
+ 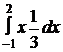 +
+ 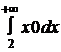 =
= 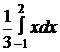 =
= 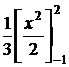 =
= 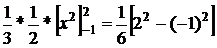 =
= 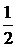 .
.
Для вычисления дисперсии Д(Х) воспользуемся формулой Д(Х)= М(Х2)- 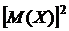 . Вычислим М(Х2):
. Вычислим М(Х2):
М(Х2)= 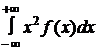 =
= 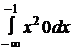 +
+ 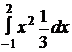 +
+ 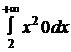 =
= 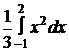 =
= 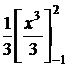 =
=
= 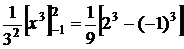 =1.
=1.
Д(Х)= М(Х2)– 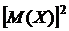 =1-
=1- 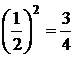 .
.
Среднее квадратическое отклонение σ(Х) вычисляем по формуле:
σ(Х)=  , σ(Х)=
, σ(Х)= 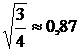 .
.
Date: 2015-07-22; view: 943; Нарушение авторских прав