
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Задача 5
|
|
Методические указания для выполнения контрольной работы
При выполнении контрольной работы необходимо соблюдать следующие требования:
1. Вариант контрольной работы выбирать по последней цифре номера зачетной книжки.
2. Каждую контрольную работу следует выполнять в отдельной тонкой тетради.
3. На обложке тетради должны быть ясно написаны название дисциплины; номер контрольной работы; фамилия, имя, отчество студента; шифр специальности и номер группы; номер зачетной книжки.
4. В начале работы должен быть указан номер варианта.
5. Перед выполнением каждого задания следует полностью привести его условие.
6. Выполнение заданий контрольной работы следует сопровождать краткими пояснениями.
7. В конце работы должна стоять личная подпись студента и дата выполнения контрольной работы.
Содержание контрольной работы
Задача 1.
1.1. Абонент забыл последнюю цифру номера телефона и потому набирает ее на удачу. Определить вероятность того, что ему придется звонить не более чем в три места.
1.2. Студент знает 45 из 60 вопросов программы. Каждый экзаменационный билет содержит три вопроса. Найти вероятность того, что: а) студент знает все три вопроса, содержащиеся в его экзаменационном билете; б) студент знает только два вопроса своего экзаменационного билета; в) студент знает только один вопрос своего экзаменационного билета.
1.3. Вероятность улучшения спортсменом личного достижения по прыжкам в длину равна 0,4. Чему равна вероятность того, что он улучшит свой результат, если ему предоставлена возможность прыгать три раза.
1.4. Рабочий обслуживает три станка, на которых обрабатываются однотипные детали. Вероятность брака для первого станка равна 0,02, для второго – 0,03, для третьего – 0,04. Обработанные детали складывают в один ящик. Производительность первого станка в три раза больше, чем второго, а третьего в 2 раза меньше, чем второго. Определить вероятность того, что взятая из ящика наудачу деталь будет бракованной.
1.5. В урне 10 белых и 5 черных шаров. Чему равна вероятность того, что, вынув наудачу с возвращением 6 шаров, получим белых не менее 3-х.
1.6. На факультете насчитывается 1460 студентов. Какова вероятность того, что 1 сентября является днем рождения одновременно пяти студентов.
1.7. Три стрелка в одинаковых независимых условиях произвели по одному выстрелу по одной и той же мишени. Вероятность поражения мишени первым стрелком равна 0,9, вторым – 0,8, третьим – 0,7. Найти вероятность того, что: а) только один из стрелков попадет в мишень; б) только два стрелка попадут в мишень; в) все три стрелка попадут в мишень.
1.8. В первой бригаде токарей 2 рабочих имеют первый разряд, 2 рабочих – второй, 5 рабочих – четвертый. Во второй бригаде 1 токарь имеет первый разряд, 4 токаря – третий, 2 токаря – четвертый. Из первой бригады во вторую переведен один токарь. Найти вероятность того, что рабочий, наудачу выбранный из нового состава второй бригады, имеет разряд не ниже второго.
1.9. В правом кармане имеется три монеты по 1 рублю и четыре монеты по 50 копеек, а в левом - шесть монет по 1 рублю и три монеты по 50 копеек. Из правого кармана в левый наудачу перекладываются пять монет. Определить вероятность извлечения из левого кармана (после перекладывания) монеты в 1 рубль, если монета берется наудачу.
1.10. Вероятность нарушения работы кинескопа телевизора в течение гарантийного срока равна 0,12. Найти вероятность того, что из 46 наблюдаемых телевизоров более 36 выдержат гарантийный срок.
Задача 2.
Дискретная случайная величина 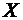 может принимать только два значения
может принимать только два значения 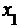 и
и 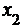 , причем
, причем 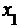 <
< 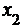 . Известны вероятность
. Известны вероятность 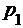 возможного значения
возможного значения 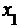 , математическое ожидание
, математическое ожидание 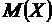 и дисперсия
и дисперсия 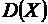 . Найти закон распределения этой случайной величины:
. Найти закон распределения этой случайной величины:
2.1. 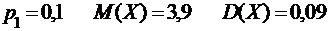
2.2. 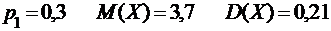
2.3. 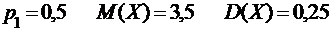
2.4. 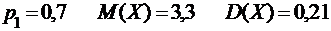
2.5. 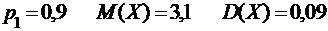
2.6. 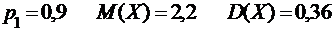
2.7. 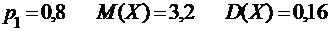
2.8. 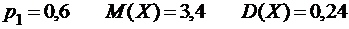
2.9. 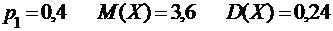
2.10. 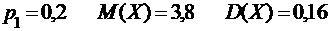
Задача 3.
Случайная величина 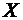 задана функцией распределения (интегральной функцией)
задана функцией распределения (интегральной функцией) 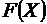 . Найти плотность распределения вероятностей (дифференциальную функцию)
. Найти плотность распределения вероятностей (дифференциальную функцию) 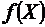 , математическое ожидание
, математическое ожидание 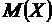 и дисперсию
и дисперсию 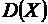 . Построить графики интегральной и дифференциальной функций:
. Построить графики интегральной и дифференциальной функций:
3.1. 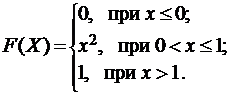 3.2.
3.2. 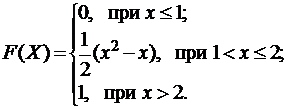
3.3. 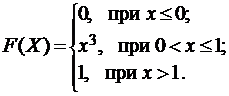 3.4.
3.4. 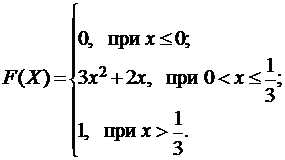
3.5. 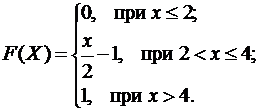 3.6.
3.6. 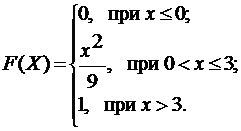
3.7. 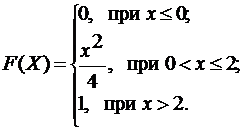 3.8.
3.8. 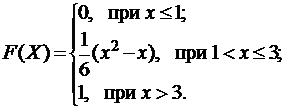
3.9. 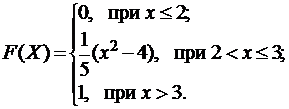
3.10. 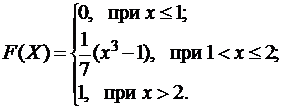
Задача 4.
Известны математическое ожидание 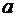 и среднее квадратическое отклонение
и среднее квадратическое отклонение 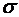 нормально распределенной случайной величины
нормально распределенной случайной величины 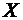 . Найти вероятность попадания этой случайной величины в заданный интервал
. Найти вероятность попадания этой случайной величины в заданный интервал 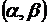 .
.
4.1.  .
.
4.2. 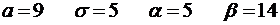 .
.
4.3. 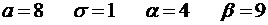 .
.
4.4. 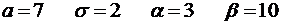 .
.
4.5. 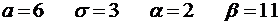 .
.
4.6. 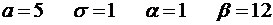 .
.
4.7. 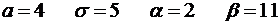 .
.
4.8. 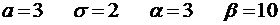 .
.
4.9.  .
.
4.10. 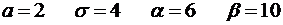 .
.
Задача 5.
Из генеральной совокупности 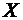 , распределенной по нормальному закону, извлечена выборка. Требуется:
, распределенной по нормальному закону, извлечена выборка. Требуется:
1. Составить вариационный, статистический и выборочный ряды распределения; найти размах выборки;
По полученному распределению выборки:
2. Построить полигон относительных частот;
3. Построить график эмпирической функции распределения;
4. Вычислить выборочную среднюю, выборочную дисперсию, выборочное исправленное среднее квадратическое отклонение, моду и медиану;
5. С надежностью 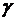 найти доверительные интервалы для оценки математического ожидания и среднего квадратического отклонения изучаемого признака генеральной совокупности.
найти доверительные интервалы для оценки математического ожидания и среднего квадратического отклонения изучаемого признака генеральной совокупности.
5.1. 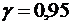
| 5,0 | 5,6 | 5,8 | 5,4 | 5,8 | 5,2 | 5,0 | 5,6 |
| 5,6 | 5,6 | 5,4 | 5,2 | 5,4 | 5,8 | 5,4 | 5,6 |
| 5,4 | 5,4 | 5,4 | 5,2 | 5,6 | 6,0 | 5,0 | 5,8 |
| 5,2 | 5,8 | 5,6 | 5,2 | 6,0 | 5,8 | 6,0 | 5,8 |
| 5,4 | 6,2 | 5,6 | 6,2 | 5,6 | 5,6 | 6,0 | 5,2 |
5.2. 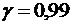
5.3. 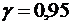
| 7,6 | 7,8 | 7,4 | 7,8 | 7,2 | 7,6 | ||
| 7,6 | 7,6 | 7,4 | 7,2 | 7,4 | 7,8 | 7,4 | 7,6 |
| 7,4 | 7,4 | 7,4 | 7,2 | 7,6 | 7,8 | ||
| 7,2 | 7,8 | 7,6 | 7,2 | 7,8 | 7,8 | ||
| 7,4 | 8,2 | 7,6 | 8,2 | 7,6 | 7,6 | 7,2 |
5.4. 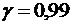
| 13,1 | 11,1 | 12,1 | 9,1 | 12,2 | 12,1 | 10,1 | 12,1 |
| 15,1 | 11,1 | 13,1 | 14,1 | 13,1 | 11,1 | 11,1 | 12,1 |
| 13,1 | 11,1 | 12,1 | 11,1 | 10,1 | 14,1 | 12,1 | 10,1 |
| 9,1 | 10,1 | 12,1 | 15,1 | 9,1 | 13,1 | 11,1 | 13,1 |
| 12,1 | 12,1 | 14,1 | 11,1 | 10,1 | 14,1 | 12,2 | 12,1 |
5.5. 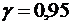
| 11,7 | 12,3 | 11,1 | 10,8 | 11,4 | 11,1 | 11,1 | 11,4 |
| 11,4 | 11,4 | 11,7 | 11,1 | 12,3 | 11,1 | 10,5 | |
| 10,8 | 10,5 | 10,8 | 11,1 | 11,7 | 11,7 | ||
| 11,4 | 11,1 | 11,4 | 11,4 | 11,4 | 10,8 | 11,4 | |
| 10,5 | 11,7 | 11,4 | 11,4 | 11,7 | 11,4 | 11,4 | 10,8 |
5.6. 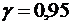
| 11,6 | 11,8 | 11,4 | 11,8 | 11,2 | 11,6 | ||
| 11,6 | 11,6 | 11,4 | 11,2 | 11,4 | 11,8 | 11,4 | 11,6 |
| 11,4 | 11,4 | 11,4 | 11,2 | 11,6 | 11,8 | ||
| 11,2 | 11,8 | 11,6 | 11,2 | 11,8 | 11,8 | ||
| 11,4 | 12,2 | 11,6 | 12,2 | 11,6 | 11,6 | 11,2 |
5.7. 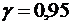
| 12,5 | 10,5 | 11,5 | 8,5 | 11,5 | 11,5 | 9,5 | 11,5 |
| 14,5 | 10,5 | 12,5 | 13,5 | 12,5 | 10,5 | 10,5 | 11,5 |
| 12,5 | 10,5 | 11,5 | 10,5 | 9,5 | 13,5 | 11,5 | 9,5 |
| 8,5 | 9,5 | 11,5 | 14,5 | 8,5 | 12,5 | 10,5 | 12,5 |
| 11,5 | 11,5 | 13,5 | 10,5 | 9,5 | 13,5 | 11,5 | 11,5 |
5.8. 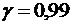
| 12,7 | 13,3 | 12,1 | 11,8 | 12,4 | 12,1 | 12,1 | 12,4 |
| 12,4 | 12,4 | 12,7 | 12,1 | 13,3 | 12,1 | 11,5 | |
| 11,8 | 11,5 | 11,8 | 12,1 | 12,7 | 12,7 | ||
| 12,4 | 12,1 | 12,4 | 12,4 | 12,4 | 11,8 | 12,4 | |
| 11,5 | 12,7 | 12,4 | 12,4 | 12,7 | 12,4 | 12,4 | 11,8 |
5.9. 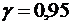
| 13,6 | 13,8 | 13,4 | 13,8 | 13,2 | 13,6 | ||
| 13,6 | 13,6 | 13,4 | 13,2 | 13,4 | 13,8 | 13,4 | 13,6 |
| 13,4 | 13,4 | 13,4 | 13,2 | 13,6 | 13,8 | ||
| 13,2 | 13,8 | 13,6 | 13,2 | 13,8 | 13,8 | ||
| 13,4 | 14,2 | 13,6 | 14,2 | 13,6 | 13,6 | 13,2 |
5.10. 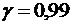
Date: 2015-07-22; view: 1644; Нарушение авторских прав