Комплексные числа. Выражение вида , где и - вещественные числа, , называется комплексным числом (в алгебраической форме)

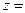
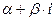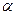Выражение вида , где и 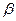- вещественные числа, , называется комплексным числом (в алгебраической форме).

Комплексное число 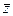= 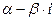называется комплексно-сопряженным числом к комплексному числу .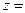

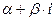Действия над комплексными числами. Пусть даны два комплексных числа: 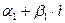и 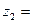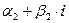. Тогда

1)

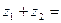
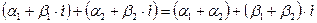
2)

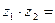
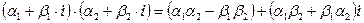
3) = .

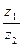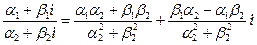Для любого комплексного числа 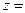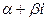имеем: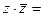

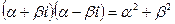
Величина 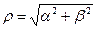называется модулем комплексного числа. Угол 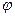, определяемый равенствами 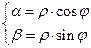, , 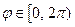называется аргументом комплексного числа.

Любое комплексное число можно записать в тригонометрической форме:

,

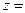
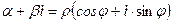где .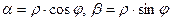

Для выполнения действий возведения комплексного числа в натуральную степень и извлечения корня с натуральным показателем используются формулы Муавра:

1) ;

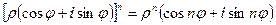2) , .

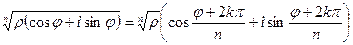Задание 5 Дано комплексное число 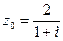. Требуется:

1) записать данное число в алгебраической и тригонометрической формах;

2) найти все корни уравнения .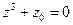

Решение 1) Приведем комплексное число к алгебраической форме: .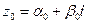

Для этого умножим числитель и знаменатель дроби на число 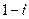, комплексно-сопряженное знаменателю. Получим:

.

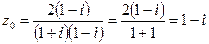Это и есть алгебраическая формакомплексногочисла , где .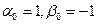

Теперь приведем комплексное число 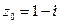к тригонометрическому виду: 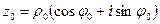, где - модуль комплексного числа , - аргумент этого числа.

Для этого найдем 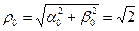. Для нахождения имеем систему:

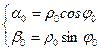
или

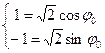
и тогда 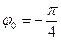. Следовательно, тригонометрическая форма комплексного числа 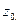имеет вид:

.

3) Найдем теперь все корни уравнения 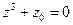, откуда 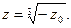Тригонометрическая форма комплексного числа - имеет вид: .

По второй из формул Муавра получаем:

, где

Тогда корни уравнения имеют вид:

1. При ;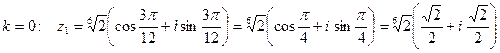

2. При ;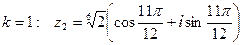

3. При .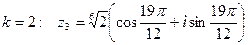

Date: 2015-07-11; view: 368; Нарушение авторских прав