Метод Гаусса решения произвольных систем линейных алгебраических уравнений

Рассмотрим систему m линейных алгебраических уравнений с n неизвестными:

. (3)

Матрица

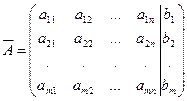(4)

называется расширенной матрицей системы (3).

Элементарными преобразованиями матрицы 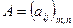называются следующие действия:

1) перестановка строк (столбцов);

2) умножение строки (столбца) на число, отличное от нуля;

3) прибавление к элементам строки (столбца) соответствующих элементов другой строки (столбца), предварительно умноженных на некоторое число.

С помощью элементарных преобразований любая матрица может быть

приведена к трапециевидному виду.

Метод Гаусса заключается в приведении расширенной матрицы системы к трапециевидному виду с помощью элементарных преобразований, выполняемых над строками матрицы. Таким образом, расширенная матрица (4) может быть приведена к виду:

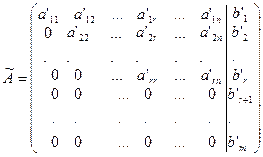, (5)

где .

Матрица (5) является расширенной матрицей системы

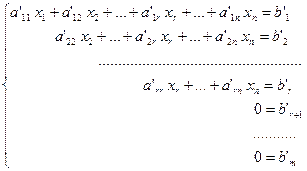. (6)

Система (6) эквивалентна исходной системе (3).

Если хотя бы одно из чисел 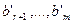отлично от нуля, то система (6), а, следовательно, и исходная система (3) не совместна, то есть не имеет решений.

Если же 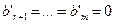, то система (6) совместна. Следовательно, совместна и исходная система (3).

Задание 4. Найти решение системы методом Гаусса:

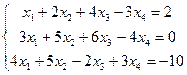. (7)

Решение.

Расширенная матрица системы (7) имеет вид:

Приведем эту матрицу к трапециевидному виду с помощью элементарных преобразований. Для этого умножим элементы первой строки матрицы на (-3) и сложим с соответствующими элементами второй строки. Затем умножим элементы первой строки матрицы на (-4) и сложим с соответствующими элементами третьей строки. В результате получим:

.

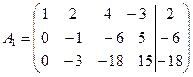Теперь умножим элементы второй строки матрицы 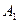на (-3) и сложим с соответствующими элементами третьей строки. Получим:

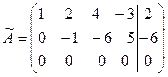. (8)

Матрица 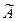является расширенной матрицей системы

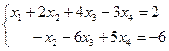. (9)

Система (9) эквивалентна исходной системе (7). Система (9) содержит два уравнения с 4-мя неизвестными, следовательно, две неизвестные могут быть выбраны произвольно. Придавая неизвестным и 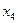произвольные значения 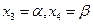, получаем решение системы (7) в виде

где α, β - любые числа.

Date: 2015-07-11; view: 316; Нарушение авторских прав