Аналитическая геометрия на плоскости

Общее уравнение прямой на плоскости имеет вид

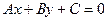, где .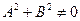

Вектор , перпендикулярный прямой, называется нормальным вектором прямой на плоскости.

Уравнение вида , где 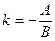, , 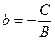, 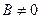называется уравнением прямой с угловым коэффициентом.

Уравнение прямой, проходящей через данную точку с заданным угловым коэффициентом, имеет вид:

.

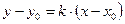Угол между прямыми , 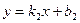определяется следующим образом:

.

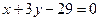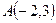Задание 2. Даны уравнения двух высот треугольника и , и одна из вершин . Составить уравнения сторон треугольника. Сделать чертеж.

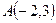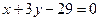Решение. По условию задачи нам известны: , CD: и BE: 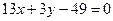. Определим уравнение стороны AB. Высота CD перпендикулярна стороне AB, а потому их угловые коэффициенты 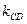и 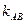удовлетворяют условию: 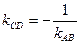. Из уравнения прямой CD следует, что . Тогда .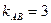

Напишем уравнение прямой, проходящей через данную точку с заданным угловым коэффициентом:

.

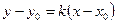Подставив в это уравнение координаты точки А и угловой коэффициент 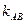,получим уравнение стороны АВ:

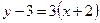
или

.

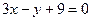Аналогично можно получить и уравнение стороны АС. Действительно, в силу перпендикулярности ВЕ и АС имеем: 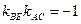. Из уравнения высоты ВЕ следует, что . Тогда 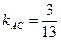. Следовательно, подставив в уравнение прямой, проходящей через данную точку с заданным угловым коэффициентом, координаты точки А и угловой коэффициент 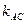, получим уравнение стороны АС:

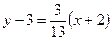
или

.

Теперь составим уравнение стороны ВС. Для этого определим координаты вершин В и С треугольника АВС. Координаты точки В можно определить из условия пересечения прямых АВ и ВЕ:

.

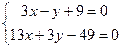Решение полученной системы и есть координаты вершины 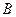, а именно .

Таким же образом определяем координаты точки С:

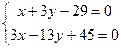
и тогда С .

Уравнение прямой, проходящей через точки В и С, имеет вид:

,

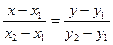где B 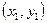, C .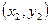

Подставив координаты точек В и С в данное уравнение, получим уравнение стороны ВС:

или

.

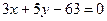Сделаем теперь чертеж:

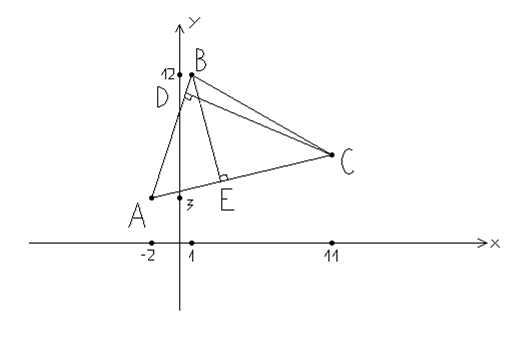
Date: 2015-07-11; view: 465; Нарушение авторских прав