Матрицы и действия над ними

Введение

При изучении курса высшей математики студент-заочник должен выполнить ряд контрольных работ. Решения задач и пояснения к ним должны быть достаточно подробными. Все решения надо приводить полностью, чертежи и графики должны быть выполнены четко, с указанием масштаба и названий координатных осей. Обозначения к задачам должны соответствовать указаниям на чертежах и графиках. К выполнению контрольного задания следует приступать после изучения теоретического материала по учебникам и решения достаточного количества задач по материалу, соответствующему этому заданию.

Настоящее пособие является руководством по выполнению контрольных работ по курсу высшей математики для студентов-заочников экономических специальностей вузов. Оно содержит вопросы и теоретические сведения, необходимые для выполнения контрольных работ по данной теме, примеры решения задач, контрольные задания и список литературы.

Глава I. Основы линейной алгебры

Теоретические вопросы

1. Матрицы и действия над ними.

2. Определители второго и третьего порядков, их свойства. Миноры и

алгебраические дополнения.

3. Обратная матрица.

4. Системы линейных алгебраических уравнений. Теорема Крамера. Матричный способ решения алгебраических уравнений. Метод Гаусса.

5. Собственные значения и собственные векторы матрицы.

Литература

В.А. Кудрявцев, Б.П. Демидович. Краткий курс высшей математики. -М.: Наука, 1978.

1. В.А. Ильин, Э.Г. Позняк. Линейная алгебра. - М.: Наука, 1978.

2. П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. Высшая математика в упражнениях и задачах. - М.: Высшая школа, 1998, ч.1,2.

Матрицы и действия над ними

Таблица чисел, содержащая m строк и n столбцов вида

,

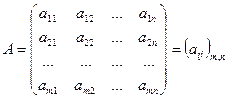называется матрицей порядка 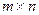. Матрица порядка 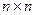называется квадратной матрицей порядка п (А = ).

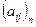Две матрицы 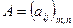и 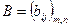называются равными (А=В), если равны их соответствующие элементы, т.е. 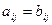(i =1,…,m; j =1,…,n).

Суммой двух матриц 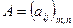и 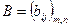одинакового порядка называется матрица 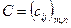(С = A+B), элементы которой определяются равенствами

(i =1,…,m; j =1,…,n).

Произведением матрицы 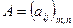на число 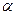называется матрица 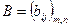(В = 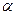А или B = А 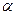), элементы которой определяются равенствами

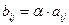(i =1,…,m; j =1,…,n).

Произведением матрицы 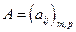на матрицу 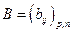называется матрица 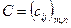(С = AB), элементы которой определяются равенствами

.

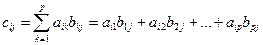
Заметим, что умножение матрицы А на матрицу В определяется только при условии, что число столбцов матрицы А равно числу строк матрицы В.

Задание 1. Выполнить действия над матрицами А и В:(2A-B)(A+3B), где

.

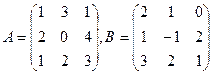Решение. Данное выражение содержит следующие операции над матрицами:

1) произведение матрицы на число.

2) сумма двух матриц;

3) произведение двух матриц.

Используя определения, данные выше, получим:

;

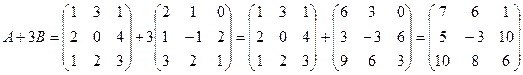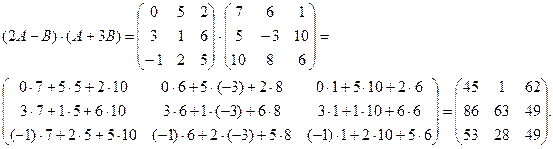
Date: 2015-07-11; view: 549; Нарушение авторских прав