II Учет граничных условий. Коэффициент отражения

Решив уравнения для тока и напряжения, мы должны найти const интегрирования A, B, пользуясь граничными условиями. Рассмотрим рисунок 97.

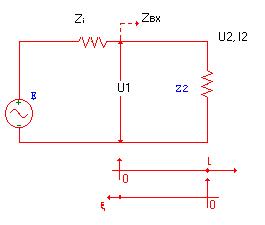Рис.97

Граничные условия имеют вид:

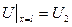
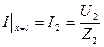. Применяя эти уравнения к уравнениям (171), (173) будем иметь: 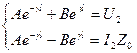Отсюда находим A, B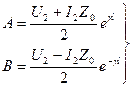

Теперь выражения для токов и напряжений примут вид:

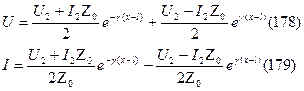
Первые слагаемые - прямая волна / падающая волна /.

Вторые слагаемые - обратная волна / отраженная волна /.

Коэффициент отражения равен:

(180) - для напряжения.

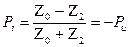(181) - для тока.

Если линия нагружена на произвольное комплексное сопротивление, то и коэффициент отражения будет комплексным:

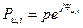, где p- модуль, 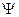- сдвиг фаз (= ).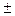

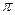Преобразуем (178) и (179) подстановкой 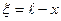тогда получим:

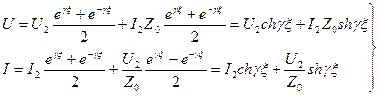(182)

Входное сопротивление лини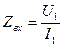и (при ) равно:

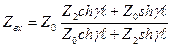(183)

Для того, чтобы выразить 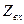через коэффициент отражения, перепишем уравнения (178) и (179) через коэффициент отражения при x=0 с учетом (180)

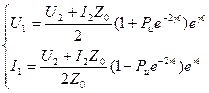
Отсюда 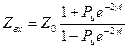(184)