
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Тема 6. Межотраслевой баланс производства и распределения продукции
|
|
Любое современное национальное хозяйство развивается в сложной системе межотраслевых взаимосвязей, понять которые во всей совокупности путем простых рассуждений невозможно.
Например, спрос на автомобили оказывает влияние не только на автомобильную промышленность, но косвенно влияет на металлургическую, на отрасли, связанные с производством комплектующих деталей и т.д.
Метод межотраслевого анализа, или :анализа затрат -выпуск, разработанный американским экономистом В.В. Леонтьевым,. родившимся в России, позволяет численно определить взаимное влияние отраслей на их макроэкономические показатели.
Межотраслевой анализ основывается на использовании таблиц, дающих картину народнохозяйственной динамики за определенный период (например, за один год), содержание которых составляют связи между отраслями (табл. 1).
По экономическому содержанию и характеру информации выделяют следующие их разновидности балансов: стоимостные, натуральные и натурально-стоимостные, каждый из них, в свою очередь, может быть отчетным и плановым. Наряду с балансами, охватывающими все национальное хозяйство, разрабатываются: региональные межотраслевые балансы, балансы экономических районов. Принципы межотраслевого баланса используются для построения внутриотраслевых межпродуктовых балансов, характеризующих связи между суботраслями и видами производства внутри крупных отраслей национального хозяйства.
Стоимостные межотраслевые балансы характеризуют процессы воспроизводства в денежном выражении. Балансы этого типа охватывают все четыре квадранта принципиальной схемы. По своей структуре стоимостные балансы могут быть укрупненными и детальными.
Таблица 1
| Отрасли производители | Отрасли потребители | |||||||||
| Совокупный общественный продукт | ||||||||||
| Промежуточный продукт | Конечный продукт | |||||||||
| Национальный доход | ||||||||||
| Металлургия | Электроэнергетика | Возмещение выбытия и кап.рем.осн. фондов | Фонд потребления | Фонд накопления | Экспорт Импорт | Итого | Всего | |||
| Текущие материальные затраты | ||||||||||
| 1.Металлургия 2.Энергетика I квадрант II квадрант | ||||||||||
| Стоимость конечногопродукта | Амортизация Доходы трудящихся Чистый доход предприятий Централизованный чистый доход III квадрант IV квадрант государства Итого | |||||||||
| Всего | ||||||||||
Межотраслевой баланс в натуральном выражении разрабатывается по важнейшим видам продукции. Его номенклатура включает несколько сот наименований продукции и не охватывает всего общественного производства. Схема межотраслевого баланса в натуральном выражении содержит показатели только I и II квадрантов принципиальной схемы межотраслевого баланса. Натурально-стоимостной межотраслевой баланс включает все отрасли национального хозяйства, а также важнейшие виды продукции в натуральном и стоимостном выражении.
Отчетные межотраслевые балансы фиксируют межотраслевые потоки продукции, их направление и, формы использования конечного продукта по назначению, а также процесс создания и использования национального дохода. В качестве исходной информации могут использоваться данные текущей статистики и специального обследования.
При построении статистической открытой модели межотраслевого баланса используется следующая система предпосылок.
1-я предпосылка
Все хозяйство (район и т.д.) можно разбить на n отраслей (или n продуктов). Реализация этой предпосылки на практике требует серьезной содержательной работы
2-я предпосылка
В каждой отрасли производится только один продукт и одним способом. Иными словами, не существует других вариантов, кроме фиксированного варианта получения продукции. Эта предпосылка, существенная с точки зрения балансовой модели, снимается в оптимальных моделях.
3-я предпосылка
Всю продукцию национального хозяйства можно разделить на промежуточную и конечную. Промежуточной называют ту часть продукции, которая идет в дальнейшую переработку в отрасли и образует текущие материальные затраты. Конечной называют, ту продукцию, которая окончательно покидает пределы годового производства и используется для потребления, накопления, экспорта. Так, например, ткань, идущая на продажу, является конечной продукцией. Сахар для переработки - промежуточный продукт, а сахар, реализуемый в торговой сети -конечный продукт.:
С учетом сделанных предпосылок отобразим математически межотраслевые связи. Для дальнейшего требуется, чтобы студенты повторили основы матричной алгебры: сложение и вычитание матриц, умножение матрицы на матрицу и матрицы на вектор, нахождение обратных матриц.
Пусть Хi - интенсивность валового выпуска i-й отрасли; Yi; - интенсивность конечной продукции i-й отрасли; xij интенсивность межотраслевого потока из i-й отрасли на воспроизводство валовой продукции j-й отрасли,
i,j=1,2,….,n
Тогда межотраслевые связи можно отобразить системой уравнений (баланс распределения продукции):
 |
X1=x11+x12+ + x1j+ + x1n+Y1
X2=x21+x22+ + x2j+ + x1n+Y1
Xi=xi1+ xi2+ + xij+ + xin+Yi (5.1)
X1=x11+ x12+ + xij+ + xnn+Yn
Однако построенная балансовая модель распределения валовой продукции дает бесчисленное множество сбалансированных,решений так как ее математический аналог - система из п уравнений с 2n+n2 неизвестными. Рассматриваемая модель нуждается в доопределении,
Предполагают, что межотраслевая поставка xij продукции i-й отрасли в j-ю отрасль зависит линейно от объема. валовой продукции потребителя Хj и от нормы материалоемкости аij, определяющей затраты продукции i-й отрасли на воспроизводство единицы валовой продукции j-й отрасли, т.е.
xij= аijXj, i,j=1,2,…,n (5.2)
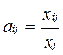
где 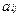 норма материалоемкости.
норма материалоемкости.
Тогда система уравнений (1) в предположении (2) примет вид
 X1=а11+а12+ + а1j+ + а1n+Y1
X1=а11+а12+ + а1j+ + а1n+Y1
X2=а21+а22+ + а2j+ + а1n+Y1
Xi=аi1+ аi2+ + аij+ + аin+Yi (5.3)
Xn=а11+ а12+ + аij+ + аnn+Yn
Или
Xj= 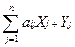 , j=1,2,….n (5.3’)
, j=1,2,….n (5.3’)
Экономико-математическую модель межотраслевого баланса распределения продукции можно представить также в матричной форме:
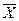 =
= 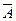 +
+ 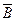 , (5.3”).,
, (5.3”).,
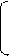 |  | ||
Х1
где 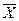 = Х2 -вектор интенсивности валового продукта;
= Х2 -вектор интенсивности валового продукта;
Х3
 | |||
 | |||
Y1
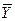 = Y2 -вектор интенсивности конечного продукта;
= Y2 -вектор интенсивности конечного продукта;
Y3
 |
а11а12 а1j а1n
а21 а22 а2j а1n
А= аi1 аi2 аij аin
а11 а12 аij аnn
матрица материалоемкости (матрица коэффициентов прямых затрат).
Система уравнений (5.3), или (5.3'),(5.З") в отличие от системы уравнений (5.1) содержит неизвестных n компонент валовой 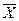 и n компонент конечного продукта
и n компонент конечного продукта 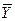 . Для получения единственного решения n переменных задают экзогенно. Так, в задаче управляемости фиксируют конечный продукт
. Для получения единственного решения n переменных задают экзогенно. Так, в задаче управляемости фиксируют конечный продукт 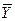 и по нему определяют валовой продукт
и по нему определяют валовой продукт 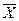 .
.
В задачах наблюдаемости процесса распределения валового продукта входом в модель (экзогенным фактором) является валовой продукт 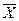 , а выходом является конечный продукт Y. В модели наблюдаемости систему балансовых соотношений разрешают относительно вектора конечного продукта, что в матричной форме имеет вид:
, а выходом является конечный продукт Y. В модели наблюдаемости систему балансовых соотношений разрешают относительно вектора конечного продукта, что в матричной форме имеет вид:
(Е-А) 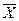 =
= 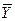
где Е - единичная матрица, элементы главной диагонали которой есть единицы, а остальные элементы матрицы - нули.
Кибернетически модель распределения валовой продукции можно представить в виде (рис. 1).
|
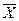
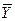


Рис.1
где (E - А) - оператор идентификации (матричный оператор преобразования вектора валового продукта 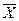 в вектор конечного продукта
в вектор конечного продукта 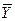
В задаче планирования система уравнений связи разрешается относительно вектоpa валовой продукции:
(Е-А) 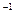
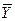 =
= 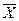 (5.5)
(5.5)
Кибернетическим аналогам управлени является преобразователь вектора конечного продукта в вектор валового продукта (рис.2).
|
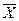
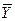


Рис.2
где (Е-А) 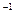 •- оператор управления, преобразующий экзогенный вектор конечного продукта
•- оператор управления, преобразующий экзогенный вектор конечного продукта 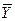 вектор валового продукта
вектор валового продукта 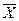 .
.
Из сопоставления кибернетических моделей видно, что для линейной балансовой модели задача, наблюдения и задача управления являются взаимно обратными..Модель управления так же, как и модель наблюдения, является открытой. Эти модели позволяют построить систему взаимосвязанных показателей, но не отвечают на вопрос, 'насколько эффективен тот или иной план. Эту задачу решают оптимизационные модели.
Определим экономическое содержание коэффициентов матрицы (Е-А) 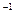 . Для этого распишем покомпонентное векторное равенство
. Для этого распишем покомпонентное векторное равенство
(Е-А) 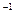
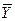 =
= 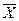 (5.6)
(5.6)
обозначим элементы матрицы (Е-А) 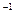 через Cij (i,j = 1,2,…n).
через Cij (i,j = 1,2,…n).
Тогда
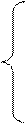 c11 Y1+c12 Y2+ + c1n Yn= X1
c11 Y1+c12 Y2+ + c1n Yn= X1
c21 Y1+c22 Y2+ + c2n Yn= X2
ci1 Y1+ ci2 Y2+ + cin Yn = Xi
cn1 Y1+cn2 Y2+ + cnn Yn = Xn
Положим
 |
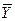
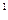 =:
=:
Тогда:
 |  |  |  | ||||

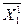 С11 C12 C1n 1 C11
С11 C12 C1n 1 C11
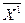 =
= 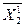 = C21 C22 C2n 0 = C21
= C21 C22 C2n 0 = C21
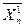 Cn1 Cn2 Cnn 0 Cn1
Cn1 Cn2 Cnn 0 Cn1
характеризует затраты валовой продукции всех отраслей на воспроизводство единицы конечной продукции первой отрасли.
 Положим
Положим
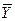
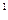 =:
=:
Тогда затраты валовой продукции всех отраслей на воспроизводство единицы конечной продукции второй отрасли составят, соответственно,
 |  |  | |||||
 | |||||||

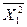 С11 C12 C1n 0 C11
С11 C12 C1n 0 C11
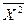 =
= 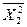 = C21 C22 C2n 1 = C21 (5.9)
= C21 C22 C2n 1 = C21 (5.9)
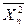 Cn1 Cn2 Cnn 0 Cn1
Cn1 Cn2 Cnn 0 Cn1
а воспроизводство единицы конечной продукции n-й отрасли
 0
0

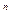 =:
=:
потребует

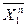 С11 C12 C1n 0 C1n
С11 C12 C1n 0 C1n
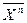 =
= 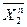 = C21 C22 C2n 0 = C2n (10)
= C21 C22 C2n 0 = C2n (10)
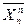 Cn1 Cn2 Cnn 1 Cnn
Cn1 Cn2 Cnn 1 Cnn
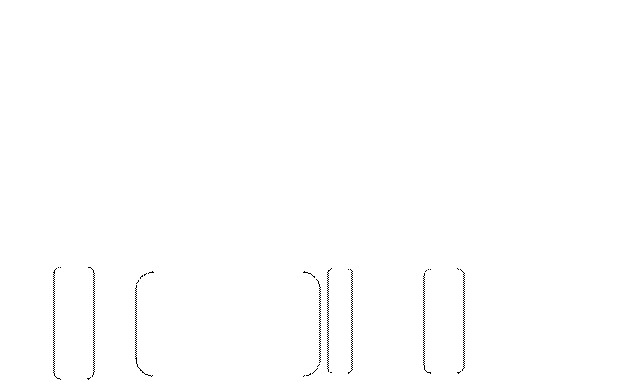
Иными словами, коэффициенты Cij(i,j = 1 2, п) матрицы (Е-А) 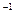 представляют собой коэффициенты полных затрат продукции 1-й отрасли,, идущей на воспроизводство единицы конечной продукции j-й отрасли.
представляют собой коэффициенты полных затрат продукции 1-й отрасли,, идущей на воспроизводство единицы конечной продукции j-й отрасли.
Поставим следующую задачу: как определить валовой выпуск k-й отрасли, необходимый для реализации фиксированного вектора конечного продукта?


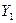
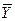 =
= 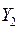
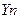
Тогда
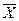 = (Е-А)
= (Е-А) 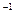
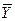
или
 С11 C12 C1n
С11 C12 C1n 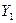
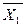
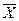 = C21 C22 C2n
= C21 C22 C2n 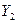 =
= 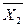 (11)
(11)
Cn1 Cn2 Cnn 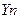
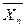

откуда затраты валовой продукции k-й отрасли на воспроизводство фиксированного вектора конечного продукта составят сумму произведений элементов k-й строки матрицы (Е-А) 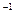 на соот-ветствующие компоненты вектора
на соот-ветствующие компоненты вектора 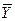 т е:
т е:
Хк=Ск1Yn+Ск2Yn+…+СкnYn, (12),
где к=1,2,…,n.
Задача 1. На плановый год задается матрица коэффициентов прямых затрат
 |
0,3 0,09 0,08
А= 0,08 0,24 0
0,07 0,06 0
и вектор конечного продукта
 153,4
153,4
Y= 17,2
38,4
Построить баланс производства и распределения продукции для трех отраслей Результаты расчетов свести в схему планового межотраслевого баланса. Найти матрицу коэффициентов косвенных затрат К
Решение. Для определения вектора валового продукта и межотраслевых потоков воспользуемся экономико-математической моделью задачи планирования производства и распределения продукции
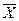 =(Е-А)
=(Е-А) 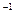
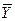
Расчет коэффициентов матрицы полных затрат можно осуществить, кроме прямого обращения матрицы (Е-А), приближенно по формуле
(Е-А) 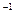 =Е+А+А2+…+Ак+…
=Е+А+А2+…+Ак+…
Получим
 |
1,461 0,182 0,117
(Е-А) 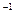 = 0,153 1,334 0,012
= 0,153 1,334 0,012
0,111 0,092 1,009
Найдем вектор валового продукта
 |  |  |
1,461 0,182 0,117 153,4 231,7
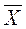 = 0,153 1,334 0,012 17,2 = 46,9
= 0,153 1,334 0,012 17,2 = 46,9
0,111 0,092 1,009 38,4 57,4
Откуда
Х1=231,7
Х2=46,9
Х3=57,4
Определим межотраслевые потоки:
xij= аijXj
Тогда
Х11=69,5; Х12=4,2; Х13=4,6;
Х21=18,5 Х22=11,2; Х23=0;
Х31=16,2; Х32=2,8; Х33=0.
Схема планового межотраслевого баланса будет иметь вид:
| Распределение Производство | Конечный продукт | Валовой продукт | |||
| 1-ая отрасль | 69,5 | 4,2 | 4,6 | 153,4 | 231,7 |
| 2-ая отрасль | 18,5 | 11,2 | 17,2 | 46,9 | |
| 3-ая отрасль | 16,2 | 2,8 | 38,4 | 57,4 | |
| Чистый продукт | 127,5 | 28,7 | 52,8 | ||
| Валовой продукт | 231,7 | 46,9 | 57,4 |

 1,461 0,182 0,117 0,3 0,09 0,08
1,461 0,182 0,117 0,3 0,09 0,08
К=(Е-А) 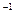 -А; К= 0,153 1,334 0,012 - 0,08 0,24 0 0,111 0,092 1,009 0,07 0,06 0
-А; К= 0,153 1,334 0,012 - 0,08 0,24 0 0,111 0,092 1,009 0,07 0,06 0
 1,161 0,092 0,037
1,161 0,092 0,037
К= 0,073 1,094 0,012
0,041 0,032 1,009
Задача 2..На основании следующих данных рассчитать объемы валового продукта и межотраслевые потоки продукции если известны матрица коэффициентов.прямых материальных затрат А и вектор конечного продукта Y. Заполнить матрицу межотраслевого баланса в стоимостном выражении. Найти матрицу коэффициентов прямых затрат.

 0,3 0,3 0 24
0,3 0,3 0 24
А= 0,2 0,2 0,3 Y= 91
0,1 0,1 0,2 88
Решение. Для определения вектора валового продукта и межотраслевых потоков воспользуемся экономико-математической моделью задачи планирования производства и распределения продукции
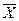 =(Е-А)
=(Е-А) 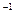
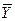
Уравнение решается в следующей последовательности:
1. Рассчитывается матрица (Е-А):
 |  |  |
1 0 0 0,3 0,3 0 0,7 -0,3 0
А= 0 1 0 - 0,2 0,2 0,3 = -0,2 0,8 -0,3
0 0 1 0,1 0,1 0,2 -0,1 -0,1 0,8
2. Рассчитывается обратная матрица (Е-А)-1
 |
1,649 0,649 0,243
(Е-А)-1= 0,514 1,514 0,568
0,27 0,27 1,351
3. Зная матрицу (Е-А)-1, можно рассчитать вектор валового продукта по формуле:
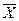 =(Е-А)
=(Е-А) 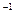
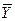
 |  |  |
1,649 0,649 0,243 24 120
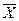 = 0,514 1,514 0,568 * 91 = 200
= 0,514 1,514 0,568 * 91 = 200
0,27 0,27 1,351 88 150
Межотраслевые материальные потоки: xij рассчитываются по формуле:
xij= аijXj
Тогда x11=а11*Х1=0,3*120=36
x12=а11*Х2=0,3*200=60
x12=а13*Х3=0
x21=а21*Х1=0,2*100=24
x22=а22*Х2=0,2*200=40
x23=а23*Х3=0,3*150=45
x31=а31*Х1=0,1*120=12
x32=а32*Х2=0,1*200=20
x33=а33*Х3=0,2*150=30
Компоненты вектора – чистого продукта находятся по формуле:
Z1=X1-(x11+ x21+ x31)=120-(36+24+12)=48
Z2=X2-(x12+ x22+ x32)=200-(60+40+20)=80
Z3=X3-(x13+ x23+ x33)=150-(0+45+30)=75
Таблица МОБ для данного примера будет иметь вид:
| Распределение Производство | Конечный продукт | Валовой продукт | |||
| 1-ая отрасль | |||||
| 2-ая отрасль | |||||
| 3-ая отрасль | |||||
| Чистый продукт Z | |||||
| Валовой продукт |
Date: 2015-06-11; view: 1226; Нарушение авторских прав