Тема 7. Управление запасами

Фирмы часто делают различные запасы. Хранятся сырье, заготовки, готовая продукция, предназначенная для продажи.

Запасов не должно быть ни слишком много, ни слишком мало. В первом случае возникает необходимость неоправданных затрат на хранение, на амортизацию товара. Во втором случае может оказаться так, что на складе не будет нужного товара. Кроме того, малое количество запасов подразумевает их частое пополнение, что также требует затрат.

Задача управления запасами состоит в том, чтобы избежать обеих крайностей и сделать общие затраты по возможности меньше. Отметим, что в целом эта область науки управления развита довольно хорошо, разработаны многочисленные модели с применением различных математических методов. Мы рассмотрим несколько простейших детерминированных моделей управления запасами.

7.1. Основная модель

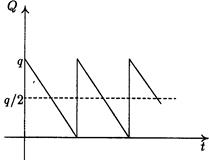
Важнейшую роль в наших рассмотрениях будет играть функция изменения запаса. Это связь между количеством единиц товара на складе (обозначим его через Q ) и временем t. Будем считать, что имеется один вид товара.

Если на товар имеется спрос, то функция изменения запаса Q = Q{t} убывает. Если товар, наоборот, завозят на склад, то эта функция возрастает. Мы будем считать возможным мгновенное пополнение запаса.

Затраты, связанные с запасами, можно разделить на три части.

А. Стоимость товара.

Б. Организационные издержки. Это расходы, связанные с офор­млением товара, его доставкой, разгрузкой и т. д.

В. Издержки на хранение товара. Это затраты на аренду 'склада амортизацию в процессе хранения и т. д.

Рассмотрим основные величины и предположения относительно них принятые в рамках основной модели. Мы будем в основном использовать в качестве единицы измерения денежных средств условные единицы (УЕ), это могут быть рубли, доллары и т. п.; в качестве единицы измерения времени — год, хотя можно было бы взять месяц, квартал и т. п.

1. Цена единицы товара — С УЕ. Цена постоянна, рассматривается один вид товара.

2. Интенсивность спроса ,— d единиц товара в год. Будем считать, что спрос постоянный и непрерывный.

3. Организационные издержки— S УЕ за одну партию товара. Бу­дем считать, что организационные издержки не зависят от размера поставки, т. е. от количества единиц товара в одной партии.

4. Издержки на хранение запаса — h УЕ на единицу товара в год. Будем считать эти издержки постоянными.

5. Размер одной партии товара постоянен — q единиц. Партия поступает мгновенно в тот момент, когда возникает дефицит, т. е. когда запас на складе становится равным нулю.

При сделанных предположениях график функции изменения запаса будет таким, как показано на рис. 1: он состоит из повторяющихся циклов пополнения запаса между двумя соседними дефицитами. Вертикальные отрезки отвечают мгновенному пополнению запаса.

Параметры с, d, s, h считаются заданными. Задача управления запасами состоит в выборе параметра q таким образом, чтобы минимизировать годовые затраты.

Для решения сформулированной задачи надо преждевсего выразить эти затраты через параметры с, d, s, h, q.

А. Поскольку годовая интенсивность спроса равна d, а цена единицы товара — с, то общая стоимость товара в год равна

С d

Б. Поскольку в одной партии q единиц товара, а годовой спрос равен d, то число поставок равно d/q. В течение года организационные издержки равны

S (d/q)

В. Средний уровень запаса равен отношению площади под графиком за цикл, к продолжительности цикла. Этот средний уровень, равен q/2 (на рис. 3 обозначен пунктиром). Поскольку годовые издержки на хранение единицы товара равны h, то общие издержки на хранение составляют

h (q/2)

Рис. 4 Рис. 5

Таким образом, общие издержки С вычисляются по формуле

С(q)=с d+S (d/q)+h (q/2)

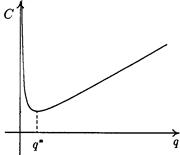
Еще раз напомним, что в рамках модели параметры с, d, s, h счи­таются заданными и требуется найти такое число q*, чтобы функция С = C(q) принимала наименьшее значение на множестве q > 0 именно в точке q*.

График функции С = C(q) показан на рис. 5

Для нахождения точки q* минимума функции С = C(q) найдем ее производную (с, d, s, h — фиксированные числа):

C’(q) = h/2- S (d/q²)

приравнивая C'(q) к нулю, получаем

S (d/q²)= h/2

Отсюда можно найти q*. Имеем:

q*=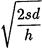

Полученная формула называется формулой оптимального запаса или формулой Харриса (Harris).

Пример 7.1. Пусть интенсивность равномерного спроса составляет 1000 единиц товара в год. Организационные издержки равны 10 УЕ, издержки на хранение — 4 УЕ на единицу товара в год, цена товара — 5 УЕ. Определить оптимальный размер партии в предположении, что система подчиняется основной модели.

Решение.

Имеем: d=1000, s =10, h =4, с =5.

Общие затраты равны: С(q)=с d+S (d/q)+h (q/2)

C{q) = = 5000 +10000/q+2q

Тогда

C’{q) =-10000/(q²)+2,

а оптимальный размер поставки q* является решением уравнения

-10000/(q²)+2=0,

Т е.. q*=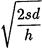

q*= 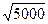= 71

Замечание. Найдя оптимальный размер заказа, можно определить оптимальное число поставок за год n* и соответствующую продол­жительность цикла изменения запаса t*:

n*=1000/71=14

t*=365/14=26

7.2. Модель производственных поставок

В основной модели предполагалось, что поступление товаров на склад происходит мгновенно. Это предположение достаточно хорошо отражает ситуацию, когда товар поставляется в течение одного дня (или ночи). Если товары поставляются с работающей производственной линии, необходимо модифицировать основную модель В этом случае к параметрам с, d, s, h добавляется еще один — производительность производственной линии р (единиц товара в год) Будем считать ее заданной и постоянной.

Эта новая модель называется моделью производственных поставок. Величина q по-прежнему обозначает размер партии. В начале каждого цикла происходит "подключение" к производственной линии, которое продолжается до накопления q единиц товара. После этого пополнения запасов не происходит до тех пор, пока не возник дефицит.

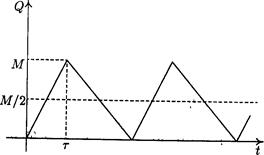
Рис. 6

График функции изменения запаса имеет вид, изображенный на рис.6. Общие издержки C(q), как и в основной модели, состоят из трех частей.

А. Общая стоимость товара в год равна

С d

Б. Годовые организационные издержки равны

S (d/q)

В. Издержки на хранение вычисляются следующим образом. Пусть — время поставки (рис. 3). В течение этого времени происходит как пополнение (с интенсивностью р), так и расходование (с интенсивностью d ) запаса. Увеличение запаса происходит со скоростью (p—d ), поэтому достигнутый к концу периода пополнения запаса максимальный его уровень М вычисляется по формуле

M=(p-d) (заметим, что М < q ). Однако,

Р = q

(за время при интенсивности производства р произведено q единиц товара). Из последних двух равенств следует, что

M=(p-d) (q/p)

Средний уровень запаса, как и в основной модели, равен половине максимального, т. е. М/2. Таким образом, издержки на хранение запаса равны

((p-d) q h)/2p

Общие издержки вычисляются по формуле

С(q)=с d+S (d/q)+ ((p-d) q h)/2p

C’(q) =((p-d) h)/2 p - S (d/q²)

Оптимальный размер поставок q* получаем из уравнения

S (d/q²)= =((p-d) h)/2 p

Имеем:

q*=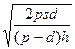

Пример 7.2. Интенсивность равномерного спроса составляет 1000

единиц товара в год. Товар поставляется с конвейера, производительность которого составляет 5 тыс. единиц в год. Организационные издержки равны 10 УЕ, издержки на хранение — 2 УЕ, цена единицы товара — 5 УЕ

Чему равен оптимальный размер партии?

Решение.

Имеем: d = 1000, р = 5000, s = 10, h = 2, с = 5.

Далее, q*= 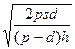= =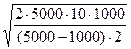112

Замечание. Найдя оптимальный размер заказа, можно определить оптимальное число поставок за год n* и соответствующую продолжительность поставки *, и продолжительность цикла пополнения запаса t*:

n*=1000/112=9

*=q*/p=356*112/5000=8

t*=365/9=41

7.3. Модель поставок со скидкой

Рассмотрим ситуацию, описываемую в целом основной моделью, но с одной особенностью, которая состоит в том, что товар можно поставлять по льготной цене (со скидкой), если размер партии достаточно велик. Иными словами, если размер партии q не менее заданного числа q_o, товар поставляется по цене c₀, где c₀ < c.

Функция общих издержек C(q) задается в таком случае следующим образом:

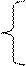С(q)=с d+S (d/q)+h (q/2)

С(q₀)=с₀ d+S (d/q)+h (q/2)

Нетрудно видеть, что функция C(q) в точке q = q_o разрывная.

Обе функции имеют минимум в точке, где производная равна 0.

C'(q) = h/2- S (d/q²)

приравнивая C'(q) к нулю, получаем

S (d/q²)= h/2

Отсюда можно найти q*.

Имеем: q*=

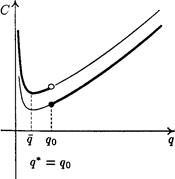
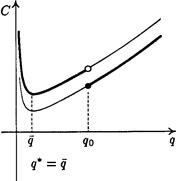
Для выяснения вопроса о том, какой размер партии оптимален, следует сравнить значения функции C(q) в точках q и q_o, и та точка, где функция C(q) принимает меньшее значение, будет оптимальным размером партии q* в модели поставок со скидкой (см. рис. 7, 8).

Рис. 7 Рис. 8

Замечание. Может случиться так, что С(q)= С(q₀). Тогда, разумеется, q _o = q = q*.

Пример 3. Предположим, что интенсивность равномерного спроса составляет 1000 единиц товара в год. Организационные издержки равны 10 УЕ, издержки на хранение — 4 УЕ. Цена единицы товара равна 5 УЕ, однако, если размер партии не менее 500 единиц цена снижается до 4 УЕ. Найти оптимальный размер партииq*.

Р ешени е. Здесь

d=1000, s =10, h =4, с =5, q_o = 500, с_o = 4. Общие издержки определяются функцией C(q).

C(q)= 5000 + 10000/q + 2q, при q < 500,

C(q_o) = 4000+10000/q + 2q, при q > 500,

Найдем точку локального минимума.

Имеем:. q*=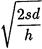

q*= 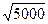= 71

Поскольку q* < 500, то

C(q*) = 5283.

В точке q = q_o получаем

C(qo)=5020.

Таким образом,

q * = 500.

Date: 2015-06-11; view: 3671; Нарушение авторских прав