
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Тема 4. Транспортная задача
|
|
Под транспортной задачей понимают целый комплекс задач, имеющих определенную специфическую структуру. Простейшими из таких задач являются задачи о перевозках некоторого продукта (однородного груза) из пунктов отправления в пункты назначения при минимальных затратах на перевозки.
Обычно начальные условия записываются в исходную транспортную таблицу:
| Поставщики Аi | Мощность поставщиков | Потребители и их спрос, Bj | |||||
| ... | j | ... | l | ||||
| N1 | N2 | ... | Nj | ... | Nj | ||
| M1 | a11 | a12 | ... | a1j | ... | a1j | |
| x11 | x12 | x1j | x1l | ||||
| M2 | a21 | a22 | ... | a2j | ... | a2l | |
| x21 | x22 | x2j | x2l | ||||
| ... | ... | ... | ... | ... | ... | ... | ... |
| i | Mi | ai1 | ai2 | ... | aij | ... | ail |
| ... | xi1 | xi2 | xij | ... | xil | ||
| k | Mk | ak1 | ak2 | ... | akj | ... | akl |
| xk1 | xr2 | xkj | xkl |
В таблице aij означают затраты на перевозку одной единицы груза от i - го поставщика (i=1,2,...,k) к j - му потребителю (j=1,2,...l), Mi - мощность i-го поставщика в планируемый период, Nj - спрос j -го потребителя в этот же период.
Обозначим xij количество груза, которое нужно перевезти от i -го поставщика к j -му потребителю. Математическая модель задачи сведется к нахождению минимума функции цели, выражающей суммарные затраты на перевозки груза, т.е. функции F= 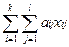 при следующих ограничениях:
при следующих ограничениях:
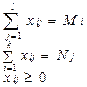
Решение транспортной задачи может быть найдено так называемым распределительным методом.
Задача 4. Исходная таблица транспортной задачи:
| Поставщики | Мощность поставщиков | Потребители и их спрос | |||
| B 1 | B 2 | B 3 | B 4 | ||
| A1 | |||||
| A2 | |||||
| A3 |
Методические указания к решению
Задачи, в которых SAi= S Bj, называются закрытыми. Если это условие не выполняется, то задача открытая, и ее необходимо сделать закрытой, добавив соответственно фиктивного поставщика или потребителя со стоимостями перевозок равными 0.
Поскольку SAi=50+70+80=200, а S Bj = 20+100+60+50=230, следует ввести дополнительного, фиктивного поставщика мощностью 30.
После этого следует определить исходный (отправной) план перевозок любым из двух методов: метод северо-западного угла; метод минимального элемента. Покажем применение каждого из этих методов.
Метод северо-западного угла
Закрытая задача, к которой приведена исходная, имеет таблицу:
| Поставщики | Мощность поставщиков | Потребители и их спрос | |||||||
| B 1 | B 2 | B 3 | B 4 | ||||||
| A1 | |||||||||
| A2 | |||||||||
| A3 | |||||||||
| A4 |
Последовательно заполняем объемы поставок, начиная с верхнего левого угла (северо-западного). Затем проверяем баланс (суммы по колонкам и столбцам). Если план построен правильно, то для каждой свободной клетки можно построить цикл, т.е. замкнутый контур с прямыми углами, такой, чтобы начинаясь в свободной клетке, он проходил через заполненные клетки. Вид этого контура может быть различным. Например:
 Кроме того, число занятых клеток должно быть m+n -1.
Кроме того, число занятых клеток должно быть m+n -1.
В данном случае это условие не соблюдается - число занятых клеток должно быть 4+4-1=7, а в таблице их только 6. Следует в любую пустую клетку вписать 0, выбирая сначала клетки с минимальными стоимостями, но так, чтобы для нее нельзя было построить цикл. В нашем случае нельзя вписать в клетки A2B1 и A4B3, а во все остальные - можно. Выберем клетку со стоимостью 1 A2B3. Теперь в таблице 7 заполненных клеток.
Затем считают общие затраты на перевозку как сумму произведений количества груза на стоимость перевозки единицы груза:
S= 20*1+ 30*3+70*5+ 0*1+60*3+20*4+30*0=720 (руб)
Date: 2015-06-11; view: 926; Нарушение авторских прав