Практическая реализация методов нелинейного программирования

Для решения практической задачи оптимизации создает­ся ее математическая модель. При этом стремятся обеспе­чить ее максимальное приближение к действительности, а вопрос о том, как будут проводиться оптимизационные расчеты, откладывается до момента, когда модель построе­на.

Прежде чем приступить к решению задачи при уже по­строенной математической модели, эту модель нужно про­анализировать с точки зрения организации будущего вы­числительного процесса и по возможности предотвратить его осложнения. Например, целевая функция выражена квадратичной формой с диагональной матрицей:

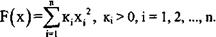
Если численные значения K_i существенно различны, то поверхности уровня функции F(x) вытянуты по тем коорди­натным осям, которым соответствуют малые значения K_i. Возникает овражность, существенно замедляющая сходи­мость многих алгоритмов оптимизации. В данном случае этой овражности легко избежать с помощью замены переменных y_i = ki^1/2x_i. После этой замены целевая функция превращается в сумму квадратов, а поверхности уровня в сферы. При наличии ограничений в них тоже необходимо про­извести замену переменных.

Для функции произвольного вида можно взять приближенные значения вторых производных d²F(x)/dx_i², если эти производные легко доступны для вычисления и не сильно меняются в допустимой области. При этом не получим сферических поверхностей, но существенно уменьшим овражность.

Масштабирование заменой переменных с вычислитель­ной точки зрения имеет своей целью добиться, чтобы в об­ласти поиска приходилось иметь дело с переменными, аб­солютные величины которых имеют одинаковые порядки. Если в области поиска модули переменных существенно меняются, то такая замена ненадежна.

Если для каждой переменной известен диапазон измене­ния, например в явном виде заданы ограничения a_i <= x_i <= b_i, то имеет смысл, как говорят, «отмасштабировать и центрировать переменные». Это означает переход к новым переменным у, по формуле

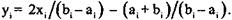
После этой замены все новые переменные у_i окажутся на отрезке [-1,1]. Иногда такое преобразование называют пе­реходом к безразмерным центрированным величинам. По­сле оптимизации по у_i исходные переменные x_i определя­ются с помощью обратного преобразования:

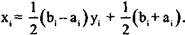
Или в матричном виде х = Dy + с, где D — диагональная матрица с элементами d_ij = 1/2 (b_i – а_i), а с — вектор с ком­понентами с_i= 1/2 (b_i + a_i). Если градиент по старым пере­менным х_i обозначить как обычно g, то градиент по новым переменным g_y = Dg.

Существенные сложности при решении задач оптимиза­ции возникают при наличии негладких функций. Разрабо­танные в недавнем прошлом специальные методы неглад­кой оптимизации достаточно сложны. В то же время в практических целях функции с разрывными производными часто могут с успехом быть заменены функциями, имеющими непрерывные производные.

В программных реализациях стремятся избежать рабо­ты с величинами, численные значения которых различа­ются на много порядков, чтобы уменьшить влияние оши­бок представления чисел в компьютере.

Существенных упрощений процесса оптимизации в ряде случаев можно добиться преобразованием целевой функции н ограничений при введении дополнительных переменных. Наиболее наглядно это проявляется в задаче минимизации суммы модулей линейных функций при линейных ограни­чениях. Задача имеет вид: найти min Σ|η(x)| при огра­ничениях Ах <= b. Здесь

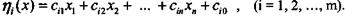
Дополнительные переменные y_i вводятся так: | η(x)| <= у_i. При этом появляются 2m дополнительных линейных неравенств: 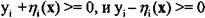относительно n исходных и m дополнительных перемен­ных, но целевая функция приобретает простой вид 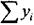, так что исходная задача с негладкими функциями сводится к задаче линейного программирования.

Вопросы для самоконтроля:

1.Необходимые и достаточные условия первого и второго порядков оптимальности в задаче с ограничениями-равенствами.

2.Необходимые и достаточные условия первого и второго порядков оптимальности в задаче со смешанными ограничениями

Рекомендуемая литература:

1.Ашманов С.А. Линейное программирование. —М.: Наука, 1981.

2.Айсагалиев А.С., Айсагалиева С.С. Лекции по методам оптмизации.-Алматы:Гылым,1996

Date: 2015-07-10; view: 498; Нарушение авторских прав