Теорема о линейном представлении наибольшего общего делителя

Теорема. Если 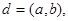то существуют целые числа и и v, для которых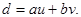

Доказательство: Рассмотрим множество всех целых чисел вида 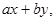где х и у - любые целые числа

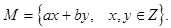
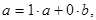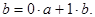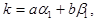
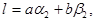
Это множество не пусто, в частности, ему принадлежат числа а и b. Ведь а можно представить в виде а b - в виде Для любых двух целых чисел из этого множества частное от деления одного на другое также принадлежит множеству М. Действительно, если 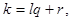то

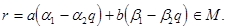
Пусть 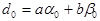- наименьшее положительное число в множестве М. Тогда любое число из М делится на число 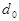без остатка. Действительно, остаток должен принадлежать множеству М и должен быть меньше 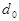, а этому условию удовлетворяют лишь остатки, равные нулю.

Таким образом, и а, и b делятся на 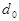без остатка, т.е. 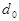– их общий делитель. Очевидно, что 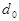делится на любой другой их общий делитель, а это означает, что ■

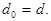Пример. Найти линейное представление наибольшего общего делителя чисел 1173 и 323.

Решение: Из примера, приведенного в предыдущем параграфе, известно, что НОД(1173, 323) = 17. Будем подниматься по равенствам алгоритма Евклида вверх:

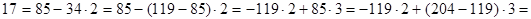
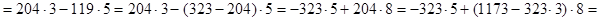
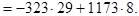
Ответ: НОД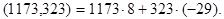

Теорема Евклида. Если ас делится на b, с и b взаимно просты, то а делится на b.

Доказательство: Так как 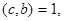то по теореме о линейном представлении НОД существуют числа и и v, для которых

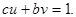
Тогда

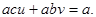
Из условия следует, что слагаемое аси делится на b, слагаемое ab n также делится на b. Отсюда, а делится на b. Что и требовалось доказать. ■

Date: 2015-07-02; view: 14540; Нарушение авторских прав