
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Теория делимости
|
|
Модуль 1. Элементы теории чисел
Глава 1.1. Целые числа
Теория делимости
Целыми называются числа..., -3, -2, -1, 0, 1, 2, 3,..., т.е. натуральные числа 1, 2, 3, 4,..., а также нуль и отрицательные числа -1, -2, -3, -4,.... Множество всех целых чисел обозначается через Z (от немецкого слова Zahl – число).
Сумма, разность и произведение двух целых чисел – также целые числа. Если для трех целых чисел a, b и с выполнено равенство  то говорят: а делится на b или b делит а и применяют соответственно обозначения
то говорят: а делится на b или b делит а и применяют соответственно обозначения 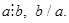 При этом а называют кратным числа b, а b – делителем числа а.
При этом а называют кратным числа b, а b – делителем числа а.
Свойства делимости целых чисел:
1) а делится на а (рефлексивность);
2) если а делится на b, b делится на а, то 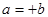 или - b;
или - b;
3) если а делится на b, b делится на с, то а делится на с (транзитивность);
4) если 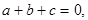 а делится на d, b делится на d, то и с делится на d;
а делится на d, b делится на d, то и с делится на d;
5) если ad делится на bd, 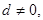 то а делится на b.
то а делится на b.
Доказательство свойства 1: 
Доказательство свойства 2: 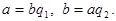 Отсюда
Отсюда 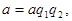 т.е.
т.е. 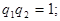
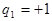 или -1.
или -1.
Доказательство свойства 3: 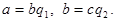 Отсюда
Отсюда 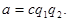
Доказательство свойства 4: 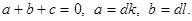 Отсюда
Отсюда 
Доказательство свойства 5: 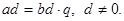 Отсюда
Отсюда 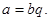
Теорема (о делении с остатком): Для любых двух целых чисел а и b существует и притом единственная пара чисел q и r, для которых
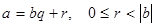 .
.
Доказательство теоремы существования. Расположим на числовой оси числа..., -2 b, - b, 0, b, 2 b,...
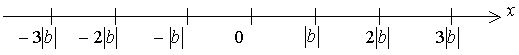
Они разбивают ось на интервалы длины 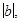 в один из которых попадает число а, т.е. существует целое число q, для которого
в один из которых попадает число а, т.е. существует целое число q, для которого
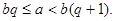
Введем обозначение 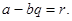 Тогда
Тогда
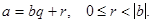
Доказательство теоремы единственности проведем методом от противного. Пусть существуют два представления
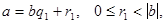 (1)
(1)
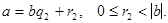 (2)
(2)
Предположим, что 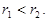 Тогда
Тогда 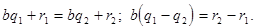 Здесь
Здесь 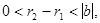 в то же время
в то же время 
 Получили противоречие, а это значит, что предположение
Получили противоречие, а это значит, что предположение 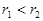
 неверно. Аналогично приводит к противоречию предположение
неверно. Аналогично приводит к противоречию предположение 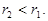 Остается лишь одна возможность
Остается лишь одна возможность  но тогда и
но тогда и 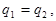 т.е. оба представления совпадают.
т.е. оба представления совпадают.
Доказательство закончено. ■
Число q в равенстве 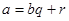 называется неполным частным, а r остатком от деления а на b. Если
называется неполным частным, а r остатком от деления а на b. Если 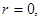 то q называется частным от деления а на b.
то q называется частным от деления а на b.
Пример. Если  то
то 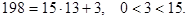
Если  то
то 
Если 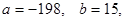 то
то 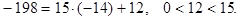
Если 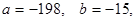 то
то 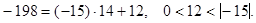
Если 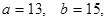 то
то 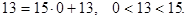
Date: 2015-07-02; view: 959; Нарушение авторских прав