Синхронный двигатель как элемент системы автоматического регулирования

Базой для анализа синхронного двигателя как объекта регулирования является аналитическая теория синхронной машины и элементы теории обобщенной электрической машины. Для анализа электрических машин, симметричных в магнитном отношении (АД, синхронные неявнополюсные машины) может быть рассмотрена обобщенная машина, которая представляет собой двухфазную машину, имеющую по две обмотки на статоре и роторе, расположенные в ортогональных осях. Оси статора б-b неподвижны, оси ротора d-q вращаются со скоростью w.

Дифференциальные уравнения контуров обобщенной машины записываются следующим образом

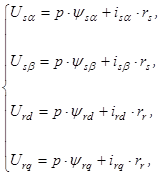
где 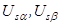– напряжение, прикладываемое к обмотке статора;

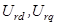– напряжение, прикладываемое к обмотке ротора;

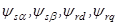– потокосцепление обмоток статора и ротора;

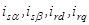– токи контуров статора и ротора;

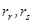– активные сопротивления ротора и статора.

Так как данные уравнения напряжений контуров машины являются дифференциальными уравнениями с переменными коэффициентами, то это практически исключает их использование для построения структурных схем электродвигателей как объектов регулирования.

Поэтому есть необходимость перейти к нелинейным дифференциальным уравнениям с постоянными коэффициентами. Для этой цели применяются линейные преобразования, которые заключаются в преобразовании исходных уравнений к другим координатам, т.е. в изменении координат отсчета переменных при условии обеспечения инвариантности мощности. Линейным преобразованиям подвергаются все переменные машины (u, i, 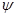). На рисунке 5.2.1 изображены векторные диаграммы обобщенной машины для прямого преобразования координат.

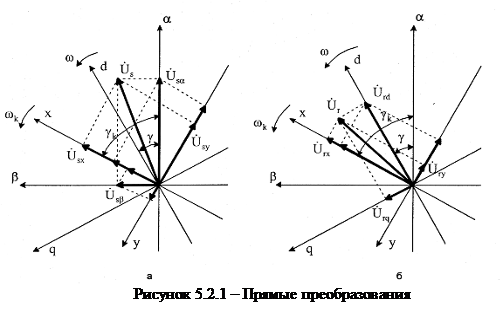
Прямые преобразования координат от осей б-в, d-q к осям x-y, вращающихся с произвольной скоростью 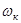, осуществляются в соответствии с векторными диаграммами на рисунке 5.2.1 по следующим соотношениям

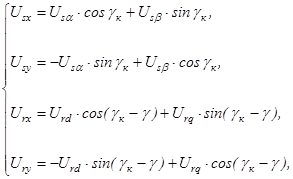
где 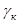– координатный угол между осями б-x;

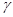– угол между осью d и осью б.

В синхронной машине целесообразно рассматривать систему координат, вращающуюся вместе с ротором (ось х при этом совмещают с осью б). Это так называемая система осей d-q (рис. 5.2.2).

В системе координат d-q выражения для потокосцеплений не содержат переменных индуктивностей, а дифференциальные уравнения напряжений при неизменной частоте вращения машины имеют постоянные коэффициенты, что существенно облегчает исследование динамики привода.

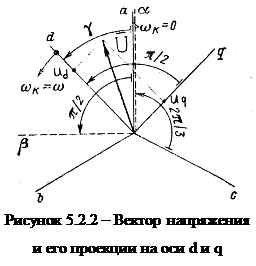
Преобразование к осям d-q является практически единственным, приводящим дифференциальные уравнения синхронной машины с периодическими коэффициентами к уравнениям с постоянными коэффициентами. Поэтому в теории синхронной машины преобразование к осям d-q имеет фундаментальное значение.

Преобразование к осям d-q производится в соответствии с уравнениями:

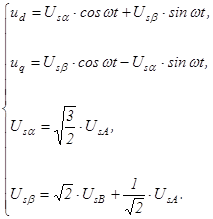
Аналогичные выражения можно записать для токов и потокосцеплений по осям d и q.

Напряжения u_d и u_q называют, соответственно, продольным и поперечным напряжением статора. Угол 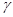определяется угловым положением ротора относительно результирующего вращающегося потока статора и, по сути, является углом нагрузки 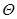синхронной машины. В переходных процессах этот угол изменяется с изменением скорости вращения двигателя.

Построение структурной схемы осуществляется в соответствии со следующими уравнениями.

Уравнения равновесия напряжений статора

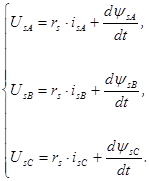
Потокосцепления статора

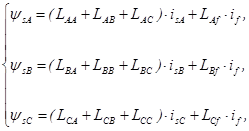
где i_f – ток обмотки возбуждения;

L_AA, L_AВ, L_AС, L_ВA, L_ВВ, L_ВС, L_СA, L_СВ, L_СС – индуктивности статора;

L_Af, L_Вf, L_Сf – взаимные индуктивности фаз статора и обмотки возбуждения.

Потокосцепление обмотки возбуждения

,

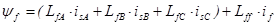где L_ff – собственная индуктивность обмотки возбуждения.

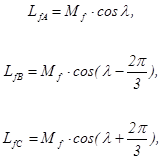
где M_f – максимальное значение взаимной индукции.

Преобразование токов статора к осям d-q осуществляется в соответствии с выражениями

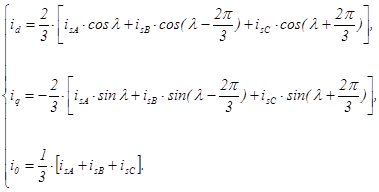
где i₀ – ток нулевой последовательности.

Система уравнений в результате преобразований примет следующий вид

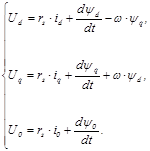
Аналогично выражения для потокосцеплений примут вид

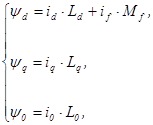
где , , ;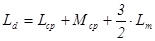

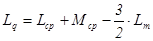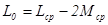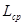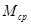, – средние значения собственной индуктивности фазы статора и взаимной индуктивности между двумя фазами статора.

Потокосцепление ротора

.

Напряжение обмотки ротора

.

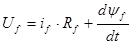Электромагнитный момент синхронного двигателя в осях d-q

.

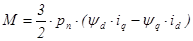Уравнение движения привода

.

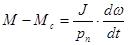Приведенные уравнения образуют полную систему уравнений синхронного двигателя. Преобразовав ее к виду удобному для синтеза САР, получим следующие выражения.

,

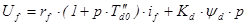где , , .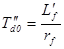

,

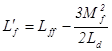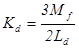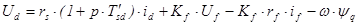где , , .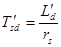

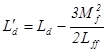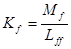Потокосцепление статора по продольной оси

.

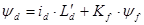Операторным и алгебраическим уравнениям соответствует структурная схема СД, приведенная на рисунке 5.2.3. Анализ показывает, что СД представляет собой нелинейный многосвязный объект с наличием внутренних перекрестных обратных связей. В частности, в контурах токов статора имеются внутренние обратные связи по ЭДС вращения 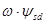и 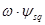, которые определяют взаимное влияние продольных и поперечных контуров машины.

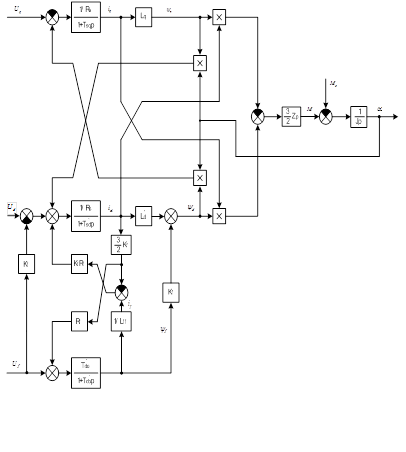
Рисунок 5.2.3 – Структурная схема синхронного двигателя в системе отсчета, ориентированной по ротору

Date: 2015-07-02; view: 1237; Нарушение авторских прав