Принципы построения систем управления двигателями переменного тока

В соответствии с векторными диаграммами и соотношениями между основными параметрами двигателя переменного тока, изученными в предыдущих курсах, его электромеханические свойства при фиксированной частоте питания однозначно определяются как абсолютными значениями магнитных потоков, потокосцеплений и токов цепей машины, так и их векторными взаимосвязями. Отсюда и различные принципы управления двигателем переменного тока (АД или СД):

- скалярный, при котором осуществляется регулирование лишь абсолютных значений переменных двигателя;

- векторный, при котором одновременно осуществляется принудительная взаимная ориентация векторов переменных двигателя в соответствии с принятым законом регулирования.

При этом управляемость двигателем может обеспечиваться совместным управлением либо частоты и напряжения 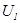, либо частоты и тока 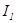статорной обмотки. Первый способ управления принято называть частотным управлением, а второй – частотно-токовым управлением. Выбор способа и принципа управления определяется совокупностью статических, динамических, энергетических и затратных требований к электроприводу.

Скалярный принцип частотного управления является наиболее распространенным в переменном электроприводе. Ему свойственна техническая простота измерения и регулирования абсолютных значений переменных двигателя. Однако реализация желаемых законов регулирования скорости и момента двигателя, их стабилизация и ограничение, при которых обеспечивалось бы постоянство или ограничение в допустимых пределах внутренних переменных СД (тока статора, потокосцеплений, основного магнитного потока), из-за сложных функциональных зависимостей между ними весьма ограничена [15]. И если в статических режимах за счет комбинаций обратных связей по переменным двигателя в замкнутых системах частотного регулирования и можно добиться желаемых или близких к ним свойств электропривода, то в динамических режимах эта задача трудно выполнима. Связано это с достаточно сложными электромагнитными процессами, протекающими в СД.

Векторный принцип основан на принудительной взаимной ориентации векторов потокосцеплений и токов двигателя в полярной или декартовой системе координат в соответствии с заданным законом регулирования. В замкнутых системах векторного управления по цепям обратных связей наряду с абсолютными значениями регулируемых переменных поступает информация о текущем пространственном положении их векторов. За счет регулирования модулей переменных и углов между их векторами обеспечивается полное управление двигателем как в статике, так и в динамике, обеспечивая тем самым заметное улучшение качества переходных процессов по сравнению со скалярным управлением.

В связи с тем, что к проектируемому электроприводу клети прокатного стана предъявляются весьма жесткие требования по обеспечению качественных переходных процессов во всех режимах работы, система управления приводным синхронным электродвигателем должна быть организована по векторному принципу регулирования.

Информация о текущих значениях модуля и пространственного положения векторов переменных СД может быть получена как прямым их измерением с помощью соответствующих датчиков, так и косвенно на основе математической модели двигателя. Конфигурация и сложность такой модели определяются техническими требованиями к электроприводу. При сложности вычислительных операций и алгоритмов управления электроприводом достоинство систем с косвенным регулированием – в простоте технических решений и, соответственно, в практической надежности. Поэтому в современных и наиболее совершенных частотно-регулируемых электроприводах, где системы программного управления реализованы на основе микропроцессорной техники, информация о векторах потокосцеплений электрической машины получается косвенным путем на основе ее математических моделей.

Вариант частотно-токового векторного управления является наиболее распространенным, поскольку при регулировании тока обеспечивается регулирование момента, независимо от частоты питающего напряжения двигателя, что упрощает схему управления, а также одновременно достаточно просто обеспечивает ограничение перегрева двигателя.

Система векторного управления СД в общем случае должна решать задачи регулирования и стабилизации момента и скорости двигателя. Электромагнитный момент в машине переменного тока можно представить как результат взаимодействия магнитных полей, создаваемых токами, протекающими по обмоткам статора и ротора. Выражение для электромагнитного момента СД в векторной форме имеет следующий вид

,

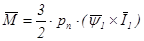где p_n – число пар полюсов СД;

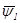- вектор потокосцепления статора;

– вектор тока статора.

Вектор потокосцепления статора может быть записан в следующей форме

,

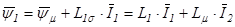где 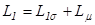– полная индуктивность цепи статора СД;

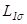– индуктивность рассеяния обмотки статора;

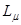– взаимоиндуктивность.

В соответствии с двумя последними выражениями, формирование момента СД возможно за счет воздействий на абсолютные значения векторов потокосцеплений 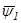, , 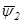, 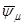токов 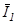, 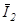и фазовых сдвигов между ними. От того, какие вектора выбраны в качестве регулируемых будет зависеть принцип построения и техническая реализация системы управления электроприводом. Если воспользоваться выражением

,

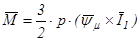то в качестве регулируемых будут выбраны вектора 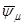и .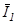

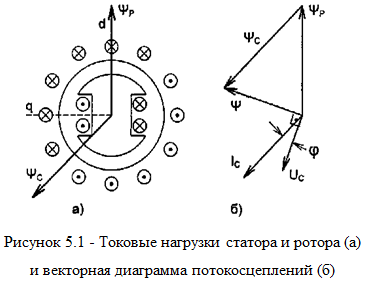
На рис. 5.1, а изображен в разрезе синхронный двигатель с нанесенными на ротор и статор токовыми нагрузками и соответствующими им потокосцеплениям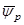и и 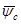, которые изображены в виде пространственных векторов. Здесь же нанесена система прямоугольных координат, жестко связанная с ротором (оси d и q). Причем одна из осей (ось d) направлена вдоль оси катушки ротора, а другая (ось q) – поперек. Когда на трехфазную обмотку статора подано трехфазное напряжение, токи проводников обмотки статора создают вращающееся магнитное поле, которое увлекает за собой ротор.

На рис. 5.1, б изображена упрощенная векторная диаграмма, построенная в предположении, что в двигателе нет потоков рассеяния и отсутствует падение напряжения в цепи обмоток статора. Вектор результирующего потокосцепления двигателя (потокосцепления в воздушном зазоре) равен геометрической сумме составляющих 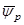и 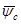. Составляющая 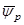направлена по оси d. Направление и величина вектора 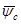определяются мгновенными значениями токов фазных обмоток статора. В основу векторного принципа регулирования положено известное из теории электрических машин выражение для электромагнитного момента

,

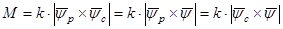где k = 0,5 m / L_m – коэффициент пропорциональности;

m – число фаз двигателя;

L_m - индуктивность тока намагничивания.

Если сопоставить это выражение с векторной диаграммой потокосцеплений в электрической машине (рис. 5.1, б), то площадь S_D, ограниченная векторами-слагаемым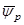и и 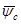и вектором-суммой (площадь моментного треугольника в электрической машине), пропорциональна величине электромагнитного момента, т.е.

.

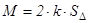Таким образом, с учетом сказанного можно так сформулировать первое правило векторного регулирования электромагнитного момента: чтобы косвенным способом регулировать величину электромагнитного момента в электрической машине, достаточно каким-либо способом изменить площадь моментного треугольника, т.е. векторного треугольника, соответствующего выражению

.

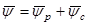В регулируемом электроприводе переменного тока наблюдается избыточность управляющих воздействий, поэтому одно и то же значение момента и скорости электродвигателя, требуемое по условиям ведения технологического процесса, может быть реализовано при разных электромагнитных состояниях электродвигателя, соответствующих моментным треугольникам различной формы.

Вообще, оптимизация режимов работы электропривода должна производиться на основе технико-экономического критерия, в котором должны учитываться массогабаритные и стоимостные показатели электропривода, суммарные потери в электродвигателе и преобразователе частоты, потребление реактивной мощности от питающей сети. Но вследствие неоднозначности возможных режимов электропривода, недостаточности исходной информации приходится отказываться от реализации строго оптимальных режимов, а отдавать предпочтение режимам более простым. Причем, последние по своим технико-экономическим показателям часто оказываются несущественно хуже оптимальных.

В синхронных частотно-регулируемых электроприводах требования оптимального использования габаритной мощности СД (и установленной мощности НПЧ) приводят к необходимости выполнения следующих условий:

- обеспечение работы СД с номинальным потокосцеплением статора во всем диапазоне изменения нагрузок и регулирования скорости (за исключением режима ослабления поля при двухзонном регулировании);

- обеспечение работы СД с коэффициентом мощности, равным или близким единице.

На векторной диаграмме первое условие означает выполнение неравенства

Ф < Фн,

где Фн – величина номинального потока электродвигателя.

Этим условием исключается режим насыщения магнитной системы электродвигателя.

Коэффициент мощности на зажимах статора электродвигателя равен единице, если угол j между векторами Iс и Uc равен нулю. Это будет выполняться, если угол между векторам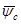и и прямой.

В зависимости от конкретных условий можно принять и обосновать другие законы возможного управления электромагнитными координатами электродвигателя, которым соответствуют иные требования к форме его векторной диаграммы.

Исходя из сказанного, можно сформулировать второе правило векторного регулирования электромагнитного момента: чтобы при регулировании момента электродвигателя добиться оптимальных режимов работы электропривода, необходимо в соответствии с выбранными критериями оптимизации соблюдать (с помощью системы регулирования) определенную форму моментного треугольника этого электродвигателя.

Date: 2015-07-02; view: 1055; Нарушение авторских прав