
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Основные формулы и обозначения. Длина гармонической волны связана с периодом и фазовой скоростью соотношением:
|
|
Длина гармонической волны 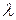 связана с периодом
связана с периодом 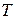 и фазовой скоростью
и фазовой скоростью 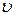 соотношением:
соотношением:  . Волновое число (модуль волнового вектора
. Волновое число (модуль волнового вектора 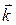 ,
, 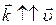 ):
): 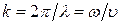 , где
, где 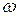 – круговая частота.
– круговая частота.
Уравнение бегущей волны имеет вид: 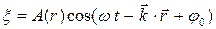 , где
, где 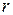 – расстояние от источника волны до колеблющейся точки;
– расстояние от источника волны до колеблющейся точки; 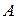 – амплитуда;
– амплитуда; 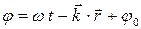 – фаза волны.
– фаза волны.
При расчетах обычно важна не фаза, а разность фаз. Разность фаз в двух точках на расстояниях 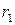 и
и 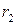
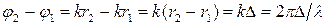 , (17)
, (17)
где 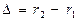 – разность хода лучей.
– разность хода лучей.
 Уравнение плоской бегущей вдоль оси
Уравнение плоской бегущей вдоль оси  волны:
волны:
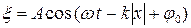 . (18)
. (18)
Максимальная скорость рас-пространения электромагнитных волн (ЭМВ) – их скорость в вакууме, равная скорости света в вакууме 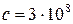 м/с. Скорость распростра-нения ЭМВ в среде
м/с. Скорость распростра-нения ЭМВ в среде 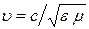 , где
, где 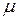 и
и 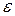 – соответственно магнитная и диэлектрическая проницаемости среды. Плоские ЭМВ (рис. 4) в нейтральной непроводящей среде являются поперечными: направления колебаний векторов напряженности электрического и магнитного полей перпендикулярны направлению распространения волны:
– соответственно магнитная и диэлектрическая проницаемости среды. Плоские ЭМВ (рис. 4) в нейтральной непроводящей среде являются поперечными: направления колебаний векторов напряженности электрического и магнитного полей перпендикулярны направлению распространения волны: 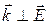 и
и 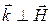 . Векторы напряженности электрического и магнитного полей плоской ЭМВ в любой момент времени взаимно перпендикулярны:
. Векторы напряженности электрического и магнитного полей плоской ЭМВ в любой момент времени взаимно перпендикулярны: 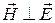 . Частоты колебаний напряженности электрического и магнитного полей плоской ЭМВ, и их фазы одинаковы в любой момент времени. Проекции напряженностей электрического и магнитного полей плоской ЭМВ и амплитуды их колебаний связаны между собой соотношениями
. Частоты колебаний напряженности электрического и магнитного полей плоской ЭМВ, и их фазы одинаковы в любой момент времени. Проекции напряженностей электрического и магнитного полей плоской ЭМВ и амплитуды их колебаний связаны между собой соотношениями 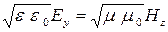 и
и 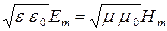 соответственно.
соответственно.
Уравнения колебаний векторов 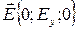 и
и 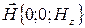 в плоской волне, распространяющейся вдоль оси
в плоской волне, распространяющейся вдоль оси  на расстоянии
на расстоянии 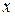 от начала отсчета, имеют вид:
от начала отсчета, имеют вид:  ;
; 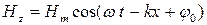 .
.
Задачи
120 (2). В упругой среде вдоль оси  распространяется плоская волна от источника, совершающего гармонические колебания с амплитудой 5 см и периодом колебаний 2 с. Скорость распространения волны 15 м/с. Найти: 1) циклическую частоту колебаний; 2) волновое число; 3) расстояние между двумя точками, лежащими на одном луче, для которых разность фаз колебаний равна
распространяется плоская волна от источника, совершающего гармонические колебания с амплитудой 5 см и периодом колебаний 2 с. Скорость распространения волны 15 м/с. Найти: 1) циклическую частоту колебаний; 2) волновое число; 3) расстояние между двумя точками, лежащими на одном луче, для которых разность фаз колебаний равна 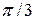 ; 4) скорость и ускорение, с которыми колеблются частицы среды в тот момент, когда смещение источника колебаний от положения равновесия минимально.
; 4) скорость и ускорение, с которыми колеблются частицы среды в тот момент, когда смещение источника колебаний от положения равновесия минимально.
121 (2). Плоская упругая волна распространяется вдоль оси  от источника колебаний, которые совершаются по закону:
от источника колебаний, которые совершаются по закону: 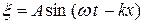 , где
, где 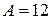 см;
см; 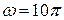 с-1;
с-1; 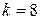 см-1,
см-1, 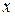 – расстояние от источника. Найти: 1) длину этой волны; 2) скорость распространения волны; 3) фазу волны в точке, находящейся на расстоянии 15 м от источника в тот момент, когда смещение источника от положения равновесия равно нулю; 4) ускорение этой точки в указанный момент времени; 5) скорость точки, расположенной на расстоянии 2 м от источника спустя половину периода от начала колебаний.
– расстояние от источника. Найти: 1) длину этой волны; 2) скорость распространения волны; 3) фазу волны в точке, находящейся на расстоянии 15 м от источника в тот момент, когда смещение источника от положения равновесия равно нулю; 4) ускорение этой точки в указанный момент времени; 5) скорость точки, расположенной на расстоянии 2 м от источника спустя половину периода от начала колебаний.
122 (2). Плоская гармоническая волна с периодом 0,1 с и амплитудой 12 см распространяется со скоростью 14 м/с в упругой среде. Найти: 1) длину волны; 2) волновое число; 3) разность фаз колебаний для точек, лежащих на одном луче на расстоянии 28 м друг от друга; 4) смещение точки, находящейся на расстоянии 42 м от источника волны спустя 20 с от начала колебаний источника. Уравнение колебаний источника имеет вид: 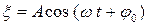 . В начальный момент времени скорость колебаний источника имела максимальное положительное значение.
. В начальный момент времени скорость колебаний источника имела максимальное положительное значение.
123 (2). Упругая плоская гармоническая волна распространяется вдоль оси  от источника, совершающего колебания с периодом 0,5 с и амплитудой 15 см. До точки
от источника, совершающего колебания с периодом 0,5 с и амплитудой 15 см. До точки 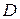 , расположенной на расстоянии 40 м от источника, волна доходит за 2 с. Найти: 1) длину волны; 2) скорость распространения волны; 3) разность фаз колебаний двух точек источника и точки
, расположенной на расстоянии 40 м от источника, волна доходит за 2 с. Найти: 1) длину волны; 2) скорость распространения волны; 3) разность фаз колебаний двух точек источника и точки 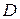 ; 4) скорость колебаний в указанной точке в тот момент, когда смещение источника от положения равновесия максимально; 5) ускорение колебаний в этой точке спустя 3/4 периода от начала колебаний источника. Начальную фазу принять равной нулю.
; 4) скорость колебаний в указанной точке в тот момент, когда смещение источника от положения равновесия максимально; 5) ускорение колебаний в этой точке спустя 3/4 периода от начала колебаний источника. Начальную фазу принять равной нулю.
124 (2). В упругой среде вдоль оси  распространяется плоская волна, уравнений которой имеет вид:
распространяется плоская волна, уравнений которой имеет вид: 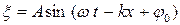 , где
, где 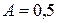 см;
см; 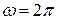 с-1;
с-1; 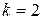 м-1,
м-1, 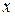 – расстояние от источника. В начальный момент времени смещение источника колебаний от положения равновесия равно 0,5 см. Найти: 1) частоту колебаний частиц среды, в которой распространяется волна; 2) скорость распространения волны; 3) длину волны; 4) ускорение колебаний частиц, расположенных на расстоянии 5 м от источника спустя 10 с от начала колебаний; 5) разность фаз колебаний двух частиц, лежащих на одном луче на расстоянии 314 м друг от друга.
– расстояние от источника. В начальный момент времени смещение источника колебаний от положения равновесия равно 0,5 см. Найти: 1) частоту колебаний частиц среды, в которой распространяется волна; 2) скорость распространения волны; 3) длину волны; 4) ускорение колебаний частиц, расположенных на расстоянии 5 м от источника спустя 10 с от начала колебаний; 5) разность фаз колебаний двух частиц, лежащих на одном луче на расстоянии 314 м друг от друга.
125 (2). В упругой среде вдоль оси  распространяется плоская гармоническая волна от источника, совершающего колебания по закону:
распространяется плоская гармоническая волна от источника, совершающего колебания по закону: 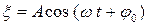 , где
, где 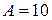 см;
см; 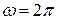 с-1. Скорость распространения волны 20 м/с. В начальный момент времени ускорение источника колебаний имело максимальное отрицательно значение. Найти: 1) волновое число; 2) длину волны; 3) скорость колебаний частиц, расположенных на расстоянии 50 м от источника спустя 15 с от начала колебаний; 5) разность фаз колебаний в двух точках, лежащих на одном луче, до которых волна доходит соответственно через 10 и 15 c от начала колебаний источника.
с-1. Скорость распространения волны 20 м/с. В начальный момент времени ускорение источника колебаний имело максимальное отрицательно значение. Найти: 1) волновое число; 2) длину волны; 3) скорость колебаний частиц, расположенных на расстоянии 50 м от источника спустя 15 с от начала колебаний; 5) разность фаз колебаний в двух точках, лежащих на одном луче, до которых волна доходит соответственно через 10 и 15 c от начала колебаний источника.
126 (2). Плоская электромагнитная волна распространяется вдоль оси  а) в вакууме, б) в однородной изотропной непроводящей немагнитной среде с диэлектрической проницаемостью, равной 2. Период колебаний вектора напряженности магнитного поля – 5·10-12 с, амплитуда – 1,7 мкА/м. Найти для обоих случаев: 1) скорость распространения волны; 2) значение напряженности электрического и магнитного полей в момент времени, равный 1/4 периода, в точке, расположенной на расстоянии 5 м от источника волн. Начальную фазу принять равной нулю.
а) в вакууме, б) в однородной изотропной непроводящей немагнитной среде с диэлектрической проницаемостью, равной 2. Период колебаний вектора напряженности магнитного поля – 5·10-12 с, амплитуда – 1,7 мкА/м. Найти для обоих случаев: 1) скорость распространения волны; 2) значение напряженности электрического и магнитного полей в момент времени, равный 1/4 периода, в точке, расположенной на расстоянии 5 м от источника волн. Начальную фазу принять равной нулю.
127 (2). Плоская электромагнитная волна распространяется вдоль оси  в однородной изотропной непроводящей немагнитной среде с диэлектрической проницаемостью, равной 3. Частота колебаний вектора напряженности магнитного поля равна 1012 Гц, амплитуда колебаний этого вектора – 8·103 А/м. Найти: 1) скорость распространения волны; 2) длину волны в вакууме и в данной среде; 3) значение напряженности электрического и магнитного полей в точках, расположенных на расстоянии 2 м от источника, и в момент времени, равный 1/6 периода, если начальная фаза колебаний источника равна
в однородной изотропной непроводящей немагнитной среде с диэлектрической проницаемостью, равной 3. Частота колебаний вектора напряженности магнитного поля равна 1012 Гц, амплитуда колебаний этого вектора – 8·103 А/м. Найти: 1) скорость распространения волны; 2) длину волны в вакууме и в данной среде; 3) значение напряженности электрического и магнитного полей в точках, расположенных на расстоянии 2 м от источника, и в момент времени, равный 1/6 периода, если начальная фаза колебаний источника равна 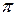 .
.
128 (2). Плоская монохроматическая электромагнитная волна распространяется в вакууме вдоль оси  . Частота колебаний вектора напряженности электрического поля – 4,5·1011 Гц. Найти: 1) длину волны в вакууме; 2) длину волны в однородной изотропной непроводящей немагнитной среде с диэлектрической проницаемостью, равной 3, и записать уравнение этой волны в указанной среде для вектора напряженности электрического поля, подставив численные значения всех входящих в уравнение величин. Амплитуда колебаний вектора напряженности магнитного поля в среде равна 5 мА/м. Начальную фазу принять равной нулю.
. Частота колебаний вектора напряженности электрического поля – 4,5·1011 Гц. Найти: 1) длину волны в вакууме; 2) длину волны в однородной изотропной непроводящей немагнитной среде с диэлектрической проницаемостью, равной 3, и записать уравнение этой волны в указанной среде для вектора напряженности электрического поля, подставив численные значения всех входящих в уравнение величин. Амплитуда колебаний вектора напряженности магнитного поля в среде равна 5 мА/м. Начальную фазу принять равной нулю.
129 (2). Плоская монохроматическая электромагнитная волна распространяется в вакууме вдоль оси  . Частота колебаний вектора напряженности электрического поля – 2·1011 Гц. Найти: длину волны и скорость распространения в однородной изотропной непроводящей немагнитной среде с диэлектрической проницаемостью, равной 4, и записать уравнение этой волны в указанной среде для вектора напряженности магнитного поля, подставив численные значения всех входящих в уравнение величин, если модуль вектора напряженности электрического поля в среде в начальный момент времени максимален и равен 10 В/м.
. Частота колебаний вектора напряженности электрического поля – 2·1011 Гц. Найти: длину волны и скорость распространения в однородной изотропной непроводящей немагнитной среде с диэлектрической проницаемостью, равной 4, и записать уравнение этой волны в указанной среде для вектора напряженности магнитного поля, подставив численные значения всех входящих в уравнение величин, если модуль вектора напряженности электрического поля в среде в начальный момент времени максимален и равен 10 В/м.
Date: 2015-06-11; view: 947; Нарушение авторских прав