Основные формулы и обозначения. С колебаниями и волнами встречаются при изучении самых разных физических явлений

ВВЕДЕНИЕ

С колебаниями и волнами встречаются при изучении самых разных физических явлений. Для понимания и решения задач на тему «Колебания и волны» требуются теоретические знания и навыки решения задач из других разделов физики. Поэтому, прежде чем приступить к решению задачи на данную тему, нужно тщательно изучить соответствующую теорию. Необходимые теоретические сведения имеются в литературе [1 – 7].

Несмотря на различную физическую природу, все колебательные процессы обладают общим характерным признаком – повторяемостью во времени – и исследуются с единой точки зрения. В частности, основным математическим аппаратом теории колебаний служат дифференциальные уравнения. Таким образом, одна из основных целей методических указаний – выработать общий подход к изучению всевозможных колебательных и волновых явлений.

Человек получает большую часть прямой информации об окружающем мире с помощью звуковых и световых волн, поэтому в физике особенно выделяют механические и электромагнитные колебания и волны.

Настоящие методические указания содержат большой набор разнообразных задач по теме «Колебания и волны». Пример правильного оформления решения задачи приведен в разд. 10.

Во всех задачах, включенных в методические указания, считается (если специально не оговорено в условии задачи), что колебания являются одномерными, т. е. состояние колеблющейся системы описывается зависимостью от времени только одной величины, которая называется обобщенной координатой.

После номера задачи в скобках указан уровень сложности (от 1 до 3).

ЧАСТОТА И ПЕРИОД СВОБОДНЫХ НЕЗАТУХАЮЩИХ КОЛЕБАНИЙ

Основные формулы и обозначения

Дифференциальное уравнение гармонических колебаний[1] имеет вид:

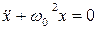, (1)

где 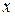– обобщенная координата системы, т. е. смещение системы от положения равновесия, меняющееся со временем по гармоническому закону;

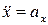– обобщенное ускорение;

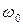– собственная (циклическая) частота колебаний системы.

Циклическая частота связана с частотой 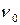и периодом 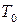собственных незатухающих колебаний соотношениями:

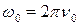; (2)

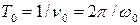. (3)

Возвращающая сила 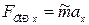, действующая на систему, совершающую свободные незатухающие колебания, подчиняется закону Гука:

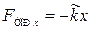, (4)

где 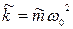– обобщенный коэффициент жесткости;

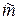– обобщенная масса.

Собственные частоты колебаний маятников:

1) 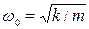– пружинного с массой 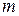и коэффициентом упругости пружины ;

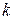2) 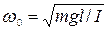– физического с массой 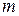, моментом инерции 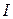и расстоянием 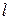от центра инерции до оси вращения ( 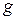– ускорение свободного падения);

3) 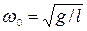– математического с нитью длиной .

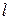Задачи

1 (1). Найти собственную частоту колебаний математического маятника длиной 94 см и массой 0,4 кг.

2 (1). Период гармонических колебаний пружинного маятника равен 1,4 с. Масса груза 215 г. Найти коэффициент упругости пружины.

3 (1). Золотое колечко, поставленное вертикально в небольшое углубление на горизонтальной плоскости, может совершать малые колебания вблизи положения устойчивого равновесия. Найти радиус колечка, если период колебаний равен 0,31 с.

4 (1). Однородный цилиндр радиусом 20 см подвешен на двух нитях равной длины к горизонтально закрепленной и расположенной на расстоянии 110 см от оси цилиндра перекладине. Найти период малых колебаний цилиндра вокруг перекладины (в вертикальной плоскости).

5 (1). Медный шарик, прикрепленный к пружине, совершает вертикальные колебания. Как изменится период колебаний, если к пружине подвесить вместо медного алюминиевый шарик такого же радиуса?

6 (1). Однородный стержень длиной 0,5 м совершает малые колебания в вертикальной плоскости около горизонтальной оси, проходящей 1) через его верхний конец; 2) через точку, находящуюся на расстоянии 0,1 м от верхнего конца. Найти период колебаний стержня.

7 (1). Однородный шарик подвешен на нити, длина которой равна радиусу шарика. Во сколько раз период малых колебаний этого маятника больше периода колебаний математического маятника с длиной, равной расстоянию от точки подвеса до центра тяжести шарика?

8 (2). К вертикально висящей пружине подвешен груз. При этом период колебаний равен 0,3 с. После того, как к первому грузу подвесили второй, период колебаний увеличился в 1,2 раза. На сколько удлинилась пружина после того, как к ней подвесили второй груз?

9 (2). Найти период малых вертикальных колебаний тела массой 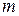, подвешенного на двух последовательно соединенных пружинках. Жесткости пружинок 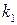и .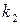

10 (3). Ареометр (прибор для измерения плотности жидкости в виде тонкого цилиндра диаметром 1 см) массой 0,2 кг плавает в жидкости. Если его немного погрузить в жидкость и отпустить, то он начнет совершать вертикальные колебания с периодом 3,4 с. Считая колебания незатухающими, определить из этих данных плотность жидкости, в которой плавает ареометр.

11 (3). Вычислить период свободных незатухающих колебаний цилиндрического поплавка на поверхности озера, если поплавку сообщили небольшой толчок в вертикальном направлении. Масса поплавка 20 г, его радиус 5 мм.

12 (3). Жидкость объемом 19 см³ налита в изогнутую U-образную трубку с одинаковой площадью сечения 0,5 см². Найти период малых колебаний жидкости. Трубка расположена вертикально.

13 (3). В кабине лифта подвешен математический маятник, период колебаний которого, когда лифт неподвижен, равен 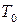. Каким будет период колебаний, если лифт станет опускаться с ускорением, равным 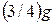? С каким ускорением нужно поднимать лифт, чтобы период колебаний маятника уменьшился вдвое?

14 (3). На каком расстоянии от центра нужно подвесить тонкий стержень длиной 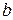, чтобы частота его колебаний была максимальна? Найти значение этой частоты.

Date: 2015-06-11; view: 670; Нарушение авторских прав