
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Основные формулы и обозначения. Пусть материальная точка совершает свободные незатухающие колебания с амплитудой вдоль оси вблизи начала координат
|
|
Пусть материальная точка совершает свободные незатухающие колебания с амплитудой 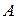 вдоль оси
вдоль оси  вблизи начала координат, совпадающего с положением устойчивого равновесия. Тогда координата точки, т. е. ее смещение от положения равновесия, меняется с течением времени
вблизи начала координат, совпадающего с положением устойчивого равновесия. Тогда координата точки, т. е. ее смещение от положения равновесия, меняется с течением времени 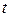 по гармоническому закону[2]:
по гармоническому закону[2]:
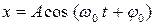 ,
, 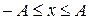 , (5)
, (5)
где 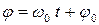 – фаза;
– фаза;
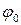 – начальная фаза колебаний.
– начальная фаза колебаний.
Проекции скорости 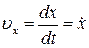 и ускорения
и ускорения 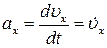 на ось
на ось  также меняются по гармоническому закону. Кроме того, координата и ускорение связаны между собой посредством уравнения (1), воспользовавшись которым можно решить обратную задачу, например, найти зависимость
также меняются по гармоническому закону. Кроме того, координата и ускорение связаны между собой посредством уравнения (1), воспользовавшись которым можно решить обратную задачу, например, найти зависимость 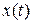 по известной зависимости
по известной зависимости 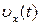 , или найти зависимость
, или найти зависимость 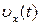 по известной зависимости
по известной зависимости 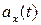 .
.
Потенциальная[3] и кинетическая энергия механических колебаний:
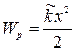 ;
; 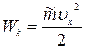 . (6)
. (6)
Полная энергия колебаний 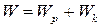 не зависит от времени:
не зависит от времени:
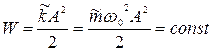 . (7)
. (7)
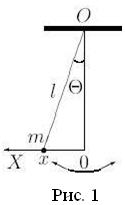
При колебаниях физического и математического маятников по гармоническому закону изменяются угол поворота 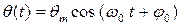 (
(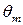 – амплитуда колебаний угла поворота), угловая скорость
– амплитуда колебаний угла поворота), угловая скорость 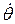 , угловое ускорение
, угловое ускорение 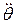 и т. д. (рис. 1).
и т. д. (рис. 1).
Кинетическая, потенциальная и полная энергия колебаний физического и математического маятников:
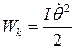 ;
; 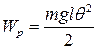 ;
;  .
.
Длина дуги окружности 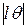 , описываемой грузом, при малых колебаниях математического маятника равна длине хорды и модулю горизонтального смещения груза
, описываемой грузом, при малых колебаниях математического маятника равна длине хорды и модулю горизонтального смещения груза 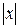 , поэтому
, поэтому 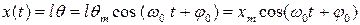 , где
, где 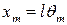 – амплитуда смещения вдоль горизонтальной оси.
– амплитуда смещения вдоль горизонтальной оси.
Задачи
15 (1). Материальная точка совершает гармонические колебания вдоль оси  по закону:
по закону: 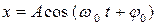 , где
, где 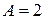 см;
см; 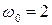 с-1;
с-1; 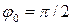 . Найти смещение точки от положения равновесия в момент времени, когда фаза равна 60°.
. Найти смещение точки от положения равновесия в момент времени, когда фаза равна 60°.
16 (1). Материальная точка совершает гармонические колебания вдоль оси  по закону:
по закону: 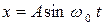 , где
, где 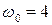 с-1. Найти амплитуду колебаний, если в момент времени, равный четверти периода, смещение точки было равно 4 см.
с-1. Найти амплитуду колебаний, если в момент времени, равный четверти периода, смещение точки было равно 4 см.
17 (1). Материальная точка совершает гармонические колебания вдоль оси  по закону:
по закону: 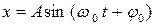 , где
, где 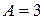 см;
см; 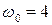 с-1. Найти начальную фазу колебаний, если в начальный момент времени смещение точки было равно 3 см.
с-1. Найти начальную фазу колебаний, если в начальный момент времени смещение точки было равно 3 см.
18 (1). Материальная точка совершает гармонические колебания вдоль оси  по закону:
по закону: 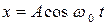 , где
, где 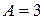 см;
см; 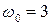 с-1. Найти проекцию скорости точки на ось
с-1. Найти проекцию скорости точки на ось  в момент времени, равный половине периода.
в момент времени, равный половине периода.
19 (1). Материальная точка совершает гармонические колебания вдоль оси  , при которых проекция ее скорости на эту ось меняется по закону:
, при которых проекция ее скорости на эту ось меняется по закону: 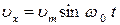 , где
, где 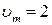 см/с;
см/с; 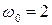 с-1. Найти проекцию ускорения точки на ось
с-1. Найти проекцию ускорения точки на ось  в момент времени, равный четверти периода.
в момент времени, равный четверти периода.
20 (1). Материальная точка совершает гармонические колебания вдоль оси  , при которых проекция ее скорости на эту ось меняется по закону:
, при которых проекция ее скорости на эту ось меняется по закону: 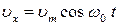 , где
, где 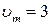 см/с;
см/с; 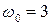 с-1. Найти координату точки в момент времени, равный половине периода.
с-1. Найти координату точки в момент времени, равный половине периода.
21 (1). Материальная точка совершает гармонические колебания вдоль оси  , при которых проекция ее ускорения на эту ось меняется по закону:
, при которых проекция ее ускорения на эту ось меняется по закону: 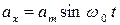 , где
, где 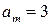 см/с;
см/с; 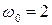 с-1. Найти проекцию скорости точки на ось
с-1. Найти проекцию скорости точки на ось  в момент времени, равный шестой части периода.
в момент времени, равный шестой части периода.
22 (2). Материальная точка массой 5 г совершает гармонические колебания вдоль оси  по закону:
по закону: 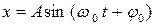 , где
, где 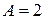 см;
см; 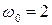 с-1. Найти: 1) начальную фазу колебания, если в начальный момент времени смещение точки от положения равновесия было равно 2 см; 2) ускорение точки в момент времени, равный четверти периода; 3) кинетическую и потенциальную энергию точки в момент времени, равный половине периода.
с-1. Найти: 1) начальную фазу колебания, если в начальный момент времени смещение точки от положения равновесия было равно 2 см; 2) ускорение точки в момент времени, равный четверти периода; 3) кинетическую и потенциальную энергию точки в момент времени, равный половине периода.
23 (2). Материальная точка массой 10 г совершает гармонические колебания вдоль оси  по закону:
по закону: 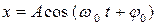 , где
, где 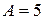 см;
см; 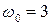 с-1. Найти: 1) начальную фазу колебания, если в начальный момент времени смещение точки от положения равновесия было равно 2,5 см; 2) скорость и ускорение точки в момент времени, когда смещение было минимальным; 3) максимальную силу и силу, действующую на точку в положении равновесия; 4) полную энергию точки.
с-1. Найти: 1) начальную фазу колебания, если в начальный момент времени смещение точки от положения равновесия было равно 2,5 см; 2) скорость и ускорение точки в момент времени, когда смещение было минимальным; 3) максимальную силу и силу, действующую на точку в положении равновесия; 4) полную энергию точки.
24 (2). Материальная точка совершает гармонические колебания вдоль оси  по закону:
по закону: 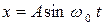 , где
, где 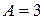 см;
см; 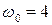 с-1. Найти фазу колебания и момент времени, ближайший к начальному, в который потенциальная энергия точки равна 200 мкДж, а проекция возвращающей силы - –2 мН.
с-1. Найти фазу колебания и момент времени, ближайший к начальному, в который потенциальная энергия точки равна 200 мкДж, а проекция возвращающей силы - –2 мН.
25 (2). Материальная точка совершает гармонические колебания вдоль оси  по закону:
по закону: 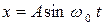 , где
, где 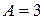 см;
см; 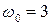 с-1. Найти фазу и момент времени, ближайший к началу колебаний, когда возвращающая сила имела значение 20 мН, а кинетическая энергия точки – 12 мкДж.
с-1. Найти фазу и момент времени, ближайший к началу колебаний, когда возвращающая сила имела значение 20 мН, а кинетическая энергия точки – 12 мкДж.
26 (2). Материальная точка массой 5 г совершает гармонические колебания вдоль оси  по закону:
по закону: 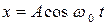 , где
, где 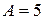 см;
см; 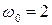 с-1. Определить проекции ускорения точки, и силы, действующей на точку, а также потенциальную энергию точки в момент времени, когда модуль ее скорости равен 8 см/с.
с-1. Определить проекции ускорения точки, и силы, действующей на точку, а также потенциальную энергию точки в момент времени, когда модуль ее скорости равен 8 см/с.
27 (2). Частица массой 3 г совершает гармонические колебания вдоль оси  по закону:
по закону: 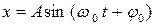 , где
, где 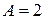 см;
см; 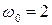 с-1. Найти модуль силы, действующей на частицу: 1) в тот момент, когда фаза колебаний равна 30°; 2) в точке наибольшего отклонения частицы от положения равновесия.
с-1. Найти модуль силы, действующей на частицу: 1) в тот момент, когда фаза колебаний равна 30°; 2) в точке наибольшего отклонения частицы от положения равновесия.
28 (2). Частица массой 10 г совершает гармонические колебания вдоль оси  . В некоторый момент времени смещение точки равно 5 см, проекция ее скорости равна 20 см/с, а проекция ускорения – -80 см/с2. Найти циклическую частоту, период и амплитуду колебаний, а также фазу в рассматриваемый момент времени.
. В некоторый момент времени смещение точки равно 5 см, проекция ее скорости равна 20 см/с, а проекция ускорения – -80 см/с2. Найти циклическую частоту, период и амплитуду колебаний, а также фазу в рассматриваемый момент времени.
29 (2). Найти циклическую частоту и амплитуду гармонических колебаний частицы вдоль оси  , если на расстояниях
, если на расстояниях 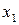 и
и 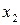 от положения равновесия проекция ее скорости равна соответственно
от положения равновесия проекция ее скорости равна соответственно 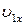 и
и 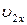 .
.
30 (2). Частица совершает колебания вдоль оси  по закону:
по закону: 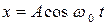 . В некоторый момент времени смещение точки от положения равновесия было равно 10 см. Когда фаза колебаний увеличилась вдвое, смещение стало равным 5 см. Найти амплитуду колебаний.
. В некоторый момент времени смещение точки от положения равновесия было равно 10 см. Когда фаза колебаний увеличилась вдвое, смещение стало равным 5 см. Найти амплитуду колебаний.
31 (2). Частица совершает колебания вдоль оси  по закону:
по закону: 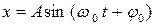 , где
, где 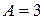 см;
см; 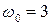 с-1. Найти: 1) фазу колебаний в момент времени, равный четверти периода, если в начальный момент времени смещение точки было равно 1,5 см; 2) момент времени, ближайший к началу колебаний, когда кинетическая энергия принимает максимальное значение, и число колебаний, которое точка совершила за это время.
с-1. Найти: 1) фазу колебаний в момент времени, равный четверти периода, если в начальный момент времени смещение точки было равно 1,5 см; 2) момент времени, ближайший к началу колебаний, когда кинетическая энергия принимает максимальное значение, и число колебаний, которое точка совершила за это время.
32 (2). Пружинный маятник совершает гармонические колебания вдоль оси  по закону:
по закону: 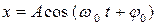 , где
, где 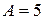 см;
см; 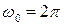 с-1;
с-1; 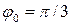 . Найти: 1) жесткость пружины маятника, если масса груза равна 1 кг; 2) момент времени, ближайший к началу колебаний, когда модуль ускорения маятника имеет максимальное значение; 3) полную энергию маятника.
. Найти: 1) жесткость пружины маятника, если масса груза равна 1 кг; 2) момент времени, ближайший к началу колебаний, когда модуль ускорения маятника имеет максимальное значение; 3) полную энергию маятника.
33 (2). Масса пружинного маятника – 0,5 кг, период собственных колебаний – 10 c. Пружину растянули на 10 см и отпустили. Найти: 1) начальную фазу колебаний; 2) модуль ускорения маятника спустя шестую часть периода от начала колебаний; 3) ближайший к началу колебаний момент времени, в который потенциальная энергия маятника будет максимальной.
34 (2). Стержень массой 1 кг и длиной 0,3 м укреплен так, что может вращаться относительно горизонтальной оси, проходящей через один из его концов. Сначала стержень висел вертикально. Затем его отклонили от положения равновесия на угол 10° и отпустили. Записать закон колебаний стержня. Найти: 1) период колебаний; 2) моменты времени, в которые кинетическая энергия стержня будет максимальной; 3) угловое ускорение маятника, его кинетическую и потенциальную энергию спустя одну треть периода колебаний.
35 (2). Математический маятник массой 3 кг, подвешенный на нити длиной 2 м, вывели из положения равновесия, сообщив грузу начальную скорость 20 см/с, направленную горизонтально вдоль оси  . По какому закону будет меняться угол отклонения маятника от положения равновесия? Найти значение потенциальной энергии маятника спустя шестую часть периода колебаний. В какой ближайший к началу колебаний момент времени проекция ускорения маятника на ось
. По какому закону будет меняться угол отклонения маятника от положения равновесия? Найти значение потенциальной энергии маятника спустя шестую часть периода колебаний. В какой ближайший к началу колебаний момент времени проекция ускорения маятника на ось  будет равна 0,3 м/с2?
будет равна 0,3 м/с2?
36 (2). Пружинный маятник совершает колебания вдоль оси  , при которых проекция его скорости на эту ось меняется по закону:
, при которых проекция его скорости на эту ось меняется по закону: 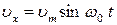 , где
, где 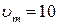 см/с;
см/с; 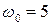 с-1. В какие моменты времени (считая от начала колебаний) проекция ускорения маятника будет иметь максимальное отрицательное значение? Найти потенциальную энергию маятника в момент времени, равный 1/8 периода после начала колебаний, если масса груза 2 кг.
с-1. В какие моменты времени (считая от начала колебаний) проекция ускорения маятника будет иметь максимальное отрицательное значение? Найти потенциальную энергию маятника в момент времени, равный 1/8 периода после начала колебаний, если масса груза 2 кг.
37 (2). Математический маятник массой 1 кг совершает колебания, при которых проекция его ускорения на ось  меняется по закону:
меняется по закону: 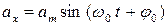 , где
, где 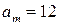 см/с2;
см/с2; 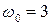 с-1. Найти: 1) длину нити маятника; 2) начальную фазу колебаний, если в начальный момент времени проекция ускорения была равна -12 см/с2; 3) кинетическую энергию маятника в момент времени, равный 1/12 периода колебаний; 4) возвращающую силу спустя половину периода от начала колебаний.
с-1. Найти: 1) длину нити маятника; 2) начальную фазу колебаний, если в начальный момент времени проекция ускорения была равна -12 см/с2; 3) кинетическую энергию маятника в момент времени, равный 1/12 периода колебаний; 4) возвращающую силу спустя половину периода от начала колебаний.
38 (3). К вертикально расположенной пружине подвесили два груза по 100 г каждый, в результате пружина растянулась на 5 см. Через некоторое время нижний груз упал. Определить смещение, скорость и ускорение оставшегося груза через 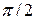 с. Ускорение свободного падения принять равным 10 м/с2.
с. Ускорение свободного падения принять равным 10 м/с2.
39 (3). На нити длиной 50 см висит маленький шарик массой 0,6 кг. В шар попадает пуля массой 20 г, летящая горизонтально со скоростью 7 м/с, и застревает в нем. Считая колебания системы гармоническими, записать закон колебаний. Найти: 1) период колебаний маятника; 2) момент времени (от начала колебаний), когда модуль скорости шарика будет равен 2 м/с; 3) максимальный угол, на который отклонится нить маятника от положения равновесия; 4) потенциальную энергию маятника спустя одну четверть периода колебаний.
40 (3). На горизонтальной плоскости покоился брусок массой 500 г, прикрепленный к пружине, второй конец которой надет на крючок, вбитый в стенку. Пружина не деформирована, ее жесткость 200 Н/м. Пуля массой 10 г, летевшая вдоль оси пружины в направлении стенки, попала в брусок и застряла в нем. В результате взаимодействия пружина сжалась на 8 см. Найти: 1) частоту колебаний системы; 2) значение модулей скорости и ускорения, а также значение потенциальной энергии системы в момент времени, равный трети периода, после начала колебаний; 3) модуль скорости пули до удара. Трением между бруском и плоскостью пренебречь.
41 (3). Математический маятник массой 1 кг совершает гармонические колебания с частотой 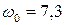 с-1. Эти колебания возникли после того, как, отклонив нить от положения равновесия на угол 2,5°, сообщили грузу начальную угловую скорость 6 рад/с. Начальная угловая скорость была направлена так, что маятник начал движение к положению равновесия. Найти: 1) длину нити; 2) начальную фазу и амплитуду колебаний; 3) модуль и направление возвращающей силы спустя четверть периода; 4) потенциальную энергию спустя 1/8 периода.
с-1. Эти колебания возникли после того, как, отклонив нить от положения равновесия на угол 2,5°, сообщили грузу начальную угловую скорость 6 рад/с. Начальная угловая скорость была направлена так, что маятник начал движение к положению равновесия. Найти: 1) длину нити; 2) начальную фазу и амплитуду колебаний; 3) модуль и направление возвращающей силы спустя четверть периода; 4) потенциальную энергию спустя 1/8 периода.
Date: 2015-06-11; view: 1037; Нарушение авторских прав