Оценка алгоритма

Оценка алгоритма бывает нужной в том случае, когда при решении некоторой задачи есть несколько разных алгоритмов, и стоит задача выбора одного из них для реализации. Даже если задача решается единственным алгоритмом, бывает нужно оценить сложность его реализации и его работы (объём памяти, время решения).

Под пространственной эффективностью понимают объём памяти, требуемой для выполнения программы.

Временная эффективность программы определяется временем, необходимым для ее выполнения. При этом необходимо учитывать следующие моменты.

Во-первых, время работы программы может ограничиваться ее назначением. Если эта программа реального времени, например, бронирования авиабилетов, то время обработки задания не должно превышать нескольких минут. Если эта программа автоматического управления каким-либо устройством (например, управлением самолёта), то она должна «успевать» отрабатывать поступающую информацию и своевременно выдавать управляющие воздействия.

Во-вторых, бывает важно знать, как изменяется время работы программы при увеличении размерности задачи. Это позволит оценить объем исходных данных, которые могут быть обработаны на компьютере за приемлемое время.

Реальное время работы программы на компьютере зависит не только от выбранного алгоритма. В значительной степени оно определяется типом ЭВМ, структурой представления данных, программной реализацией.

Самым простым способом оценить алгоритм – сопоставить ему число элементарных операций в описании. При реализации это может быть число команд в программе или объём памяти, которую занимает программа. В этом случае оценка d алгоритма A есть некоторое число k: d(A) = k.

Более интересной может быть оценка пары: алгоритма A и конкретной задачи a, которая им решается. Например, оценкой может быть объем памяти под программу, исходные и промежуточные данные, необходимые для решения данной задачи a, или время для решения данной задачи с помощью алгоритма A. В любом случае это будет число d(A(a)) = k(a).

Свойство массовости алгоритма предполагает, что алгоритм будет использоваться для решения класса A подобных задач, с разными исходными данными. Поэтому более сложной оценкой будет оценка как функция свойства задачи. Cопоставим каждой задаче из класса задач, решаемым алгоритмом, некоторый вектор числовых параметров задачи N = (n1, n2, …, nt). В этом случае оценка d(A(A)) = k(N), и это уже будет функция от параметров задачи.

Пример. Необходимо ценить алгоритм Прима – алгоритм выделения минимального остова. В первом случае мы рассматриваем число операторов в описании программы, реализующий алгоритм – число сравнений, условных переходов и т.д. Во втором случае анализируется работа алгоритма (программы) выделения остова некоторого заданного графа и определяется необходимый объём памяти. В последнем случае графу припишем параметры – число вершин в графе и число его рёбер, и сопоставим решению задачи функцию от этих параметров.

Во многих задачах возможно свести вектор задачи к одному параметру. Так, для графа возможно характеризовать его числом вершин, учитывая, что число ребер в нём коррелированно с числом вершин. Для задач, связанных с булевыми функциями, параметром может быть число аргументов функции.

Будем рассматривать только такие задачи. В этом случае оценкой алгоритма будет функция от одного параметра. Временная сложность алгоритма отражает требующиеся для его работы затраты времени Эта функция вставит каждой входной длине n в соответствие максимальное (по всем индивидуальным задачам длины n) время, затрачиваемое алгоритмом на решение индивидуальных задач этой длины.

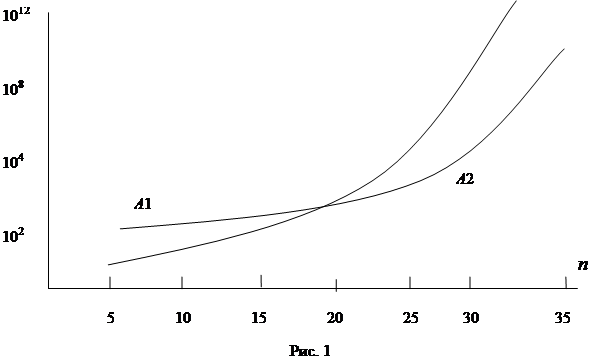
Пример. Пусть функция оценки имеет вид как на рис.1. Необходимо решать задачи с параметром n, лежащим в пределах от 5 до 15. В этом случае необходимо выбрать для реализации алгоритм A1. Если параметр меняется от 20 до 30, лучше использовать алгоритм A2. Если параметр меняется в пределах от 10 до 35, то возможно или выбрать любой из данных алгоритмов, или построить новый алгоритм, который, например, проверяет каждый раз значение параметра и выбирает соответствующий алгоритм.

Предположим, что можно рассмотреть все возможные алгоритмы A_i решения задачи a и для каждого параметра n оценить задачу двумя оценками d₁(a) = min (d(A_i (a))) и d₂(a) = max (d(A_i (a))), где min и max берётся по всем алгоритмам. В этом случае получим две границы решения данной задачи – нижнюю и верхнюю (рис.2). Этот рисунок определяет тот разброс сложности решений задачи и помогает ответить на вопрос: нужно ли тратить силы на поиск хорошего алгоритма или достаточно взять первый попавшийся.

Очень часто возможно оценить исходя из анализа самой задачи вид функции оценки с точностью до некоторого сомножителя – константы. В этом случае эта оценка будет не только оценка алгоритма, но и оценка задачи.

Функция f (n)есть O(g(n)), если существует константа с, такая, что f (n)< O(g(n)) для всех значений n>0.

По виду этой функции алгоритмы разделяются на следующие группы:

с линейной оценкой сложности, если функция d=C·n;

с квадратичной сложностью, если d = C · n²;

с полиномиальной сложностью, если d = C0 + C1·n +…+ Ck · n^k;

с факториальной сложностью, если d=C·n!;

с экспоненциальной сложностью, если d = C · a ⁿ;

с гиперэкспоненциальной сложностью, если d = C · a ^t, где t = a ⁿ.

Здесь C, a и k = некоторые константы, при этом число C может быть очень большим.

Date: 2015-07-01; view: 656; Нарушение авторских прав