
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Машина Тьюринга
|
|
Одно из уточнений понятий алгоритма было дано Э. Постом и А. Тьюрингом независимо друг от друга в 1936-1937гг. Основная мысль их заключалась в том, что алгоритмические процессы – это процессы, которые может свершить подходящим образом устроенная ”машина”. Ими были описаны гипотетические (условные) устройства, которые получили название «Машина Поста» и «Машина Тьюринга»(МТ). Так как в них много общего, то рассмотрим только машину Тьюринга.
Машина Тьюринга состоит из следующих частей:
1. Информационной ленты, представляющей бесконечную память машины. Это бесконечная лента, разделенная на ячейки. В каждой ячейке можно поместить лишь один символ из возможного их множества S={S1,S2,….,Sm},которое составляет внешний алфавит МТ. В этом алфавите один из символов (пусть это будет S1) соответствует пустому символу.
2. Считывающей головки – чувствительного специального элемента, способного обозревать содержимое ячеек. Лента может перемещаться вдоль головки так, что в каждый момент времени головка обозревает одну ячейку.
3. Управляющего устройства (УУ), которое в каждый момент времени находится в некотором состоянии. Число состояний конечно. Обозначим множество состояний как {q1,q2,…,qn}. Среди состояний одно соответствует заключительному, при котором МТ останавливается. УУ связано со считывающей головкой.
Кроме того, УУ вырабатывает три команды на перемещение ленты: П, Л, Н, где
П – переместиться на соседнюю справа ячейку;
Л – переместиться соседнюю слева ячейку;
Н – продолжать обозревать ту же ячейку.
Совокупность символов {q1,q2,…,qn} и {П,Л,Н} образуют внутренний алфавит МТ.
Работа машины происходит в дискретном времени. В начальный момент времени в ограниченный участок ленты записано слово в алфавите S, представляющее исходное условие задачи. В остальных ячейках предполагается записанным пустой символ. Управляющее устройство находится в начальном состоянии q1. На каждом шаге работы МТ обозревает на ленте символ Sk и в зависимости от него и от состояния qi, переходит в состояние qj, заменяет Sk на символ Sl и передвигает ленту (либо нет) на одну ячейку.
Каждая элементарная операция имеет вид
qiSk ® qjSl П(Л,Н).
Множество элементарных операций упорядочено и образует абстрактную программу, которая представляет алгоритм.
Считывающая головка и управляющее устройство образуют логический блок, который представляет собой (2,3)-полюсник.
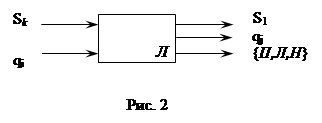
Структура МТ имеет следующий вид:
| S1 | S2 | … | Sk | … | Sm |
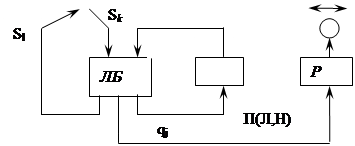
Q - ячейка хранит символ состояния, а Р - ячейка – символ сдвига. В них происходит задержка данных символов до начала следующего такта.
В качестве начальной информации на ленту можно записать любую конечную последовательность символов (входное слово) U внешнего алфавита. В начале работы алгоритма устройство управления находится в начальном состоянии, головка обозревает первый слева непустой символ входного слова U. Если после конечного числа тактов МТ останавливается, переходя в заключительное состояние, а на ленте оказывается информация B, то говорят, что машина применима к последовательности U и перерабатывает ее в последовательность B.
Если остановка и сигнал об остановке никогда не поступают, то говорят, что МТ не применима к последовательности U.
Рассмотрим функционирование МТ на примере сложения двух чисел, которые будем изображать в виде набора единиц.
Внешний алфавит будет состоять из символов: {1, +, Ù}, где Ù – пустой символ.
Внутренний алфавит будет состоять из четырех символов {q1, q2, q3,!}, где символ q1 означает начальное состояние, а! – заключительное состояние.
Пусть на ленте записана начальная информация:
| + |
МТ должна ее переработать в результирующую информацию:
Абстрактная программа, реализующий операцию сложения, будет иметь вид:
1q1  →Ùq3П
1q3→1q3П
+q3→+q3П →Ùq3П
1q3→1q3П
+q3→+q3П
| Ùq3→1q2H +q2 →+q2Л 1q2→1q2Л Ùq2 →Ùq1П +q1 →Ù!Н |
Начальное состояние УУ=q1, состояние ленты имеет вид:
| + |

 После первого шага состояние YY=q3, состояние ленты как на рис.
После первого шага состояние YY=q3, состояние ленты как на рис.
| + |
| + |
После пятого шага YY перейдёт в состояние q2. Состояние ленты показано на рис.
После десятого шага YY в состоянии q1 (рис.)
 1 1
| + |
Последовательность команд, реализующих операцию сложения, удобно задать таблицей, которую называют функциональной схемой алгоритма.
| q1 | q2 | q3 | |
| Ùq3П | 1q2Л | 1q3П | |
| Ù | Ùq1П | Ùq1П | 1q2H |
| + | Ù!Н | +q2Л | +q3П |
Основная гипотеза теории алгоритмов (тезис Чёрча)
Всякий алгоритм может быть задан посредством тьюринговой функциональной схемы и реализован в соответствующей машине Тьюринга.
Обоснование гипотезы.
Речь не идет о доказательстве гипотезы, так как она содержит не формализованные математические понятия.
Уверенность в справедливости гипотезы основана, главным образом, на опыте. Все известные к настоящему времени алгоритмы могут быть заданы посредством тьюринговых функциональных схем. Кроме того, внутри самой теории алгоритмов основная гипотеза не применяется, то есть при доказательстве теорем этой теории ссылок на основную гипотезу не делается.
Машина Тьюринга крайне примитивна. Но примитивность ее не в том, что она использует ленту и механическое движение головки, а то, что ее набор операций с памятью очень прост (запись и чтение символов) и что доступ к памяти в ней происходит не по адресу, а путем последовательного перемещения вдоль ленты. Поэтому выполнение на ней даже таких простых функций как сложение и умножение требует много шагов. Машина Тьюринга была придумана не для того, чтобы производить на ней реальные вычисления, а чтобы показать, что сколь угодно сложный алгоритм можно построить из очень простых операций, причем сами операции и переход от одной операции к другой выполняются автоматически.
Date: 2015-07-01; view: 830; Нарушение авторских прав