
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Плоские электромагнитные волны и их свойства
|
|
Рассмотрим однородную непроводящую (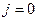 ) нейтральную (
) нейтральную ( ) безграничную среду, в которой распространяются электромагнитные возмущения.
) безграничную среду, в которой распространяются электромагнитные возмущения.
Четыре уравнения Максвелла с учетом двух материальных уравнений (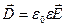 ,
, 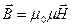 ) сводятся к следующим уравнениям для Е и Н:
) сводятся к следующим уравнениям для Е и Н:
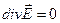 (1)
(1)
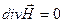 (2)
(2)
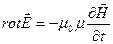 (3)
(3)
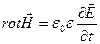 (4)
(4)
Ограничимся случаем, когда возмущение распространяется вдоль оси Х и напряженности Е и Н зависят только от х и t. Такое возмущение является плоской волной.
Перепишем уравнения (1) - (4) в координатной форме. Напомним, что
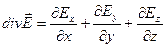 ,
, 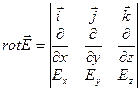 .
.
Из (1) и (2) получаем:
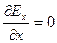 (1а),
(1а), 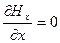 (2а).
(2а).
(3) и (4) – векторные уравнения. Каждое из них дает три уравнения для проекций на оси X, Y, Z:
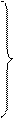
 (3- Х)
(3- Х) 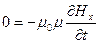 (4- X)
(4- X) 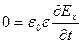
(3- Y) 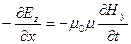 (4- Y)
(4- Y) 
(3- Z) 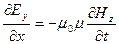 (4- Z)
(4- Z) 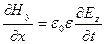
Из (1а) и (4- Х) мы делаем вывод, что Ех не зависит ни от х, ни от t, т.е. является однородным полем. Аналогично Нх. Однородные статичные поля не связаны с распространением возмущения, и их можно не учитывать.
Оставшиеся четыре уравнения распадаются на две независимые группы:
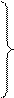 | 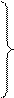 |
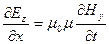
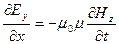
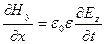 и
и 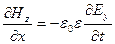
 Первая пара уравнений связывает друг с другом компоненты полей
Первая пара уравнений связывает друг с другом компоненты полей 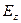 и
и 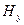 , вторая пара – поля
, вторая пара – поля 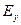 и
и 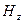 . Вывод: пара полей
. Вывод: пара полей 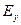 и
и 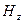 (или
(или 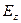 и
и 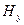 ) является взаимопорождающей, при этом другая пара полей не возникает:
) является взаимопорождающей, при этом другая пара полей не возникает: 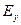 , меняясь со временем, порождает
, меняясь со временем, порождает 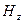 , и наоборот. В простейшем случае может существовать только
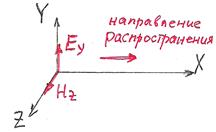
, и наоборот. В простейшем случае может существовать только  одна пара полей – например,
одна пара полей – например, 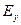 и
и 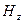 . Волна при этом, как оговорено с самого начала, распространяется вдоль оси Х.
. Волна при этом, как оговорено с самого начала, распространяется вдоль оси Х.
Вывод: электромагнитные волны поперечны:
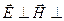 направлению распространения.
направлению распространения.
Выпишем еще раз уравнения для пары 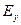 и
и 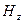 :
:
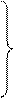 (5)
(5) 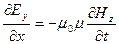

(6) 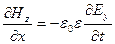
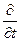
Продифференцируем первое уравнение по х, а второе – по t:
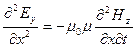 ,
,  .
.
Полученные уравнения содержат одну и ту же производную 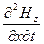 . Выразив ее из каждого уравнения и приравняв значения друг другу, приходим к уравнению:
. Выразив ее из каждого уравнения и приравняв значения друг другу, приходим к уравнению:
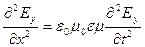 . (*)
. (*)
Точно такому же уравнению удовлетворяет и магнитное поле 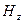 .
.
Сравним уравнение (*) с известным вам из курса Механики волновым уравнением, описывающим распространение возмущения (волны) со скоростью v:
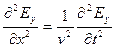 .
.
Вывод: скорость распространения электромагнитной волны  .
.
Скорость в вакууме (обозначим ее «с») равна 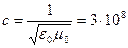 м/с.
м/с.
Скорость в среде  .
.
Решением волнового уравнения (*) являются любые функции вида 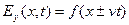 – плоские волны, бегущие в положительном направлении оси Х (при знаке «минус» в аргументе) или в отрицательном направлении (при знаке «плюс»).
– плоские волны, бегущие в положительном направлении оси Х (при знаке «минус» в аргументе) или в отрицательном направлении (при знаке «плюс»).
Такие же решения и для магнитного поля: 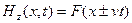 .
.
Найдем связь между мгновенными значениями Е и Н в волне.
Пусть волна бежит в положительном направлении оси Х:
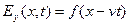 ,
, 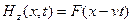 . (7)
. (7)
Уравнение (6) связывает производные 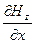 и
и 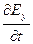 . Для волны (7)
. Для волны (7) 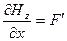 (штрихом мы обозначили производную от функции F по аргументу
(штрихом мы обозначили производную от функции F по аргументу 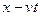 ),
), 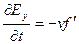 . Подставляем эти производные в (6) и получаем:
. Подставляем эти производные в (6) и получаем: 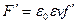 , откуда следует, что
, откуда следует, что 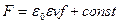 . Значение же константы можно принять равной нулю, т.к. постоянные поля нас не интересуют. Итак,
. Значение же константы можно принять равной нулю, т.к. постоянные поля нас не интересуют. Итак, 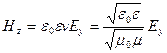 .
.
Сформулируем еще раз полученные выводы.
1) Электромагнитные волны являются поперечными: 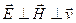
2) (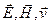 ) образуют правую тройку векторов.
) образуют правую тройку векторов.
3) Скорость волн в среде  , где
, где 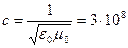 м/с – скорость в вакууме.
м/с – скорость в вакууме.
4) В каждый момент модули Е и Н (Е и В) пропорциональны друг другу:
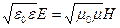 , или
, или 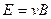
5) Плотности электрической ( ) и магнитной (
) и магнитной (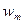 ) энергии в волне одинаковы:
) энергии в волне одинаковы:
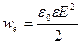 ,
, 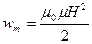 .
.
Полная плотность энергии
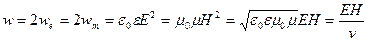 .
.
Хотя мы пришли к этим выводам на примере плоской волны, они остаются верными для всех типов электромагнитных волн.
Частным, но наиболее важным случаем плоской волны является плоская гармоническая волна с круговой частотой 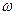 :
:
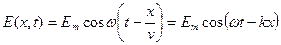 ,
,
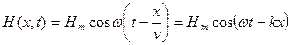 , где
, где 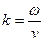 – волновое число.
– волновое число.
 Электрический и магнитный векторы в волне изменяются синфазно: одновременно (в каждой точке) достигают максимума и обращаются в ноль.
Электрический и магнитный векторы в волне изменяются синфазно: одновременно (в каждой точке) достигают максимума и обращаются в ноль.
Длина гармонической волны в вакууме
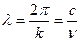
(где 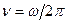 – частота колебаний в волне). В среде длина волны уменьшается в
– частота колебаний в волне). В среде длина волны уменьшается в 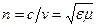 раз. Число
раз. Число 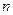 называют показателем преломления среды.
называют показателем преломления среды.
Date: 2015-06-11; view: 2300; Нарушение авторских прав