Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Полная система уравнений Максвелла
|
|
Полная система уравнений Максвелла для электромагнитного поля состоит из четырех интегральных (или дифференциальных) уравнений и двух так называемых материальных уравнений.
1) 
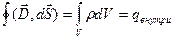– теорема Остроградского-Гаусса. Источниками электрического поля являются электрические заряды.
2) 
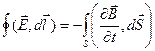–– переменное магнитное поле порождает вихревое электрическое поле.
3) 
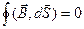– выражает отсутствие точек начала и конца («источников» и «стоков») линий магнитной индукции, вихревой характер магнитного поля.
4) 
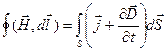– закон полного тока. Магнитное поле порождается как токами, так и переменным электрическим полем.
В дифференциальной форме:
.
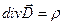
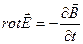
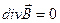
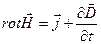В систему входят четыре вектора: два электрических (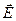
и 
) и 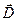два магнитных (
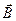и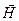 
).
В вакууме векторы каждой пары отличаются друг от друга только умножением на постоянную: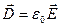 
, 
.
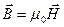В однородной изотропной среде связь векторов описывается двумя материальными уравнениями:
.
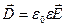
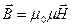Четыре уравнения Максвелла и два материальных уравнения образуют полную систему уравнений для нахождения электромагнитного поля по известному распределению сторонних зарядов и токов проводимости.
Date: 2015-06-11; view: 432; Нарушение авторских прав