Свойства уравнений Максвелла

1) Они линейные, т.е. содержат только первые производные полей по времени и координатам и первые степени j и 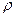. Из этого вытекает принцип суперпозиции.

2) Уравнения Максвелла являются релятивистскими: они выполняются во всех ИСО при любых скоростях движения зарядов (инвариантны относительно преобразований Лоренца). Вид уравнений при переходе из одной ИСО в другую не меняется. Но в разных ИСО разделение единого электромагнитного поля на электрическую и магнитную составляющие будет различным.

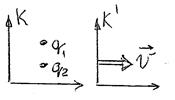Пример: в К -системе заряды покоятся, и существует только электрическое поле. В -системе заряды движутся, и существуют электрическое и магнитное поля.

3) Уравнения не симметричны относительно электрического и магнитного полей: это связано с существованием точечных электрических зарядов (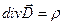) и отсутствием точечных «магнитных зарядов» ().

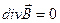Но в вакууме уравнения приобретают симметричный вид:

, ,

, .

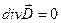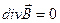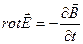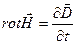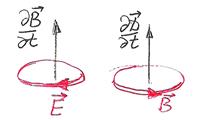
Левый винт Правый винт

Изменяющиеся со временем электрическое и магнитное поля взаимно порождают друг друга. Единственное отличие – в знаке производной.

4) Отсюда следует вывод о существовании нового физического явления:

Date: 2015-06-11; view: 507; Нарушение авторских прав