Краткие теоретические сведения. Амплитуда силы тока при вынужденных колебаниях в последовательном контуре зависит от внешней электродвижущей силы (ЭДС) Е и соотношения частоты возбуждения

Амплитуда силы тока при вынужденных колебаниях в последовательном контуре зависит от внешней электродвижущей силы (ЭДС) Е и соотношения частоты возбуждения (внешней вынуждающей силы) w и собственной w ₀ ([1, 2, 3]):

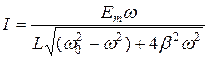, (11)

где Е_m – амплитудное значение ЭДС; L – индуктивность контура; β – коэффициент затухания (в электротехнических приложениях коэффициент затухания обозначается символом γ, в физике – β).

При резонансе (w = w ₀) амплитуда силы тока будет максимальной:

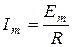, (12)

а сдвиг по фазе между силой тока в контуре и внешней ЭДС равен нулю. Если подать напряжение, пропорциональное силе тока в контуре, на горизонтально отклоняющие пластины осциллографа, а напряжение внешней ЭДС – на вертикально отклоняющие, то при значениях частоты внешней ЭДС, отличных от значения резонансной, на экране осциллографа будет наблюдаться фигура Лиссажу в виде эллипса. При совпадении частоты вынуждающей ЭДС с частотой собственных колебаний в контуре эллипс вырождается в отрезок. Это явление может быть использовано в качестве индикатора резонансных колебаний в контуре.

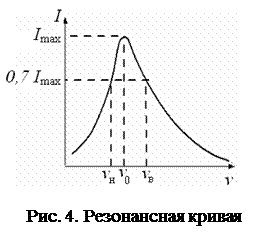График зависимости амплитуды вынужденных колебаний от частоты вынуждающей ЭДС (резонансная кривая) представлен на рис. 4, на котором показаны полосы пропускания контура (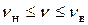) и графическое определение резонансной частоты n ₀. Частота n ₀ связана с добротностью контура формулой:

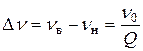, (13)

где ν _в, ν _н – нижняя и верхняя частоты полосы пропускания контура (в некоторых технических дисциплинах частота колебаний обозначается буквой f, в физике колебаний – символом ν); Q - добротность контура, Q связана с логарифмическим декрементом затухания соотношением:

. (14)

Date: 2015-06-11; view: 633; Нарушение авторских прав