
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Примеры решения задач. З а д а ч а 7. Идеальный колебательный контур состоит из конденсатора емкостью 200 мкФ и катушки индуктивностью 3 мГн
|
|
З а д а ч а 7. Идеальный колебательный контур состоит из конденсатора емкостью 200 мкФ и катушки индуктивностью 3 мГн. Конденсатор зарядили количеством электричества 70 мкКл и замкнули на катушку. Найти зависимости от времени энергии электрического и магнитного полей и построить графики этих зависимостей в пределах половины периода колебаний заряда.
Дано:
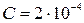 Ф; Ф;
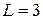 мГн; мГн;
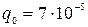 Кл.
Найти и построить графики: Кл.
Найти и построить графики: 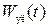 и и 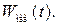
| Решение.
Энергия электрического и магнитного полей определяется по формулам:
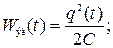 (53) (53)
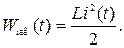 (54) (54)
|
где 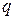 – заряд на пластинах конденсатора;
– заряд на пластинах конденсатора;
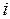 – сила тока, протекающего через катушку.
– сила тока, протекающего через катушку.
Так как контур идеальный, заряд совершает гармонические колебания:
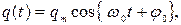 (55)
(55)
где
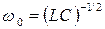 – (56)
– (56)
собственная частота колебаний в контуре;
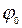 – начальная фаза, определяемая из закона (51) при
– начальная фаза, определяемая из закона (51) при 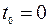 с:
с: 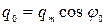 , откуда
, откуда
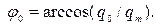 (57)
(57)
Согласно условию задачи в момент начала колебаний заряженный конденсатор замкнули на катушку, поэтому заряд на пластинах не может быть больше начального. Таким образом, амплитуда колебаний заряда равна начальному заряду:
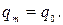 (58)
(58)
Подставив начальное условие (58) в формулу (57), получим:
 (59)
(59)
Таким образом, законы (55) и (53) колебаний заряда и энергии электрического поля в контуре с учетом равенства (56) принимают вид:
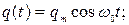 (60)
(60)
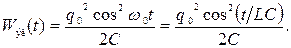 (61)
(61)
Закон колебаний силы тока найдем, взяв производную по времени от правой части формулы (60):
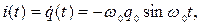 (62)
(62)
поэтому зависимость энергии магнитного поля от времени (50) с учетом равенства (56) принимает вид:
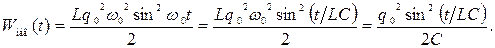 (63)
(63)
| Таблица 1 | ||
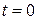
| 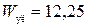 мкДж мкДж
| 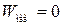 мкДж мкДж
|
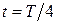
| 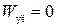 мкДж мкДж
| 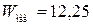 мкДж мкДж
|
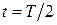
| 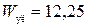 мкДж мкДж
| 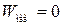 мкДж мкДж
|
Через полную энергию 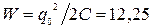 мкДж и период колебаний
мкДж и период колебаний 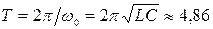 мс зависимости энергии от времени (61) и (63) представляются в виде:
мс зависимости энергии от времени (61) и (63) представляются в виде: 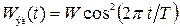 ;
; 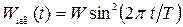 . Удобство этих формул заключается в значительном облегчении построения графиков и вычисления энергии при выборе значений времени
. Удобство этих формул заключается в значительном облегчении построения графиков и вычисления энергии при выборе значений времени 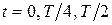 , отвечающих экстремумам гармонических функций. Построим графики. Значения энергии в выбранные моменты времени в пределах половины периода колебаний заряда показаны в табл. 1. Графики зависимости энергии от времени изображены на рис. 4.
, отвечающих экстремумам гармонических функций. Построим графики. Значения энергии в выбранные моменты времени в пределах половины периода колебаний заряда показаны в табл. 1. Графики зависимости энергии от времени изображены на рис. 4.
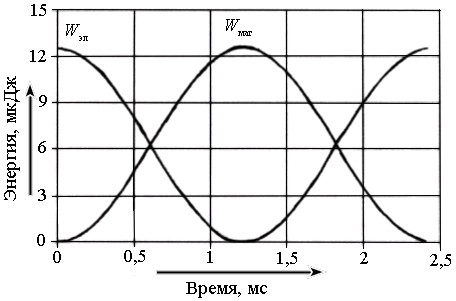
Рис. 4
Ответ: 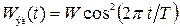 ,
, 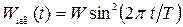 ,
,
где 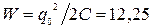 мкДж;
мкДж;
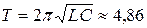 мс.
мс.
З а д а ч а 8. В идеальном колебательном контуре с емкостью 6 мкФ заряд на обкладках конденсатора меняется по закону: 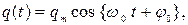 где
где 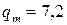 мкКл;
мкКл; 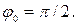 Найти разность потенциалов (напряжение) на обкладках конденсатора спустя четверть периода колебаний.
Найти разность потенциалов (напряжение) на обкладках конденсатора спустя четверть периода колебаний.
Дано:
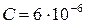 Ф; Ф;
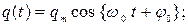 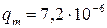 Кл; Кл;
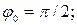
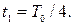 Найти:
Найти: 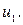
| Решение.
Напряжение связано с зарядом соотношением: 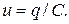 Подставляя в него закон колебаний заряда Подставляя в него закон колебаний заряда 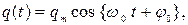 получим зависимость напряжения от времени: получим зависимость напряжения от времени:
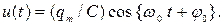 (64) (64)
|
Выразив в формуле (64) собственную частоту колебаний через период 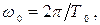 получим:
получим:
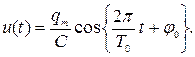 (65)
(65)
Подставив в формулу (65) численные данные при 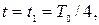 найдем:
найдем: 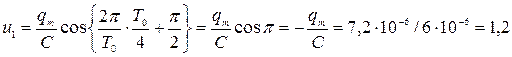 В.
В.
Ответ: 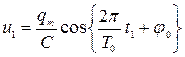 ,
, 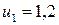 В.
В.
З а д а ч а 9. В идеальном колебательном контуре с индуктивностью 100 мГн совершаются гармонические колебания с частотой 400 Гц. Найти емкость конденсатора и закон изменения силы тока в контуре, если в начальный момент времени сила тока была максимальной и равной 16 мА.
Дано:
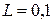 Гн; Гн;
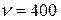 Гц; Гц;
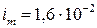 А; А;
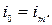 Найти:
Найти: 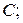 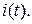
| Решение.
Закон колебаний силы тока в идеальном колебательном контуре имеет вид:
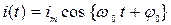 , (66)
где , (66)
где
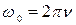 – (67) – (67)
|
собственная частота;
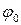 – начальная фаза колебаний, которая определяется из закона (66) при
– начальная фаза колебаний, которая определяется из закона (66) при 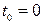 с в соответствии с начальным условием
с в соответствии с начальным условием 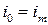 :
:
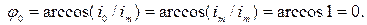 (68)
(68)
Подставив выражения (67) и (68) в закон (66), получим зависимость силы тока в рассматриваемом контуре от времени:
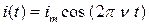 . (69)
. (69)
Емкость конденсатора найдем из выражения 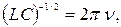 полученного подстановкой в соотношение (67) формулы
полученного подстановкой в соотношение (67) формулы 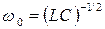 для собственной частоты колебаний в контуре:
для собственной частоты колебаний в контуре: 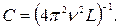 Отсюда
Отсюда 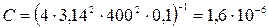 Ф.
Ф.
Ответ: 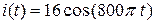 мА;
мА;
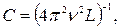
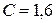 мкФ.
мкФ.
Date: 2015-06-11; view: 840; Нарушение авторских прав