
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Алгоритм идентификации параметров математической модели
|
|
Алгоритм идентификации, используемый в настоящей работе, основан на нестохастической (теоретико-множественной) интерпретации неопределенностей, присущих управляемому процессу или объекту. В данных алгоритмах /3/ неопределенным величинам не приписываются вероятностные свойства с указанием соответствующих статистических распределений. Указываются только некоторые гарантированные оценки множества их возможных значений.
Получение этих оценок основано на рассмотренных в /1/ идеях и способах аппроксимации выпуклых множеств специального вида (шаровых сегментах), содержащими их эллипсоидами.
Исходной информацией для работы алгоритма идентификации (АИ) являются уравнения (7) модели процесса /2/, текущие измерения вектора входов
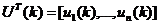
и выходов (показаний анализаторов, измеряющих октановое число смеси)
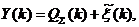 (10)
(10)
где  - ошибка измерений, причем известно, что
- ошибка измерений, причем известно, что
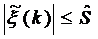 ,
,
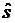 известная постоянная, определяемая классом точности измеряющего устройства.
известная постоянная, определяемая классом точности измеряющего устройства.
Предполагается известной также правая часть 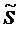 соотношения (8), определяющая меру несоответствия линейной модели
соотношения (8), определяющая меру несоответствия линейной модели
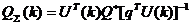
"истинной" модели процесса (7.1). Тогда, исходя из соотношений (7.1), (10) уравнение
измерения октанового числа может быть записано в виде
 , (11)
, (11)
где величина

характеризует как погрешность измерения, так и погрешность, вызванную тем, что формула (11) в целях упрощения ограничивается использованием только первого члена, входящим в уравнение (7.1) модели процесса.
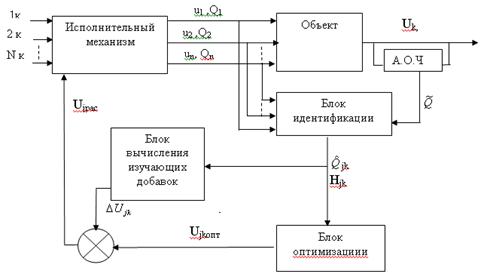
Схема адаптивной системы компаундирования товарных бензинов с модулем идентификации представлена на рис. 1.
Априорно известны оценки возможных значений компонент 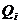 вектора Q коэффициентов модели (7) в виде интервалов (9), где
вектора Q коэффициентов модели (7) в виде интервалов (9), где 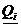 , и
, и 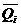 - заданные числа для всех i = 1,n. Величины
- заданные числа для всех i = 1,n. Величины 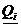 и
и 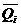 получаются из оценки результатов работы технологических процессов, предшествующих рассматриваемому, и задаются оператором-технологом.
получаются из оценки результатов работы технологических процессов, предшествующих рассматриваемому, и задаются оператором-технологом.
В результате работы алгоритма идентификации строится последовательность 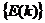 эллипсоидальных множеств в соответствующих пространствах
эллипсоидальных множеств в соответствующих пространствах 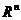 , данные множества в дальнейшем условимся называть просто эллипсоидами.
, данные множества в дальнейшем условимся называть просто эллипсоидами.
Эллипсоиды имеют вид:
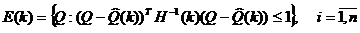 (12)
(12)
где 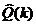 - центр эллипсоида,
- центр эллипсоида,
H(k)- симметрическая положительно определенная матрица, характеризующая многомерный объем эллипсоида.
При возрастании дискретного времени k многомерные объемы эллипсоидов E(k) монотонно убывают.
При этом гарантируется, что вектор Q* октановых чисел компонентов товарного бензина в смешиваемых потоках принадлежит эллипсоидам E(k), то есть, выполняются включения
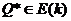 (13)
(13)
для всех k = 1,2,....
Центры 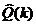 эллипсоидов принимаются за оценки вектора параметров Q*.
эллипсоидов принимаются за оценки вектора параметров Q*.
Описание алгоритма идентификации приведено в /3/.
Для описания алгоритма построения эллипсоида Е(0) по известному эллипсоиду
Е(k), k = 1, 2,..., введем следующие обозначения
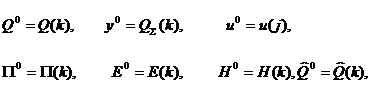 (14)
(14)
где индекс k дискретного времени для сокращения последующих записей опущен.
Построение эллипсоида E(k+1), то есть вычисление его параметров H(k+1) и 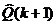 по известным H(k) и Q(k) осуществляется последовательно. На первом шаге строится эллипсоид E(k+1), покрывающий пересечение эллипсоида Е0 и полосы П0.
по известным H(k) и Q(k) осуществляется последовательно. На первом шаге строится эллипсоид E(k+1), покрывающий пересечение эллипсоида Е0 и полосы П0.
Затем строятся последовательно эллипсоиды Еj+1(k+1) = E j+1, покрывающие пересечения эллипсоидов Еj+1(k+1) с полосами П j. С учетом обозначений (14) алгоритм вычисления параметров H(k+1) и Q(k+1) эллипсоида E(k+1) может быть записан в следующем виде
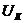 - объем продукта;
- объем продукта; 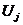 - объем j-го компонента;
- объем j-го компонента; 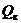 - октановое число продукта, (Yк);
- октановое число продукта, (Yк);
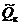 - показания О.Ч. на анализаторе октанового числа;
- показания О.Ч. на анализаторе октанового числа; 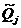 - октановое число j-го компонента;
- октановое число j-го компонента;
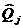 -индентиф-нное О.Ч. j-го компонента;
-индентиф-нное О.Ч. j-го компонента; 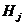 - симметрическая положительно опред-ная матрица;
- симметрическая положительно опред-ная матрица;
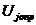 - оптимальный расход j-го компонента;
- оптимальный расход j-го компонента; 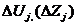 - изучающая добавка (поправка);
- изучающая добавка (поправка);
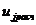 - расчетный расход j-го компонента; к - дискретное время;
- расчетный расход j-го компонента; к - дискретное время;
Рис. 1. Схема адаптивной системы компаундирования товарных бензинов.
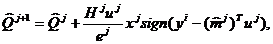
 (15)
(15)
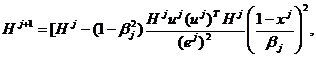 (16)
(16)
где
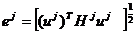 (17)
(17)
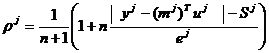 (18)
(18)
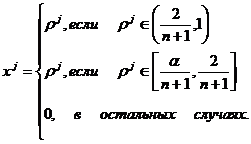 (19)
(19)
 (20)
(20)
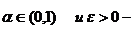 параметры алгоритма.
параметры алгоритма.
Если при этом получится, что
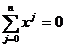 (21)
(21)
то полагается
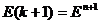 (22)
(22)
Если условие (21) не выполняется, то полагается
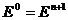 (23)
(23)
и весь цикл вычислений по формулам (15)-(21) повторяется. Эти циклы выполняются до тех пор, пока не выполнится условие (21) или же число этих циклов не станет равным некоторому целому числу L. В любом из этих случаев полагается 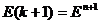 . Выбор максимального числа циклов L определяется временными ресурсами ЭВМ.
. Выбор максимального числа циклов L определяется временными ресурсами ЭВМ.
Если при построении эллипсоида 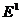 , покрывающего пересечение полосы
, покрывающего пересечение полосы 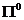 и эллипсоида
и эллипсоида 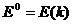 для его центра выполняется неравенство
для его центра выполняется неравенство
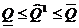 (24)
(24)
то вычисления по формулам (15)-(24) при j> 1 далее не производятся и полагается
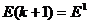 .
.
При нормальном функционировании анализаторов величина  удовлетворяет условию
удовлетворяет условию 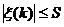 , где S - заданные числа /погрешность измерения октанового числа/. При возникновении неисправности /сбой анализатора/ может оказаться, что
, где S - заданные числа /погрешность измерения октанового числа/. При возникновении неисправности /сбой анализатора/ может оказаться, что  . Последнее означает, что некоторый эллипсоид
. Последнее означает, что некоторый эллипсоид 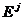 может не пересекаться с полосой
может не пересекаться с полосой 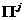 . В этом случае вычисленное значение параметра x j окажется больше единицы x j
. В этом случае вычисленное значение параметра x j окажется больше единицы x j 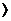 1. При этом полагается
1. При этом полагается 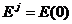 и процесс построения последующих эллипсоидов по формулам (15)-(24) продолжается по описанной выше схеме.
и процесс построения последующих эллипсоидов по формулам (15)-(24) продолжается по описанной выше схеме.
В соответствии с подходом к решению задачи оптимизации процесса компаундирования, сформулированным в разделе 1, задача линейного программирования (1)-(6) решается при условии, что вместо неизвестных октановых чисел 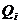 смешиваемых компонент берутся их оценки
смешиваемых компонент берутся их оценки 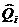 , получаемые с помощью алгоритма идентификации.
, получаемые с помощью алгоритма идентификации.
Очевидно, что решение задачи при оценках 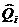 будет тем ближе к решению, при известных
будет тем ближе к решению, при известных 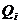 , чем точнее будут оценки
, чем точнее будут оценки 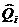 .
.
В результате получения уравнений измерения октанового числа (25) и (26),
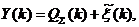 - показания октаномера; (25)
- показания октаномера; (25)
 - уравнение измерения октанового числа, (26)
- уравнение измерения октанового числа, (26)
и выше приведенных ограничений (2), (3) и (4) возникает задача оценивания параметров линейной регрессии (27) при линейных ограничениях на вектор входных переменных /3/.
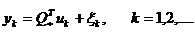 (27)
(27)
где число 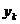 и вектор
и вектор 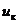 входных переменных (
входных переменных (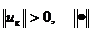 -евклидова норма вектора) предполагаются известными в каждый момент k дискретного времени,
-евклидова норма вектора) предполагаются известными в каждый момент k дискретного времени, 
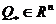 - вектор неизвестных (оцениваемых) параметров (
- вектор неизвестных (оцениваемых) параметров (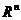 - n-мерное евклидово вещественное пространство), Т - символ транспонирования. Неизвестная величина (помеха)
- n-мерное евклидово вещественное пространство), Т - символ транспонирования. Неизвестная величина (помеха) 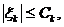 предполагается ограниченной, где
предполагается ограниченной, где 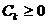 - известное число.
- известное число.
Список литературы.
- Астапов В.Н., Бакан Г.М., Сальников Н.Н. Оценивание с помощью эллипсоидов параметров линейной регрессии при линейных ограничениях на вектор входных переменных //Автоматика. – 1993. - №1. – С.28 – 34.
- Астапов В.Н., Бакан Г.М., Коцюба А.Т., Одинцова Е.А. Математическое моделирование технологического процесса смешивания бензиновых фракций //Автоматика. – 1992. - №5. – С. 31 – 37.
- Астапов В.Н. Методологические и схемотехнические решения в системах контроля и управления на нефтеперерабатывающем заводе – Самара: Изд-во СНЦ РАН, 2006. 286 с.
- Савин М.М., Елсуков В.С., Пятина О.Н. Теория атоматического управления: Учеб. пособие / Под ред. д.т.н., проф. В.И. Лачина – Ростов-на-Дону; Феникс, 2007 – 469 с.
- Лукас.В.А. Основы фази-управления: Учеб. пособие. – Екатеринбург, 2000. – 60 с.
- Нечеткие множества в моделях управления и искусственного интеллекта/ Под ред. Д.А. Поспелова – М.: Наука, 1986 – 312с.
- Мелихов А.Н., Бернштейн Л.С., Коровин С.Я. Ситуационные советующие системы с нечеткой логикой – М.: Наука, 1990 – 272с.
Date: 2015-07-17; view: 807; Нарушение авторских прав