Колебание струны

С помощью дифференциальных уравнений описываются погодные процессы (перенос теплого и холодного воздуха), конвективные процессы (процессы обмена слоями воздуха или газа в жидкости). Наличие турбулентности (присутствие вихря) приводит к тому, что трудно рассчитать в какой точке какая будет температура. Кроме уже выделенных уравнений для описания конвективных процессов добавляются ещё дополнительные уравнения, т.е. модель усложняется.

Системой дифференциальных уравнений описывают тепловые процессы в таких областях как авиа и ракетостроение. Например топливный бак подвергается значительному механическому и тепловому воздействию.

Классическая задача колебания струны состоит в следующем: струна с концами А,В закреплена в точках А и В, либо подвергается механическому воздействию в этих точках, при этом точка А или точка В начинает отклонятся от положения равновесия. Это отклонение можно обозначить какой-нибудь функцией, например функцией U. Тогда классической задачей о поведении струны при механическом воздействии называется следующая задача: решается уравнение второго порядка

которое описывает отклонение от положения равновесия точек внутри струны.

Начальные условия: 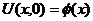(условие начального слоя)

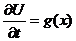
Краевые условия: 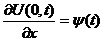- левое граничное условие

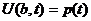- правое граничное условие.

Решить эту задачу, значит найти отклонение положения струны от равновесия, т.е. найти U в каждый момент времени.

Алгоритм

Задаём массивы (3 массива) –для хранения данных каждого из 3-х слоёв.

U1 – задаёт условия начального слоя;

U2 – определяется функцией на следующем слое (втором);

U3 – определяется значение на следующем слое (третьем).

1. U1 –задано функцией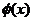

2. 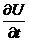_t=0 = g(x); это отсюда нам необходимо выразить U2[x] (самостоятельно)

Благодаря этому условию, мы можем посчитать значения второго слоя.

4. Открываем цикл по времени

for k;2 to n do

begin

3. Распишем основное уравнение

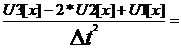
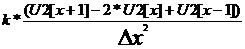
Выразив U3[x], мы можем в цикле (for x:=0 to n-1 do) посчитать все значения отклонения для каждой точки х на третьем слое, за исключением правой граничной точки на этом же слое.

4.Для нахождения значения в правой граничной точке мы используем правой граничное условие, например 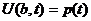, т.е. мы знаем значения в крайней правой точке стержня равной b для любого момента времени. (возможно будет дана не функция а её производная, тогда необходимо её расписать и выразить U3 в точке b).

Затем вывод U3 и переприсваивание массивов:U1:=U2, U2:=U3;

Закрываем цикл по времени.

Программа на Pascal аналогична первой (для уравнения теплопроводности), составить самостоятельно.

Date: 2015-07-17; view: 587; Нарушение авторских прав