Решение краевых задач

Опр. Краевой задачей называется задача, в которой определённым образом задано условие на краях исследуемой области. Условия определяют поведение искомой функции.

Опр. (постановка краевых задач).

Решить дифференциальное уравнение y"=f(x,y,y'), при чём обязательно заданы граничные условия. Найти значения y в каждой точке фиксированной x.

Краевые задачи делятся на разные виды в зависимости от начальных условий:

1. Если граничные условия имеют вид: y(a)=A, y(b)=B. Где А и В либо константы, либо функция, то это краевые условия первого рода.

2. Если граничные условия имеют вид: y'(a)=A, y'(b)=B, то это краевая задача второго рода.

3. Если известны комбинации: α₁·y'(a)+β₁·y(a)=γ₁ и

α₂·y'(a)+β₂·y(a)=γ₂ то это краевая задача третьего рода.

Для задач первого рода известна функция, т.е. например, известно значение температуры на краях стержня.

Для задач второго рода на границах сама функция неизвестна, а известна её производная.

Для задач третьего рода неизвестно значение функции, неизвестна производная, а известна их комбинация.

Краевые задачи делятся на три основных типа:

1. Параболического типа (пример: уравнения теплопроводности).

2. Гиперболического типа (уравнение описывающее колебание струны).

3. Эллиптического типа.

Рассмотрим краевую задачу 2-го рода параболического типа.

Задача: (моделирует процессы теплопереноса).

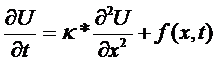
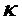- коэффициент.

f – функция внутренних тепловых источников.

U – температура.

Начальные условия:

U(x,0)=φ(x)

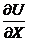_x=a = f(t) - левое граничное условие

U(b)=q(t) - правое граничное условие

Для её решения использую метод сеток.

Решение:

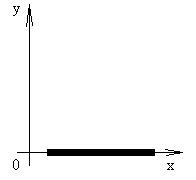Изобразим декартовую систему координат, где отложим х (точка стержня) и у (момент времени).

Рассмотрим стержень.

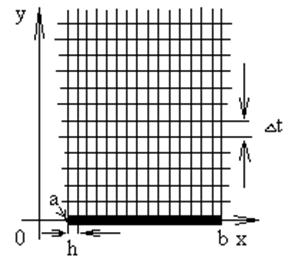Разобьем участок стержня на n равных частей и рассмотрим шаг h=(b-a)/n (см. рисунок).

Для выбора шага по времени используем условие устойчивости: 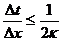это условие применяется для явной сетки, когда последующий слой считается через предыдущий. Если это условие будет не соблюдаться, то в программе могут возникать неадекватные результаты: очень большие числа или числа разных знаков. Обычно 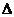t приходится выбирать очень маленьким, например 0,001, 0,0001, что затрудняет процесс счёта на компьютере. Например реальный процесс, который происходит 2 секунды моделируется на компьютере 2 часа.

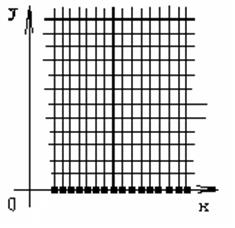Используя условие U(x,0)=φ(x) мы можем найти значение температуры в каждой точке стержня в начальный момент времени, т.е. посчитать значение в следующих узлах сетки:

Используя, правое граничное условие, мы найдём значение температуры на правом краю стержня во все моменты времени. На сетке эти точки будут расположены следующим образом:

(см. рисунок).

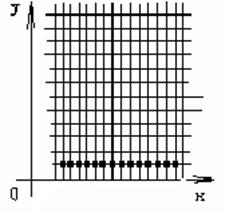
Затем, используя основное уравнение теплопроводности и выразив последующий слой через предыдущий мы можем найти значения температуры в следующих точках (см. рисунок).

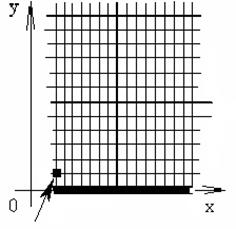И наконец распишем производную на левой границе: 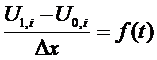Найдём значение в точке U_{0, I}:

U_{0, i} = U_{1, i} -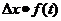

Значение в данной точке будет соответствовать следующему узлу сетки (см рисунок).

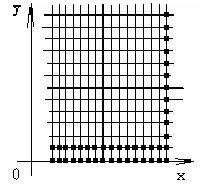Таким образом мы посчитаем значения температуры в следующих узлах (см. рисунок)

Таким образом мы можем посчитать температуру во всей сетке (во всех узлах) и будем знать температуру стержня в каждой точке стержня в каждый момент времени.(Для получения более подробных сведений обращаётесь в раздел численных методов – решение краевых задач.)

Date: 2015-07-17; view: 1886; Нарушение авторских прав