Моделирование физической и биологической задачи

Задача 1. Задача о пушке из которой надо попасть в крепость (физическая задача).

Горизонтальное x и вертикальное y – смешение снаряда за время t описывается формулами:

x = (Ư cosα) · t

y = (Ư sinα) · t – (g t² / 2)

где, g – ускорение свободного падения, t – время, α – угол наклона пушки.

Изменим математическую модель, выразим из первой формулы время t и подставим ее во вторую формулу: h = S tgα – (g S² / 2 Ư² cos²α)

Требуется найти такое значение угла α, чтобы снаряд пролетев заданное расстояние S попал на нужную высоту h.

Объяснение: Задача сводится к решению уравнения методом половинного деления, где α берется от 0 до π/4.

Метод половинного деления имеет аналог в артиллерийском приеме (пристрел) – одно положение выше цели другое ниже цели.

Задача 2. Задача о лисах и кроликах (биологическая задача).

На некотором острове живут лисы и кролики. Кролики питаются травой, а лисы охотятся на кроликов. Экологи пересчитывая кроликов и лис установили:

1) коэффициент прироста числа кроликов зависит от колебания погоды (холодная или теплая зима и т. д.) и колеблется в пределах от 3,2 до 4,7;

2) коэффициент прироста числа лис при избытки крольчатины колеблется от 5,2 до 5,7. При недостатки он пропорционален приросту кроликов.

Коэффициент пропорциональности ≈ 1/C, где C – масса крольчатины в среднем съедаемая одной лисой за год (примем за 50).

Требуется установить как меняется численность кроликов и лис с течением времени

Построение модели:

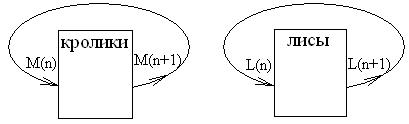
M(n) – масса кроликов через n лет.

L(n) – масса лис через n лет.

Взаимодействие лис и кроликов:

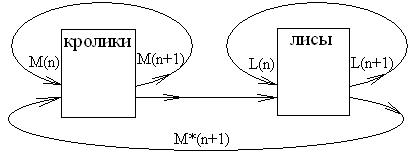
В этой динамической системе усматривается три контура обратной связи. Опишем их расчетными формулами.

Кролики: прирост иде6т в соответствии с моделью неограниченного роста. Их поедают лисы, поэтому изменение кроликов можно записать так:

M(n+1) – M(n) = k · M(n) – C · L(n)

M(n+1) = (1+k) · M(n) – C · L(n)

Лисы: если кроликов очень много, то численность кроликов растет по модели ограниченного роста, а численность лис тоже растет по модели неограниченного роста. Если крольчатины мало, то прирост определяется величиной, 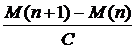показывающей сколько новых лис может прокормиться за счет прироста кроликов.

Для лис можно вывести формулу:

L(n+1) – L(n) = min (a, 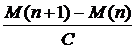) · L(n)

L(n+1) = (1 + min (a, 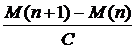)) · L(n)

где a- коэффициент неограниченного роста кроликов.

Заполнить электронную таблицу следующими данными:

a = 0.1

k = 4

C = 50

M(0) = 10000

L(0) = 100

Узнать, сколько кроликов и лис будет через 5 лет, 10 лет. Построить графики L(n) и M(n) как функция от n.

Date: 2015-07-17; view: 637; Нарушение авторских прав