Моделирование в среде MathCAD задачи «Хищники и жертвы»

В 1925 г. В Италии образовался союз двух учённых: математика Вито Вольтер и зоолог Д’Анконо. Рассматривалась задача о явлении, связанном с периодическим в несколько лет возрастанием и убыванием улова промысловых рыб. Статистика привела к следующему выводу: в период 1ой мировой войны интенсивность рыбной ловли в средиземном море резко снизилась, что привело к возрастанию числа хищных рыб, питающихся промысловыми рыбами. В результате численность промысловых рыб резко упала, что в свою очередь привело к гибели части хищных рыб, потому что их пища стала исчезать.

Обсуждая данное явление они пришли к выводу, что помимо внешних факторов (смена времён года, климата) существует причины особого характера, влияющие на популяции животных.

Качественно описать словами данный процесс не представляется возможным, необходимо выразить явления с помощью формул и уравнений. Были проанализированы различные виды животных в разных местах планеты и сделаны следующие допущения модели:

1.пища (жертва) неограниченна средой обитания.

2.хищники питаются только жертвами.

3. прирост жертв пропорционален их численности.

4.убыль жертв пропорциональна произведению числа жертв и хищников.

5.прирост хищников пропорционален произведению числа хищников и жертв.

6.убыль хищников пропорциональны их числу.

Модель такого биоценоза с учётом введённых допущений определяется следующей системой из двух дифференциальных уравнений:

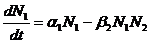(1)

N₁ -жертвы (их число).

t- время

N₂- число хищников.

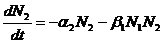(2)

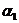- коэффициент естественного прироста жертв.

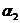- коэффициент естественного прироста хищников.

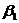-коэффициент уничтожения хищниками жертв.

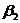-коэффициент защиты жертв от хищников.

Приведём уравнения 1 и 2 к нормированному виду:

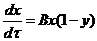
где 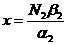относительное число жертв.

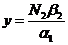относительное число хищников.

τ- нормированное время.

B= 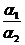- коэффициент.

Составим по данной математической модели программу на языке MathCAD (см практику).

Date: 2015-07-17; view: 957; Нарушение авторских прав