Укрупненная схема моделирующего алгоритма А - схемы

Данная схема построена по принципу .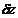

1) ввод исходных данных

2) установка начальных условий

3) определение ближайшего особого состояния

4) продвижение системного времени

5) проверка условия окончания моделирования

6) обработка особого состояния агрегатов

7) передача сигналов между агрегатами

8) фиксация промежуточных результатов

9) проверка наличия входных сигналов

10) выбор агрегата, имеющего сигналы на входе

11) просмотрены все агрегаты А – схемы

12) обработка особого состояния агрегата

13) обработка результатов моделирования

14) вывод результатов моделирования

Блок – схема алгоритма блока № 6(12)

6.1 – какой тип агрегата

6.7 – стереть входной сигнал

Блок 6 выбирает тип агрегата, для которого реализуется дальнейшее продвижение по моделированию.

Блок – схема алгоритма блока № 6.2

1 – какое событие произошло?

1а – поступил входной сигнал

1б – наступило время выдачи заявки

2 – выдать новую заявку

3 – генерировать интервал времени между заявками

Блок – схема алгоритма блока № 6.3

1 – какое событие произошло

1а – закончилось обслуживание заявки

1б – поступил входной сигнал

2 – разрешение на выдачу заявки

3 – разрешить выдачу заявки

4 – запрещение на выдачу заявки

5 – запретить выдачу заявки

6 – поступление заявки

7 – обслуживание заявки в канале

8 – можно выдать заявку?

9 – выдать заявку из канала

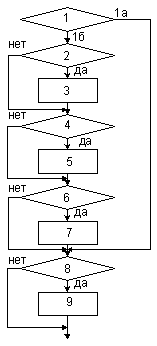
Блок – схема алгоритма блока № 6.5

10) запрещение на выдачу заявки

11) запретить выдачу заявки по данному направлению

12) разрешение на выдачу заявки

13) разрешить выдачу заявки по данному направлению

14) поступила заявка?

15) разрешена передача по направлению?

16) выдать заявку по направлению 1

17) ошибка в связях между агрегатами

18) разрешена передача по направлению?

10) выдать заявку по направлению 2

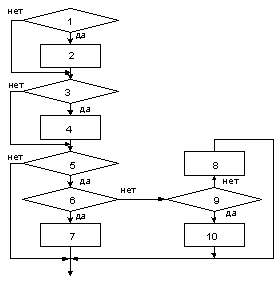
Блок – схема алгоритма блока № 6.6

заявка поступила

12) можно выдать заявку?

13) пустой сигнал с направления 1

14) разрешить выдачу по направлению 2

15) пустой сигнал с направления 2

16) выдать пустой сигнал

17) выдать заявку

18) ошибки в связях между агрегатами

19) блокировка на выдачу заявки

20) запретить выдачу заявки

21) разрешить выдачу заявки по направлению 1

Общие вопросы планирования эксперимента. Полный факторный эксперимент. Формирование матрицы планирования эксперимента.

Полным факторным экспериментом (ПФЭ) называется такой эксперимент, при реализации которого определяется значение функции цели или всех возможных сочетаний уровней варьирования факторов.

Если имеется К факторов, каждый из которых может устанавливаться на 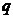уровнях, то для осуществления ПФЭ необходимо поставить опытов.

Наибольшее распространение получили эксперименты, в которых факторы варьируются на двух уровнях, т.е. эксперименты типа 2^к.

Планирование, проведение и обработка результатов ПФЭ состоит из следующих обязательных этапов:

- кодирование факторов;

- составление плана-матрицы эксперимента;

- реализация плана эксперимента;

- проверка воспроизводимости опытов;

- расчет коэффициентов регресси линейной модели;

- проверка адекватности линейной модели;

- оценка значимости коэффициентов регрессии.

Кодирование факторов необходимо для перевода натуральных факторов в безразмерные величины. Такой перевод, выполняется для того, чтобы иметь возможность построить стандартную ортогональную матрицу планирования эксперимента.

Составление плана-матрицы начинают с выбора влияющих факторов.

После выбора факторов для каждого из них устанавливается основной уровень (среднее, исходное значение) и интервал варьирования. Затем определяют верхний уровень фактора путем прибавления к основному уровню интервала варьирования; и нижний уровень фактора – путем вычитания интервала варьирования из основного уровня.

Основной уровень обозначается 0;

Верхний уровень +1;

Нижний уровень -1;

Интервал варьирования рекомендуется выбирать таким образом, чтобы он не превышал удвоенной средней арифметической ошибки в определении данного фактора.

После выбора уровней факторов составляют план-матрицу эксперимента.

Пример: в данном примере варьируются два фактора Х₁ и Х₂ на двух уровнях: +1, -1.

План-матрица приведена в табл.Строки этой таблицы соответствуют различным опытам, а столбцы – значениям факторов.

Таблица

План-матрица эксперимента

Номер опыта	Х1	Х2	Х1Х2	Yn1	Yn2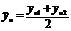
	-1	-1	+1	27.0	28.0	27.5
	+1	-1	-1	15.9	17.1	16.5
	-1	+1	-1	22.1	22.9	22.5
	+1	+1	+1	13.4	13.6	13.5

В столбцах 2 и 3 таблица записаны уровни факторов варьирования.

В процессе реализации плана эксперимента заполняются столбцы 5 и 6. Причем эксперимент проводится два раза. В столбце 7 записывается вычисленное среднее значение двух серий эксперимента 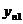и , характеризующих износ деталей агрегата.

Матрицу такого типа называют расширенной матрицей планирования эксперимента, т.к. введен столбец Х₁Х₂, позволяющих оценить коэффициент регрессии при взаимодействии факторов.

Планирование эксперимента. Проведение опытов и проверка воспроизводимости параллельных опытов.

Проверка воспроизводимости параллельных опытов при одинаковом их числе на каждом сочетании уровней факторов осуществляется по критерию Кохрена

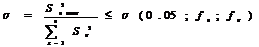(1)

где 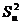- дисперсия, характеризующая рассеивание результатов опытов на u– м сочетании уровней факторов.

Процесс считается воспроизводимым, если выполняется неравенство (1). Если же неравенство (1) не выполняется, то необходимо уточнить измерения в опытах с максимальными дисперсиями .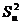

Планирование эксперимента. Расчет коэффициентов регрессии и проверка их значимости.

В случае воспроизводимости процесса переходят к расчету коэффициентов регрессии

.

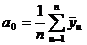
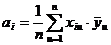
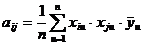Затем строят линейную модель эксперимента:

^.

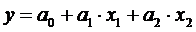Далее необходимо выполнить оценку значимости коэффициентов регрессии с помощью критерия Стьюдента. Коэффициент считается значимым, если выполняется неравенство

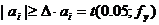
где 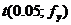– табличное значение критерия Стьюдента.

Планирование эксперимента. Проверка адекватности математической модели.

После расчета коэффициентов регрессии необходимо проверить адекватность модели с помощью критерия Фишера. Модель считается адекватной, если имеет место неравенство

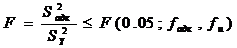
где

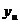- расчетное значение отклика в u -м опыте;

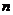- количество опытов;

F(0,05, f_адкf_т) - критерий Фишера при 5% -м уровне зависимости;

f_адк = n-k-1 - число степеней свободы дисперсии адекватности;

k - количество факторов;

f_u - число степеней свободы дисперсии воспроизводимости.

Модель считается адекватной, если значение F, полученное по формуле, не превышает соответствующего табличного значения при заданном уровне значимости.

Планирование эксперимента. Построение математической модели в натуральных единицах.

Полученные выше регрессионные математические модели являются нормированными, т.к. значения факторов в них могут принимать значения от –1 до +1.

Для практического использования математической модели, удобнее, когда в ней принимают натуральные значения.

Пересчет коэффициентов модели к натуральным значениям факторов производится на основании выражения нормирования факторов

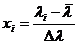
где 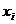– i-ое нормированное значение фактора;

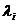- i-й (нижний или верхний) уровень фактора;

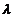- нулевой уровень фактора;

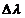- интервал варьирования..

Откуда .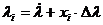

Планирование эксперимента. Понятие дробного факторного эксперимента. Построение матрицы планирования дробного факторного эксперимента.

С увеличением числа факторов, количество опытов в полном факторном эксперименте резко возрастает. Так при трех факторах необходимо поставить 2³ =8 опытов, при восьми – 256 и т.д.

Поэтому целесообразно сократить число опытов за счет информации, которую несут эффекты взаимодействия факторов и которая для построения линейной модели несущественна.

Рассмотрим ПФЭ 2².

ПФЭ 2к	№ опыта	Факторы	Параметры
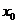
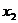
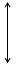
		+1	+1	+1	Y1
22		+1	-1	+1	Y2
		+1	+1	-1	Y3
		+1	-1	-1	Y4

По нему можно построить модель:

.

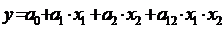Однако, если процесс описывается линейной моделью, то достаточно определить только 3 коэффициента: a_0; a_1; a₂, a квадратичный коэффициент а₁₂ будет достаточно малым.

Если включить в матрицу планирования вместо столбца x₁x₂ фактор х₃, то получится матрица планирования для трех факторов, линейная модель которой

.

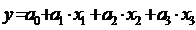Коэффициенты этой модели рассчитываются по формулам, где коэффициент 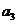совпадает со значением .

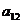36.Регрессионный и корреляционный анализ. Обработка результатов натурного и расчетного эксперимента. 248