Проверка качества псевдослучайных последовательностей чисел. Проверка стохастичности и независимости

Проверка стохастичности последовательностей псевдослучайных чисел 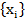наиболее часто проводится методами комбинаций и серий.

Сущность метода комбинаций сводится к определению закона распределения длин участков между единицами (нулями) или закона распределения (появления) числа единиц (нулей) в п-

разрядном двоичном числе 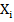. На практике длину последовательности 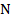берут достаточно большой и проверяют все и разрядов или только 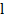старших разрядов числа .

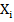Теоретически закон появления у единиц в 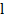разрядах двоичного числа 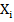описывается исходя из независимости отдельных разрядов биномиальным законом распределения: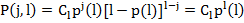

где 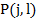— вероятность появления 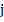единиц в 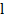разрядах числа 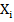; 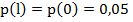— вероятность появления единицы (нуля) в любом разряде числа ; .

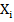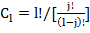Тогда при фиксированной длине выборки 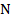теоретически ожидаемое числопоявления случайных чисел 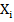с 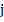единицами в проверяемых 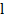разрядах будет равно .

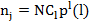После нахождения теоретических и экспериментальных вероятностей 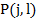иличисел 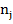при различных значениях 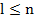гипотеза о стохастичности проверяется с использованием критериев согласия.

При анализе стохастичности последовательности чисел 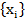методом серий последовательностьразбивается на элементы первого и второго рода (а и b), т. е. .

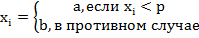Серией называется любой отрезок последовательности, состоящий из идущихдруг за другом элементов одного и того же рода, причем число элементов в отрезке (а или b) называется длиной серии.

После разбиения последовательности 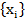на серии первого и второго рода будемиметь, например, последовательность вида...aabbbbaaabaaaabbbab....

Так как случайные числа а и bв данной последовательности независимы и принадлежатпоследовательности 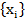, равномерно распределенной на интервале (0, 1), то теоретическая вероятность появления серии длиной 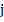в последовательности длиной 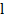в 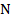опытах (под опытом здесь понимается генерация числа 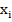, и проверка условия 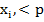) определится формулой Бернулли: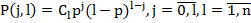

В случае экспериментальной проверки оцениваются частоты появления серийдлиной 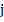. В результате получаются теоретическая и экспериментальная зависимости 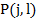, сходимость которых проверяется по известным критериям согласия, причем проверку целесообразно проводить при различных значениях 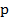, 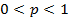и .

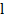Проверка независимости элементов последовательности псевдослучайных квазиравномернораспределенных чисел проводится на основе вычисления корреляционного момента.

Случайные величины 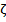и 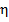называются независимыми, если закон распределениякаждой из них не зависит от того, какое значение приняла другая. Таким образом, независимость элементов последовательности 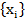может быть проверена путем введения в рассмотрение последовательности 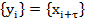, где 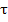— величина сдвига последовательностей.

В общем случае корреляционный момент дискретных случайных величин 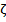и 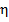с возможными значениям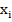и , и 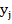определяется по формуле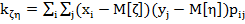

где 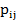— вероятность того, что 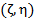примет значение .

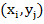Корреляционный момент характеризует рассеивание случайных величин 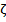и 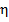и их зависимость. Если случайные числа независимы, то . Коэффициенткорреляции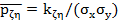

где 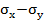— средние квадратические отклонения величин 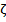и .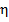

При проведении оценок коэффициента корреляции на ЭВМ удобно для вычисленияиспользовать следующее выражение: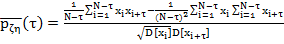

где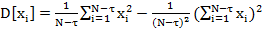

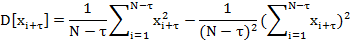
При вычислениях сначала рационально определить суммы: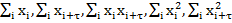

При любом 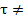для достаточно больших 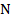с доверительнойвероятностью 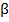справедливо соотношение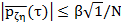

Если найденное эмпирическое значение 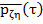находится в указанных пределах, то с вероятностью 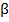можно утверждать, чтополученная последовательность чисел 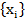удовлетворяет гипотезе корреляционной независимости.

11.Моделирование случайных процессов с заданной корреляционной функцией.

Непрерывно-стохастические модели. Q - схемы. Основные понятия обслуживания. Понятие прибора обслуживания.

Непрерывно-стохастический подход рассмотрим на основе систем массового обслуживания, которые будем называть Q – схемами. Системы массового обслуживания представляют собой класс математических схем, разработанных в теории массового обслуживания для формализации процессов функционирования систем, которые по своей сути являются процессами обслуживания.

В качестве процесса обслуживания могут быть представлены процессы функционирования экономических, технических, производственных и других систем.

Характерным для работы таких объектов является стохастический характер процесса их функционирования, т.е. случайное появление заявок на обслуживание и завершение обслуживания в случайные моменты времени.

В любом элементарном акте обслуживания можно выделить две основные составляющие:

1.Ожидание обслуживания заявкой;

2.Собственно обслуживания заявки.

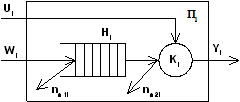Это можно изобразить в виде некоторого i-го прибора обслуживания П_i, состоящего из накопителя заявок Н_i, канала обслуживания К_i.

В накопителе заявок может одновременно находится 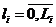заявок, где L_i – емкость i-го накопителя.

На каждый прибор обслуживания П_i поступают потоки событий:

- в накопитель Н_i потоки заявок ω_i;

- в канал К_i – поток обслуживаний U_i.

Потоком событий называется последовательность событий, происходящих одно за другим в случайные моменты времени.

Различают потоки однородных и неоднородных событий.

Поток событий называется однородным, если он характеризуется только моментами наступления этих событий (вызывающими моментами) и задаются последовательностью {t_n} = {0 ≤ t₁≤ t₂ … ≤ t_n≤ …},

где t_n – момент наступления n-го события.

Однородный поток событий может быть задан также в виде последовательности промежутков времени между n-м и (n-1)-м событиями {τ_n}, которая однозначно связана с последовательностью вызывающих моментов {t_n} следующим образом: τ_n = t_n – t_n-1, Например, при n = 1 и t_o = 0, τ₁ = t₁;

при n = 2 τ₂ = t₂ - t₁. и т.д.

Потоком неоднородных событий называется последовательность {t_n, f_n}, где t_n – вызывающие моменты; f_n – набор признаков события (наличие приоритета; возможность обслуживания тем или иным типом канала и т.д.).

Заявки, обслуженные каналом К_i, и заявки, покинувшие прибор П_i по различным причинам необслуженными (например, из-за переполнения накопителя), образуют выходной поток y_i Î Y.

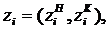Процесс функционирования прибора обслуживания П_i можно представить как процесс изменения состояний его элементов во времени z_i(t). Переход в новое состояние для прибора П_i означает изменение количества заявок, которые в нем находятся (в канале К_j и накопителе Н_i).

Вектор состояний для прибора П_i имеет вид

где 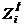- состояние накопителя (0 – накопитель пустой, n – в накопителе n заявка, L^н – накопитель заполнен);

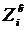- состояние канала (0 – канал свободен, 1 – канал занят, 2 – канал заблокирован).

Date: 2015-07-17; view: 1650; Нарушение авторских прав