Понятие агрегата. Основные параметры (множества), характеризующие агрегаты. Описание процесса функционирования агрегата

Обобщенный (универсальный) подход базируется на понятии агрегативной системы. Она представляет собой формальную схему общего вида, которую называют А – схемой.

Приагрегативном описании моделируемый объект (система) декомпозируется на конечное число подсистем с сохранением связей, которые обеспечивают их взаимодействие. В результате декомпозиции, система представляется в виде многоуровневой конструкции из взаимосвязанных элементов, которые объединяются в подсистемы различных уровней. В качестве элемента А – схемы выступает агрегат.

Каждый агрегат A_n, 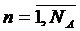характеризуется:

T – множеством моментов времени

X – множеством входных сигналов

Y – множеством выходных сигналов

Z – множеством состояний

Процессы перехода агрегата из одного состояния в другое происходит за малый промежуток времени, т.е. имеет место скачек состояний 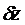, т.е. переход из состояния z(t₁) в состояние z(t₂) происходит скачком (z(t₂)≠z(t₁)).

Эти переходы определяются собственными (внутренними) параметрами схемы и входными сигналами .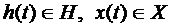

В начальный момент времени t₀ состояние z⁰=z(t₀) задается распределением L[z(t₀)].

Предполагая, что процесс функционирования агрегата в моменты поступления входных сигналов Х_n описываются случайным оператором V:

z(t_n+0)=V[t_n, z(t_n), x_n], где t_n+0 – скачок, t_n – момент поступления входного сигнала.

Процесс функционирования (t_n,t_n+1), t 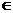(t_n,t_n+1) описывается случайным оператором :

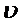z(t)= 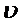[t, t_n, z(t_n+0)]

Наоператор 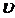не накладывалось никаких ограничений, поэтому допустимы скачки состояний 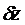в моменты времени, которые не являются моментами поступления входных сигналов. Моменты скачков будем называть особыми моментами времени 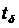, а состояния 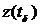- особыми состояниями, тогда:

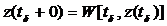
W – частный случай оператора .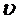

На множестве Z выделяется Z^(Y), что если 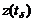достигает Z^(Y), то это является моментом выдачи выходного сигнала.

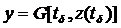, где G – некоторый случайный оператор.

A_n=<T,X,Y,Z, Z^(Y),H,V, 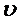,W,G> - описание отдельного агрегата.

При моделировании реальных систем применяют А-схемы, которые представляют собой конструкции из отдельных агрегатов, связи между ними задаются с помощью оператора сопряжения R.

Date: 2015-07-17; view: 1207; Нарушение авторских прав