Расчет статистических характеристик большой выборочной совокупности через центральное отклонение

Центральное отклонение показывает, насколько каждая из вариант выборки отличается от среднего значения этой выборки. Для выборки, разделенной на классы, находят различия между средними значениями классов и средним значением выборки, а затем полученные отклонения умножают на частоты классов, чтобы учесть особенности распределения.

Таблица строится на основании данных точковки.

Таблица 5

Вспомогательная таблица для расчета статистических характеристик большой выборочной совокупности через «центральное отклонение»

х	n	x×n	x2×n		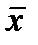a	α×n	α2×n
9,95		59,70	594,015		-5,927	-35,562	210,77597
11,65		209,70	2443,005		-4,227	-76,086	321,61552
13,35		293,70	3920,895		-2,527	-55,594	140,48604
15,05		466,55	7021,578		-0,827	-25,637	21,201799
16,75		418,75	7014,063	15,877	0,873	21,825	19,053225
18,45		369,00	6808,050		2,573	51,46	132,40658
20,15		342,55	6902,383		4,273	72,641	310,39499
21,85		87,40	1909,690		5,973	23,892	142,70692
23,55		70,65	1663,808		7,673	23,019	176,62479
S		2318,00	38277,485			-0,042	1475,27

Расчет статистических характеристик:

а) среднеарифметическая величина:

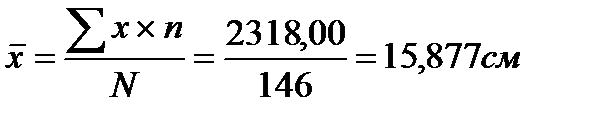
б) среднеквадратическая величина:

в) основное (среднеквадратическое) отклонение характеризует рассеяние вариант выборки относительно средней арифметической. Оно учитывает изменчивость каждого значения и выражается в тех же единицах, что и среднеарифметическая величина:

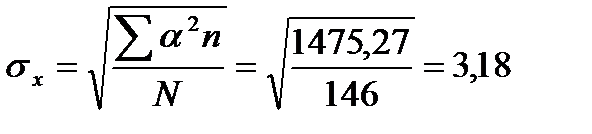см.

Использование среднеквадратического отклонения оправдано при оценке изменчивости в одной выборке или в выборках с близкими среднеарифметическими величинами. При сравнении изменчивости различных показателей применение основного отклонения может повлечь неверные выводы.

г) в том случае, когда требуется сравнение двух выборочных совокупностей по степени изменчивости применяется процентное выражение среднеквадратического отклонения от среднеарифметической величины – коэффициент изменчивости, который рассчитывается по формуле:

;

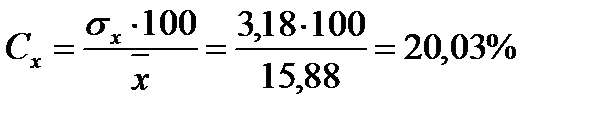д) при исследовании статистических совокупностей неизбежны некоторые отличия между генеральной совокупностью и ее частью – выборочной совокупностью. Эти различия характеризуются величиной основной ошибки:

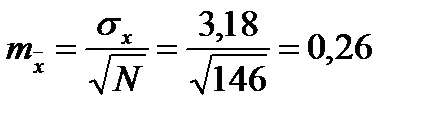см.

Общепринятый способ записи статистических показателей обязательно включает основную ошибку для этого показателя:

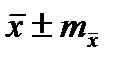
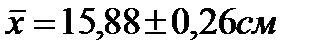
Для оценки достоверности вывода применяется критерий, определяемый отношением величины к ее основной ошибке:

e) критерий достоверности показателя:

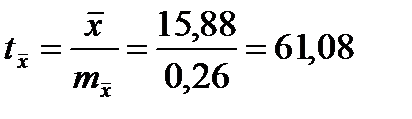
Показатель считается достоверным, если критерий больше 3.

ж) точность опыта показывает процент расхождения генеральной и выборочной средней величины, выраженный в процентах:

.

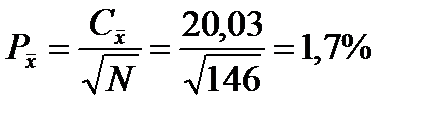Приведенные статистические характеристики достаточны для получения представления об основных параметрах выборочной совокупности и обоснования достоверности полученных данных.

Для более подробной характеристики выборочной совокупности требуется либо более усложненный вариант расчетов по приведенному методу, либо применение других методов расчета.