Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Метод Симпсона
|
|
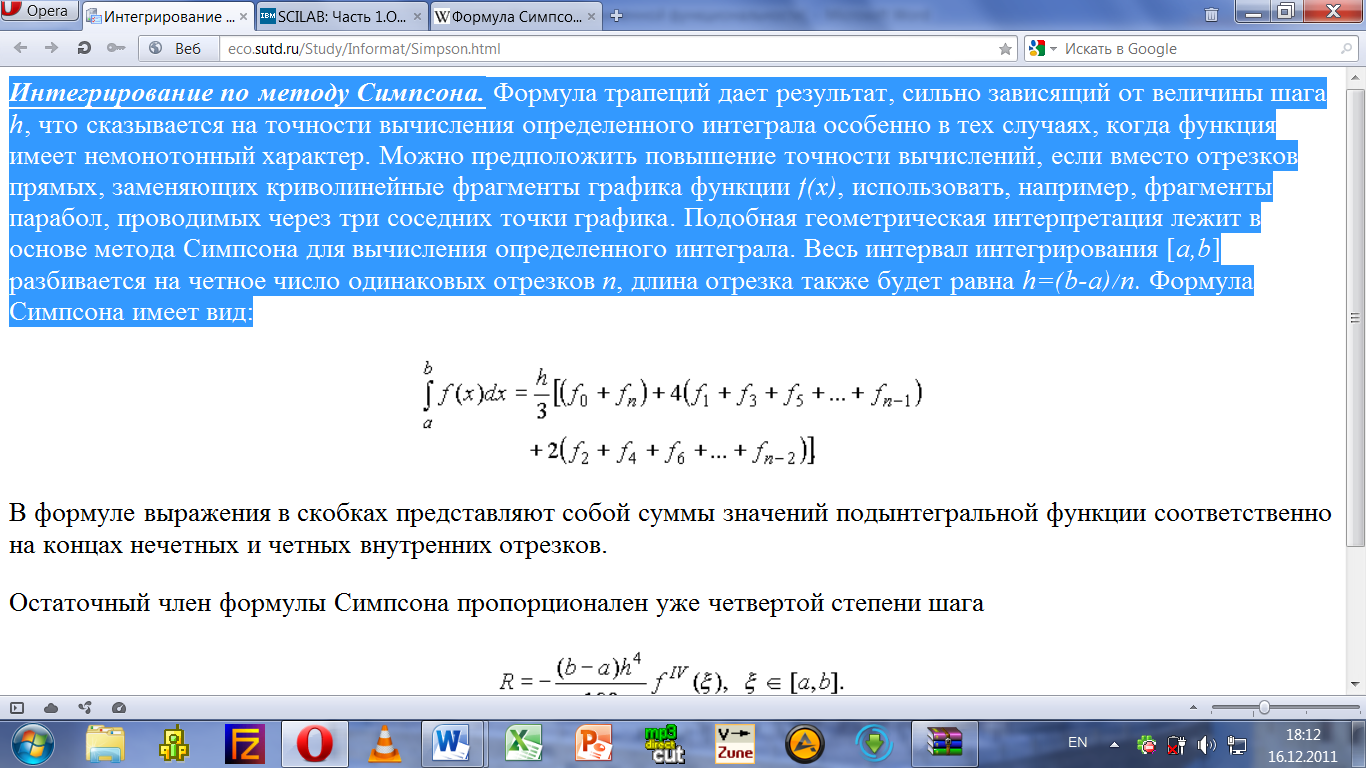
Интегрирование по методу Симпсона. Формула трапеций дает результат, сильно зависящий от величины шага h, что сказывается на точности вычисления определенного интеграла особенно в тех случаях, когда функция имеет немонотонный характер. Можно предположить повышение точности вычислений, если вместо отрезков прямых, заменяющих криволинейные фрагменты графика функции f(x), использовать, например, фрагменты парабол, проводимых через три соседних точки графика. Подобная геометрическая интерпретация лежит в основе метода Симпсона для вычисления определенного интеграла. Весь интервал интегрирования [a,b] разбивается на четное число одинаковых отрезков n, длина отрезка также будет равна h=(b-a)/n. Формула Симпсона имеет вид:
Задача 1:
1. Составить программу и вычислить на ЭВМ интеграл заданной функции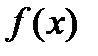 
на отрезке 
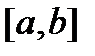с точностью 
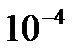методом Монте-Карло и методом Симпсона. Сравнить точность полученных результатов с точным значением интеграла.
2. Определить, какое число отрезков разбиения для метода Симпсона обеспечило бы достижение точности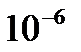 
.
Решение:
| Вариант | Подынтегральная функция f(x) | Пределы интегрирования | ||||
| a | b | |||||
| ||||||
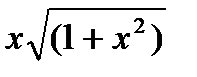
1. Вычислим точное значение интеграла:
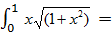0.5309799
Программа вычисления на ЭВМ интеграла заданной функции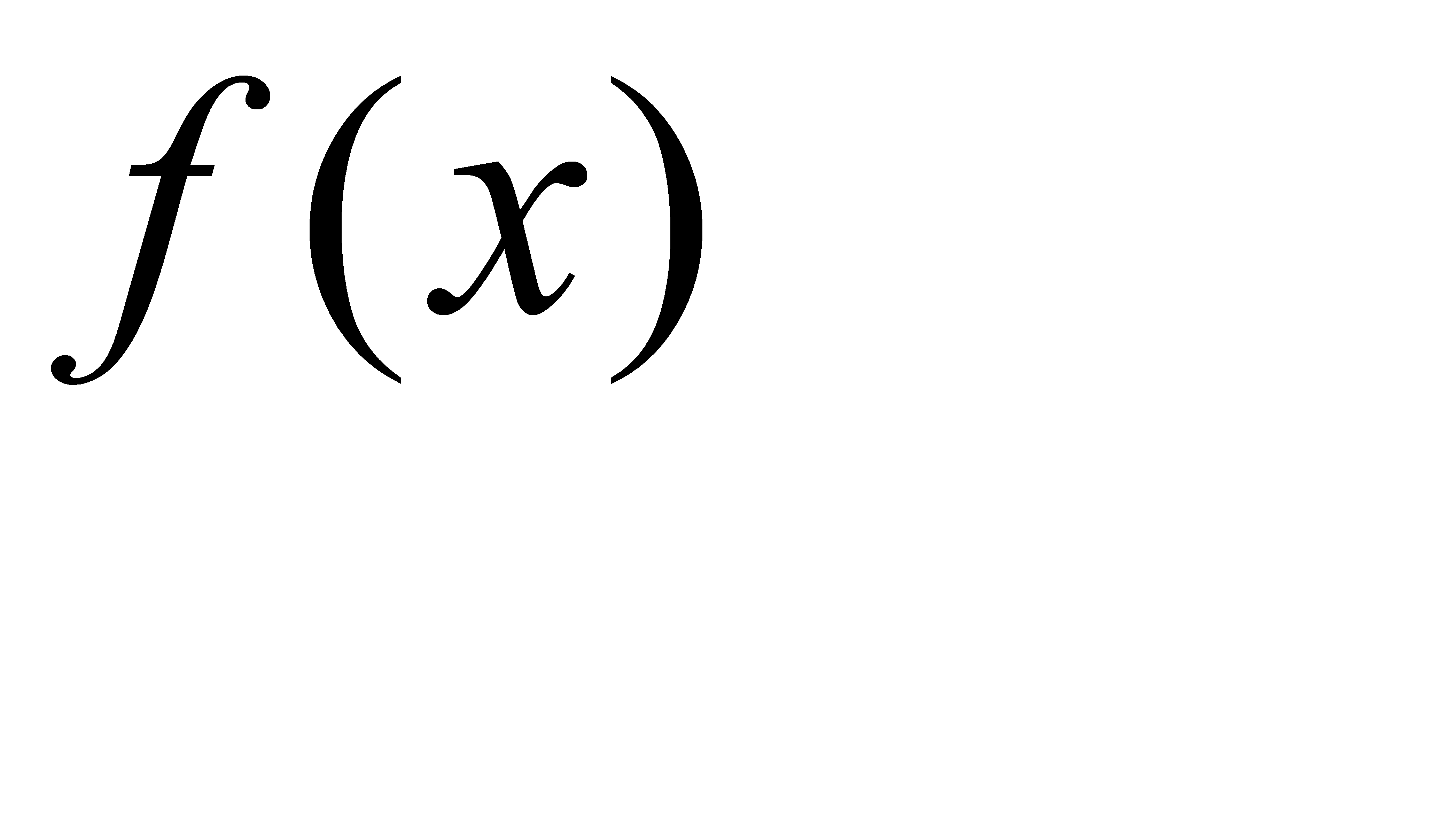 
на отрезке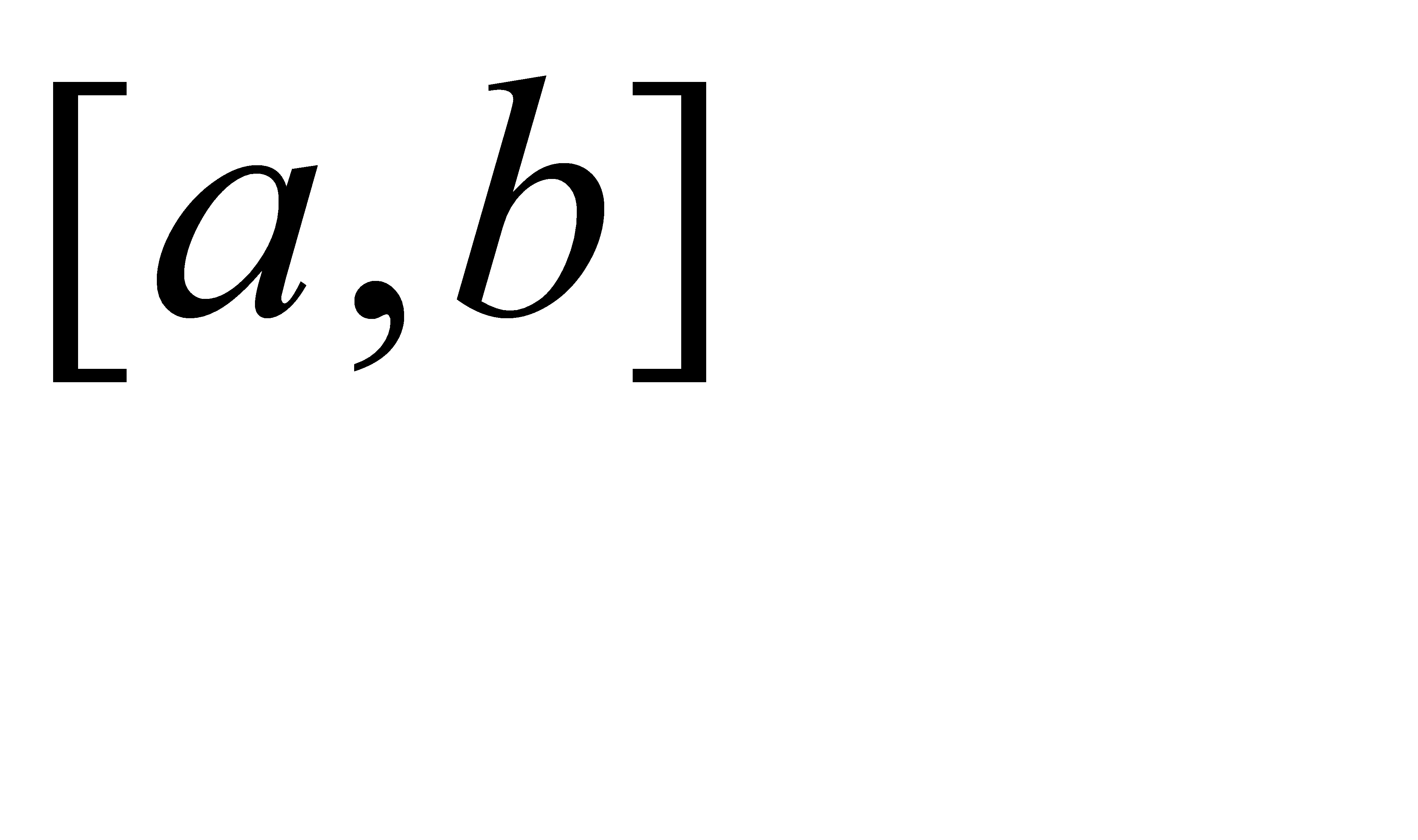 
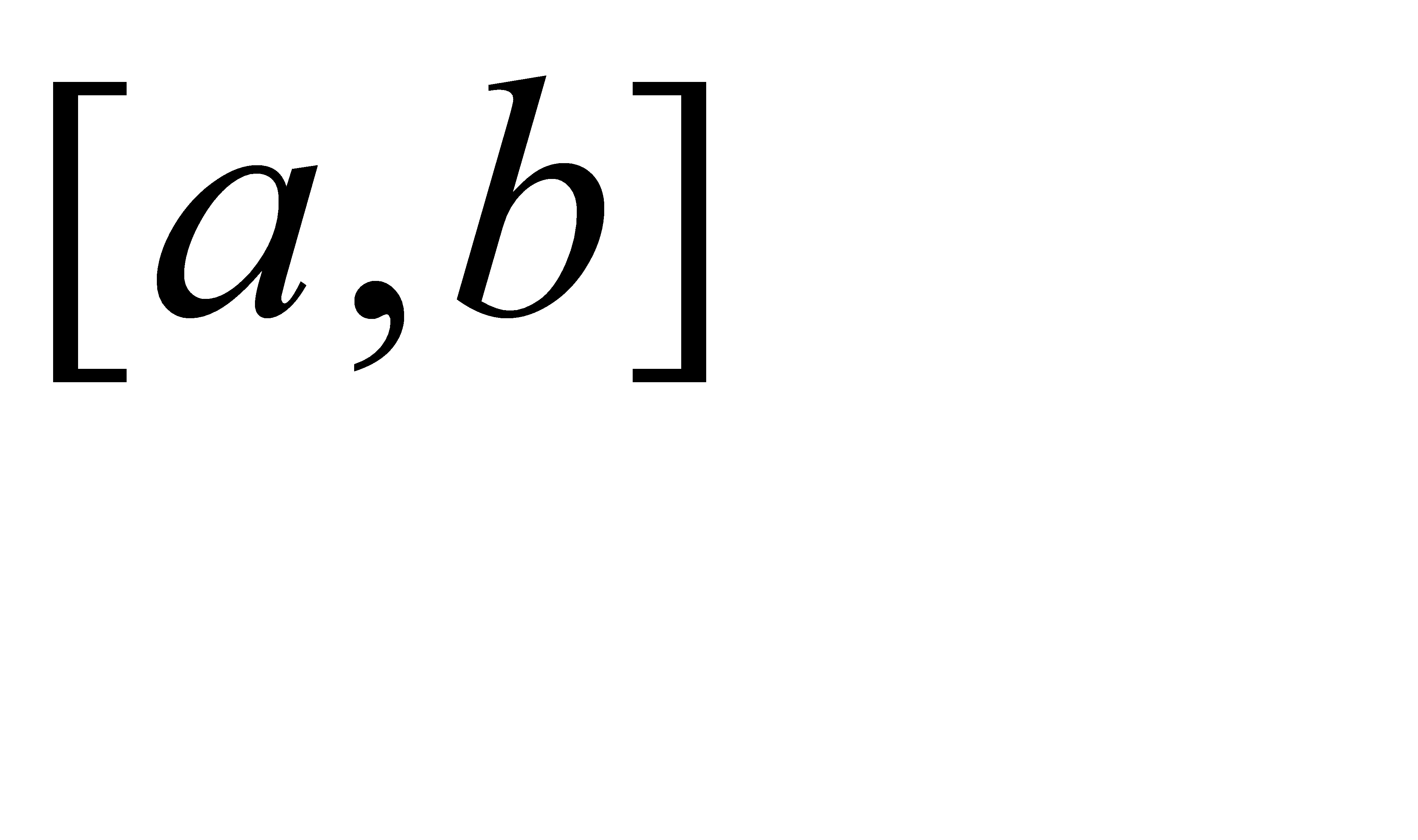с точностью 
методомМонте-Карло.
function y = monte (a, b, N, func)
S=0;
fori=1: N
S=S+ func (rand()*(b - a)+ a);
end
y =S*(b - a)/ N
endfunction
function y = myf (x), y = x*sqrt(x*x+1) endfunction
printf ('Интеграл по методу Монте-Карло =%.8f ', monte (0,1,100000,myf));
Интеграл по методу Монте-Карло = 0.5224005
Погрешность: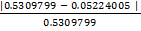 
= 0,000008317911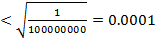 
Методсимпсона:
function y = simpson (a, b, N, func)S1=0;S2=0;fori=1:+2: N -1S1=S1+ func (a +i*(b - a)/ N)endfori=2:+2: N -2S2=S2+ func (a +i*(b - a)/ N)endh=(b - a)/ Ny =h/3*(func (a)+ func (b)+4*S1+2*S2)endfunction
0.5309805
Погрешность: 
0.0000000006
2. Определить, какое число отрезков разбиения для метода Симпсона обеспечило бы достижение точности .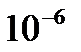
Погрешность метода Симпсона вычисляется по формуле:
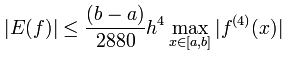
Для получаения максимального значения 4й переменной найдём её точки экстремума на промежутке [a,b]
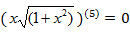при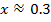 
Тогда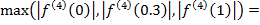 
=max(|0.8264|,|0.553|,|-0.9646|)=0.553
Отсюда:
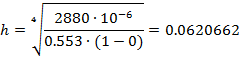
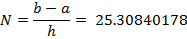
Точность 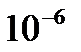будет достигаться при N=26 отрезках.
Проверим: printf('%.8f',simpson(0,1,26,myf))
0.05311069
Погрешность: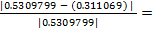 
0.0000001269<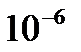
Задача 2:
1. Построить графики функций.
2. Найти площадь фигуры, ограниченной этими графиками (с точностью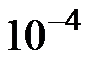 
) методом Монте-Карло. Расчет точек пересечения заданных функций и расчет интегралов оформить отдельными программами.
| Вариант | Заданные функции | ||
| 
| 
|
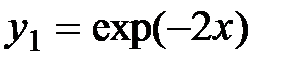
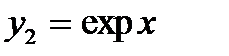
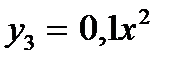
Решение:
1. Построить графики функций.
function y = y1 (x), y =exp(-2*x)endfunctionfunction y = y2 (x), y =-sqrt(9- x ^2)endfunctionfunction y = y3 (x), y =0.1*x^2endfunctionfunction y = y4 (x), x= 0.8endfunction x=[0:0.01:1] plot (x,y1(x)) plot (x, y2 (x)) plot (x, y3 (x))
y4=[0,3]
x=[0.8,0.8];
plot (x,y4)
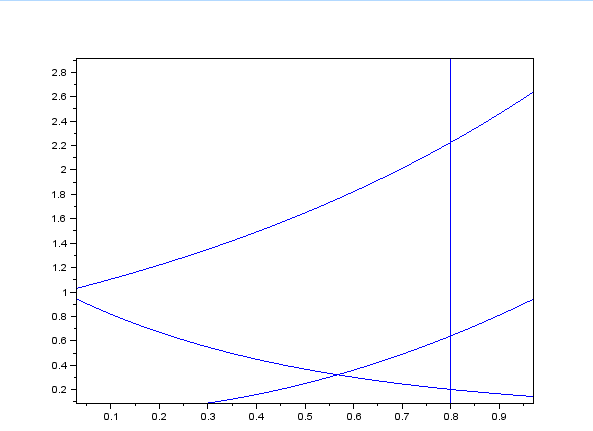
2. Найдёмточкипересечения:
function z = f1 (x, y), z =exp(-2* x)- y endfunctionfunction z = f2 (x, y), z = y -exp(x)endfunctionfunction z = f3 (x, y), z =y-0.1*x^2endfunctionfunction z = f4 (x, y), z =0.8- x endfunction function[ y ]= intersect1 (x) y (1)= f1 (x (1), x (2)) y (2)= f2 (x (1), x (2))endfunction function[ y ]= intersect2 (x) y (1)= f1 (x (1), x (2)) y (2)= f4 (x (1), x (2))endfunction function[ y ]= intersect3 (x) y (1)= f2 (x (1), x (2)) y (2)= f4 (x (1), x (2))endfunction function[ y ]= intersect4 (x) y (1)= f2 (x (1), x (2)) y (2)= f3 (x (1), x (2))endfunctionfsolve([-1,1],intersect1)
ans =
fsolve([0.5,1],intersect2)
ans =
0.8
fsolve([0.1,2],intersect3)
ans =
0.8
fsolve([0.4,0.7],intersect4)
ans =
0.576
Min(x) = 0Max(x) = 0.8Min(y) = 0.23Max(y)= 2.23
Программа для нахождения площади методом Монте-карло:
function Sq = monte2d (funcs, N, xt, rect)fori=1:length(funcs)z(i)=sign(funcs (i)(xt (1), xt (2)))endS=0forj=1: N t(1)=rand(1,1,'uniform') *(rect (3)- rect (1))+ rect (1)t(2)=rand(1,1,'uniform') *(rect (4)- rect (2))+ rect (2)flag=1fori=1:length(funcs)if~(sign(funcs (i)(t(1),t(2)))==z(i))thenflag=0endendS=S+flagend Sq =S*(rect (3)- rect (1))*(rect (4)- rect (2))/ N endfunction
Вкачестве точки принадлежащей области возьмём [2.5,0]
monte2d(list(f1,f2,f3,f4),100000000,[2.5,0],[0.0498,-1.0353,3,2.9996])
ans =
2.458764
Для оценки точности в качестве реальной площади возьмём площадь, вычесленную методом симпсона:
t=fsolve([0.1,3], intersect1)g(1)=t(1)t=fsolve([3,-1], intersect1)g(2)=t(1)t=fsolve([0.1,2], intersect2)g(3)=t(1)t=fsolve([2,-1], intersect2)g(4)=t(1) printf ('%.7f', simpson (g(1),3,100000, y21)- simpson (g(1),g(3),100000, y1)- simpson (g(3),2,100000, y31)-(simpson (g(2),3,100000, y22)+ simpson (g(4),g(2),100000, y1)- simpson (g(4),2,100000, y32))) 4.7070644Погрешность: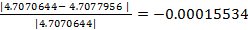
Date: 2015-07-17; view: 1032; Нарушение авторских прав