
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

ПРИЛОЖЕНИЯ. Приложение 1. Справочная информация о решении линейных дифференциальных уравнений 2 порядка
|
|
Приложение 1. Справочная информация о решении линейных дифференциальных уравнений 2 порядка.
Решением неоднородного дифференциального уравнения является суперпозиция общего решения  однородного уравнения и частного решения
однородного уравнения и частного решения  неоднородного уравнения.
неоднородного уравнения.
Если в правой части уравнения стоит многочлен k-й степени  , то частное решение неоднородного уравнения можно искать в виде многочлена той же степени
, то частное решение неоднородного уравнения можно искать в виде многочлена той же степени  .
.
Решение однородного уравнения 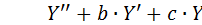
Характеристическое уравнение:
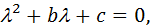
его решения – характеристические числа: 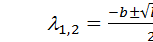
1. Если  , то
, то

Если 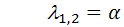 то общее решение можно записать в форме
то общее решение можно записать в форме
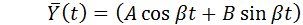
2. Если  , то
, то
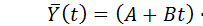
Приложение 2. Некоторые точки χ2-распределения
Таблица 1
Некоторые точки χ2-распределения

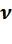
| 0,99 | 0,95 | 0,75 | 0,50 | 0,25 | 0,05 | 0,01 |
| 0.00016 | 0.00393 | 0.1015 | 0.4549 | 1.323 | 3.841 | 6.635 | |
| 0.02010 | 0.1026 | 0.5754 | 1.386 | 2.773 | 5.991 | 9.210 | |
| 0.1148 | 0.3518 | 1.213 | 2.366 | 4.108 | 7.815 | 11.34 | |
| 0.2971 | 0.7107 | 1.923 | 3.357 | 5.385 | 9.488 | 13.28 | |
| 0.5543 | 1.1455 | 2.675 | 4.351 | 6.626 | 11.07 | 15.09 | |
| 0.8721 | 1.635 | 3.455 | 5.348 | 7.841 | 12.59 | 16.81 | |
| 1.239 | 2.167 | 4.255 | 6.346 | 9.037 | 14.07 | 18.48 | |
| 1.646 | 2.733 | 5.071 | 7.344 | 10.22 | 15.51 | 20.09 | |
| 2.088 | 3.325 | 5.899 | 8.343 | 11.39 | 16.92 | 21.67 | |
| 2.558 | 3.940 | 6.737 | 9.342 | 12.55 | 18.31 | 23.21 | |
| 5.229 | 7.261 | 11.04 | 14.34 | 18.25 | 25.00 | 30.58 | |
| 8.260 | 10.85 | 15.45 | 19.34 | 23.83 | 31.41 | 37.57 | |
| 14.95 | 18.49 | 24.48 | 29.34 | 34.80 | 43.77 | 50.89 |
Пример.
Пусть для  получено экспериментально
получено экспериментально  . В строке таблицы 1, соответствующей
. В строке таблицы 1, соответствующей  , находим, что это значение соответствует
, находим, что это значение соответствует 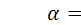 (меньше указанного для
(меньше указанного для 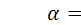 , но больше указанного для предыдущего
, но больше указанного для предыдущего  ). Следовательно, отклонение истинного распределения от идеального с вероятностью 0,75 обусловлено случайными причинами, а не тем, что наш генератор не способен генерировать равномерно распределенные случайные числа.
). Следовательно, отклонение истинного распределения от идеального с вероятностью 0,75 обусловлено случайными причинами, а не тем, что наш генератор не способен генерировать равномерно распределенные случайные числа.
Приложение 3. Основные сведения о законах распределения случайных величин
Функцией распределения F(x) случайной величины X называется вероятность того, что случайная величина X примет значение, меньшее x: 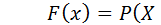 F(x) называют также интегральной функцией распределения или интегральным законом распределения (рис. 13).
F(x) называют также интегральной функцией распределения или интегральным законом распределения (рис. 13).
Плотностью распределения или дифференциальной функцией распределения (рис. 13) называют функцию 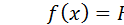
Важные соотношения:
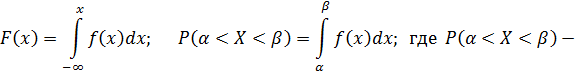
вероятность попадания величины X на отрезок 
Свойства функций распределения:
 – неубывающая функция; – неубывающая функция;
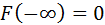
 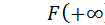
| 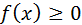
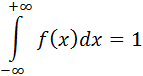
|
Математическое ожидание для непрерывного распределения выражается как
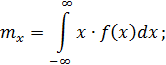
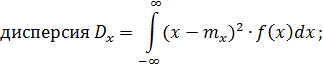
и, соответственно, среднее квадратическое отклонение  .
.
Нормальный закон распределения (закон Гаусса)
Наиболее часто на практике встречается нормальный закон распределения, часто называемый законом Гаусса. Он играет исключительно важную роль в теории вероятностей и занимает среди других законов распределения особое положение. Главная его особенность состоит в том, что он является предельным законом, к которому приближаются другие законы распределения при весьма часто встречающихся условиях. Большинство случайных величин (таких как ошибки измерений, стрельбы и т.д.) могут быть представлены как суммы большого числа сравнительно малых слагаемых – элементарных ошибок, каждая из которых вызвана действием одной какой-то причины. Каким бы законам распределения ни были подчинены отдельные элементарные ошибки, в сумме большого числа слагаемых их особенности нивелируются, и сумма оказывается подчиненной закону распределения, близкому к нормальному.
Одна из формулировок центральной предельной теоремы: «Для большого числа N случайных величин X с любым законом распределения их сумма есть случайное число с нормальным законом распределения при условии, что влияние на сумму отдельных слагаемых является равномерно малым[10]».
Формула распределения вероятности значений случайной величины x по нормальному закону имеет вид (рис. 16):

где x – случайная величина;
| Рис. 16. Нормальное распределение |
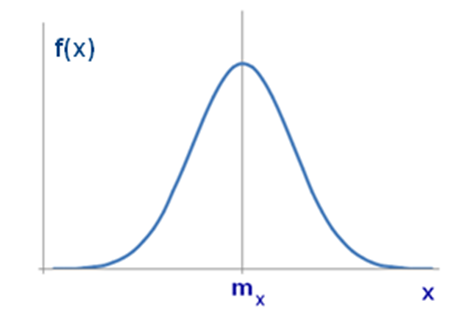 f (x) – вероятность принятия случайной величиной значения x;
f (x) – вероятность принятия случайной величиной значения x;
mx – математическое ожидание;
σx – среднее квадратичное отклонение.
Максимальная ордината кривой соответствует точке  и равна
и равна

По мере удаления от точки  кривая асимптотически приближается к оси абсцисс. Среднее квадратичное отклонение σx характеризует форму кривой: при уменьшении σx кривая вытягивается вверх, сужаясь с боков.
кривая асимптотически приближается к оси абсцисс. Среднее квадратичное отклонение σx характеризует форму кривой: при уменьшении σx кривая вытягивается вверх, сужаясь с боков.

| Рис. 17. Нормализованное нормальное распределение |

Распределение Пуассона
Говорят, что случайная дискретная величина X распределена по закону Пуассона, если вероятность того, что она примет определенное значение m, выражается формулой

Здесь a – параметр Пуассона или математическое ожидание случайной величины X. Кроме того, для распределения Пуассона
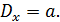
Приложение 4. Пример моделирования СМО
Условие задачи.
Составы с песком приходят на разгрузочный пункт с интенсивностью 6 шт. в сутки (простейший поток). В каждом составе от 5 до 14 вагонов, количество вагонов распределено равномерно. В каждом вагоне количество песка распределено нормально, m=20, σ=3. На пункте несколько погрузчиков, но с одним вагоном работает только один. Время, необходимое для разгрузки 1 тонны песка 6 мин. Время на подъезд погрузчика к вагону 3 мин. Время подачи состава с места ожидания на площадку 6 мин. Поезд не встает в очередь (уходит), если перед ним 3 состава. Определить простой погрузчиков и поездов, потерянную выручку из-за отчаявшихся машинистов и т.д.
Некоторый анализ системы.
Заявки – это, очевидно, подходящие составы. Поданные под разгрузку вагоны не образуют ординарный поток, но ординарным можно считать поток составов. Обслуживанием можно назвать процесс разгрузки состава. Можно считать, что заявке отказано в обслуживании, если в момент ее поступления в очереди 3 заявки. Время на подготовку к обслуживанию не требуется, следовательно, каналы горячие. Дисциплина обслуживания – First In, First Out.
Обсуждение алгоритма
Предлагается реализовать принцип последовательной проводки заявок, т.к. процесс ожидания заявки и процесс обслуживания не представляют интереса и являются довольно длительными, а канал обслуживания один. Считаем, что первый состав приходит на пункт в момент времени 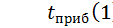 . К этому моменту все погрузчики свободны.
. К этому моменту все погрузчики свободны.
Определяем случайным образом время 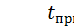 прибытия всех остальных поездов, считая поток поездов простейшим:
прибытия всех остальных поездов, считая поток поездов простейшим: 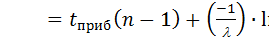 где
где  случайное равномерно распределенное число. Получим массив моментов появления заявок.
случайное равномерно распределенное число. Получим массив моментов появления заявок.
Следуя принципу последовательной проводки заявок, рассматриваем каждую заявку отдельно, сохраняя в специально созданном массиве время отправления разгруженного состава, т.к. оно определяет количество поездов в очереди на момент поступления очередной заявки и, следовательно, определяет, будет ли в обслуживании отказано.
Итак, для каждой i-й заявки определим сначала величину очереди: перебирая поезда с 1-го по i–1-й, подсчитаем количество составов, время отправления которых оказалось больше, чем время прибытия рассматриваемого i-го. Если в очереди больше трех составов, заявка отклоняется, а в качестве времени отправления ушедшему без обслуживания составу записывается ноль. Для обслуживаемой заявки определяем при помощи датчика случайных чисел количество вагонов и количество песка в каждом вагоне, назначаем исполнителя – один из погрузчиков. В массиве для каждого погрузчика указывается время его освобождения. Исполнителем становится либо свободный погрузчик (его время освобождения меньше времени начала разгрузки состава), либо тот, время освобождения которого минимально. Назначение погрузчику текущего вагона как задания есть переопределение времени освобождения.
Псевдокод алгоритма
ввод величин из условия задачи
n=1; 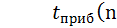 ;
; 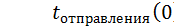 ;
; 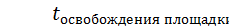
Пока не закончится время эксперимента
{ n=n+1; определяем  как время наступления события в простейшем потоке }
как время наступления события в простейшем потоке }
Для каждого погрузчика ( количество погрузчиков):
количество погрузчиков): 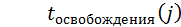
Для каждого i-го поезда (i=1..n)
{ определение длины очереди – подсчет количества еще не отправленных среди ранее пришедших составов;
если длина очереди >3, то
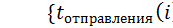 ; составу отказано в обслуживании }
; составу отказано в обслуживании }
иначе
{ если длина очереди =0, то
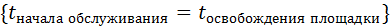
иначе
 };
};
количество вагонов в составе = равномерно распределенному от 5 до 14 случайному числу;
для каждого j-го вагона (j=1...количество вагонов)
{количество песка = нормально распределенному случайному числу;
определение свободного или освобождающегося первым погрузчика с номером k;
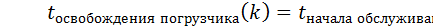 кол-во песка*скорость разгрузки + время для подхода к вагону}
кол-во песка*скорость разгрузки + время для подхода к вагону}
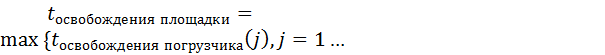 количество погрузчиков
количество погрузчиков 
} // конец обработки обслуженной заявки
} // конец обработки i-й заявки
время эксперимента = 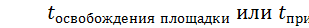
конец
Интересующие исследователя величины (такие как количество отклоненных заявок, среднее время простоя составов и погрузчиков) можно рассчитывать, вводя в алгоритм дополнительные переменные. Для сбора статистических данных лучше всего 1-й поезд не учитывать.
Список источников
1. Советов Б.Я., Яковлев С.А. Моделирование систем: Учебник для вузов – 3-е изд., перераб. и доп. –М.: Высшая школа, 2001. –343с.
2. Лоу А. М., Кельтон В. Д. Имитационное моделирование. Классика CS. – 3-е изд. – СПб.: Питер; Киев: Издательская группа BHV, 2004. –847 с.
3. Шеннон Р. Имитационное моделирование системю Искусство и наука/ Шеннон Р. –М.: Мир, 1978.
4. Вентцель Е.С. Задачи и упражнения по теории вероятностей: учебное пособие для студентов Втузов/ Е.С. Вентцель, Е.А. Овчаров –М.: Издательский центр "Академия", 2003.
5. Вентцель Е.С. Теория вероятностей (4-е издание). –М.: Наука, 1969. - 576 с.
6. Паничев В.В., Соловьев Н.А. Компьютерное моделирование. Учебное пособие/ –Оренбург, ГОУ ОГУ, 2008.
7. http://stratum.ac.ru/textbooks/modelir/contents.html
8. http://www.intuit.ru/department/mathematics/mathprog
Date: 2015-07-17; view: 602; Нарушение авторских прав