
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Иваново 2012 2 page
|
|
Очевидно, что требование простоты модели в каком-то смысле противоположно требованию ее адекватности. Впрочем, нередки случаи, когда усложнение модели может ухудшить ее адекватность (например, привлекаются параметры, известные с низкой точностью, или усложненные уравнения сомнительны.)
3. Полнота – это свойство, заключающееся в получении необходимого набора оценок характеристик системы.
4. Требование п родуктивности состоит в том, чтобы в реальных ситуациях исходные данные можно было бы считать заданными (их можно как-то получить: измерить, найти в справочниках), причём получение исходных данных должно быть легче, чем получение результирующих, иначе теряет смысл создание модели.
5. Требование робастности модели, т. е. ее устойчивости относительно погрешностей в исходных данных.
Этапы процесса моделирования
Процесс моделирования состоит из трёх основных стадий:
· формализация (переход от реального объекта к модели),
· моделирование (исследование и преобразования модели),
· интерпретация (перевод результатов моделирования в область реальности).
Более подробно процесс моделирования описывает жизненный цикл моделируемой системы:
· сбор информации об объекте, анализ системы, выдвижение гипотез, предмодельный анализ;
· проектирование структуры и состава моделей (подмоделей);
· построение спецификаций модели, разработка и отладка отдельных подмоделей, сборка модели в целом, идентификация (если это нужно) параметров моделей;
· исследование модели – выбор метода исследования и разработка алгоритма (программы) моделирования;
· исследование адекватности, устойчивости, чувствительности модели;
· оценка средств моделирования (затраченных ресурсов);
· интерпретация, анализ результатов моделирования и установление некоторых причинно-следственных связей в исследуемой системе;
· генерация отчетов и проектных (народно-хозяйственных) решений;
· уточнение, модификация модели, если это необходимо, и возврат к исследуемой системе с новыми знаниями, полученными с помощью моделирования.
СТАТИЧЕСКИЕ РЕГРЕССИОННЫЕ МОДЕЛИ
Понятие черного ящика и регрессии
В целях исследований иногда бывает удобно представить исследуемый объект в виде ящика, имеющего входы и выходы, не рассматривая детально его внутренней структуры.
Объект, о внутреннем строении которого ничего неизвестно, называют чёрным ящиком. Значения на входах и выходах черного ящика можно наблюдать и измерять.
Задача состоит в том, чтобы, зная множество значений на входах и выходах, построить модель, то есть определить функцию ящика, по которой вход преобразуется в выход. Такая задача называется задачей регрессионного анализа.
Регрессия в теории вероятностей и математической статистике – это зависимость среднего значения какой-либо величины от некоторой другой величины или от нескольких величин. В отличие от чисто функциональной зависимости у = f (х), когда каждому значению независимой переменной х соответствует одно определённое значение величины у, при регрессионной связи одному и тому же значению х могут соответствовать в зависимости от случая различные значения величины у.
Линейная одномерная регрессионная модель
| Y |
| X |
1. Гипотеза. Допустим, что зависимость между входом и выходом линейная (рис. 3): 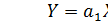 .
.
Тогда данная модель будет называться линейной одномерной регрессионной моделью.
2. Определение неизвестных коэффициентов a 0 и a 1 модели.
Для каждой из n снятых экспериментально точек ошибка Ei – это разность между экспериментальным значением Yi Эксп. и теоретическим значением Yi Теор., лежащим на гипотетической прямой 
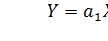 . Эти ошибки называют регрессионными остатками:
. Эти ошибки называют регрессионными остатками:
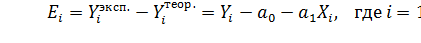 .
.
| Рис. 3. Результаты наблюдения над черным ящиком |
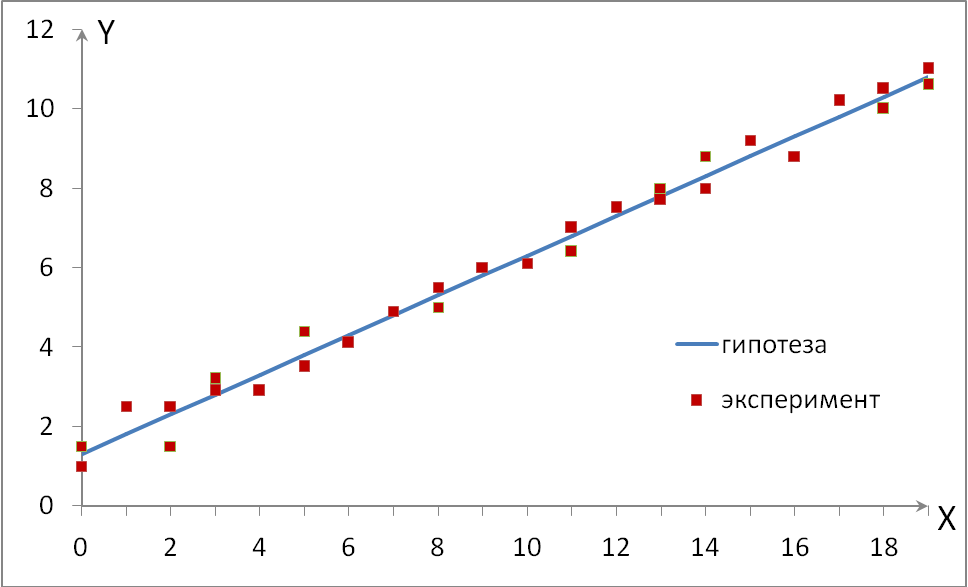
Все ошибки надо сложить. Чтобы положительные ошибки не компенсировали в сумме отрицательные, находят сумму квадратов регрессионных остатков F:
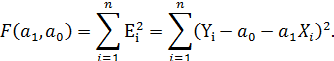
| (2) |
Меняя переменные a1 и a0, можно влиять на величину суммарной ошибки F, добиваясь того, чтобы она стала минимальной.
Условие минимума (частные производные функции F по переменным a1 и a0 равны нулю):
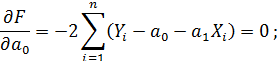
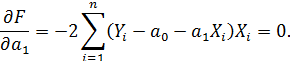
| (3) |
Получим систему уравнений
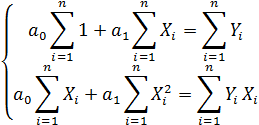
| (4) |
Решив систему (4), например, методом Крамера, получим:
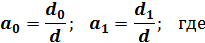
| (5) | |
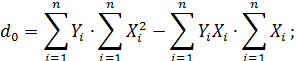
| ||
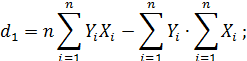
| 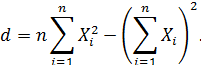
| |
Линейную регрессию часто называют методом наименьших квадратов, поскольку коэффициенты вычисляются из условия минимизации суммы квадратов ошибок (2).
3. Проверка гипотезы.
Для выяснения, насколько точен регрессионный анализ, используется сумма квадратов регрессионных остатков F(a0,a1) – мера рассеяния зависимой переменной вокруг линии регрессии.
Надо найти значение F, среднеквадратичное отклонение 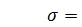 и расстояние
и расстояние 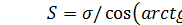 (см. рис. 4, 5).
(см. рис. 4, 5).
| α |
| α |
| X |
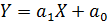
|
| Y Теор.+ S |
| S |
| σ |
| Y |
| Тангенс угла наклона прямой |
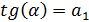
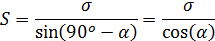
| Рис. 4. |
| X |
| YТеор.–S |
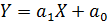
|
| Y Теор.+ S |
| S |
| 2σ |
| Y |
| Рис. 5. |
Если рассеяние (или среднеквадратичное отклонение) достаточно мало, и в полосу шириной 2σ (рис. 5), ограниченную линиями YТеор.–S и Y Теор.+ S, попадает 68.26% и более экспериментальных точек, то выдвинутая гипотеза принимается. В противном случае выбирают более сложную гипотезу или проверяют исходные данные.
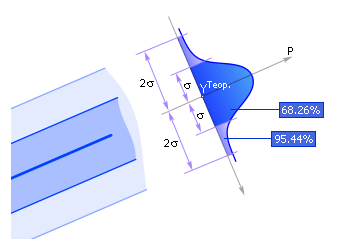
| Рис. 6. Нормальное распределение случайной величины |
Условия принятия гипотезы получены из нормального закона распределения случайных ошибок – закона Гаусса (рис. 6). Здесь P – вероятность распределения нормальной ошибки.
Линейная множественная регрессионная модель
| X2 |
| Y |
| X1 |
| Xm |
Тогда
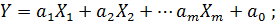
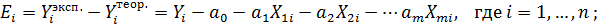
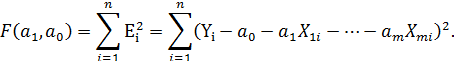
Для нахождения экстремума получим систему из m+1 уравнения:
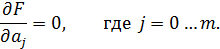
Такие системы имеет смысл решать методом Крамера, поэтому запишем её в матричном виде:
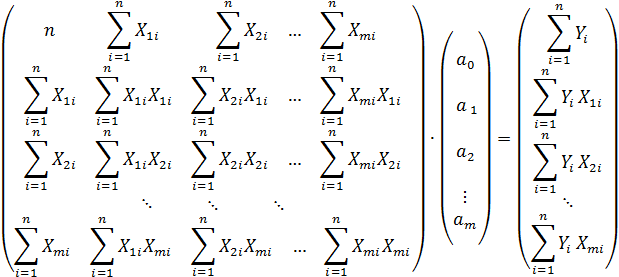
Вычисляем коэффициенты: 
Далее, по аналогии с одномерной моделью, для каждой точки вычисляется ошибка Ei; затем находится суммарная ошибка F и значения σ и S с целью определить, принимается ли выдвинутая гипотеза.
Нелинейные регрессионные модели
В некоторых случаях нелинейные зависимости можно представить в виде линейных путём введения дополнительных коэффициентов. Рассмотрим несколько вариантов.
| X2 |
| Y |
| X1 |
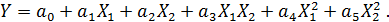
Если обозначить
| X2 |
| Y |
| X1 |
| Z1 |
| Z2 |
| Z3 |
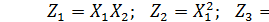
и считать 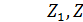 дополнительными входами, то получим линейную множественную регрессионную модель.
дополнительными входами, то получим линейную множественную регрессионную модель.
| X2 |
| Y |
| X1 |
| Xm |
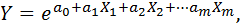
то прологарифмировав левую и правую части уравнения и обозначив  , получим
, получим
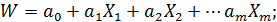
т.е. линейную множественную модель.
3. В случае обратной зависимости:
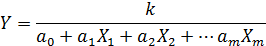
можно обозначить
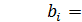

и снова перейти к линейной множественной модели
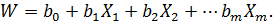
ДИНАМИЧЕСКИЕ МОДЕЛИ
Динамические системы
| Y(t) |
| X(t) |
В записи модели динамических систем присутствует производная, связывающая прошлое состояние системы с настоящим. Чем большей памятью обладает система, тем больше состояний из прошлого влияют на настоящее, тем большая степень старшей производной используется в записи модели, и тем больше параметров надо определить, чтобы идентифицировать систему[3]. Чтобы определить параметры системы необходимо, в первую очередь, оценить ее порядок.
Порядок динамической системы – это степень наибольшей из производных Y по отношению к t.
Динамическая система первого порядка
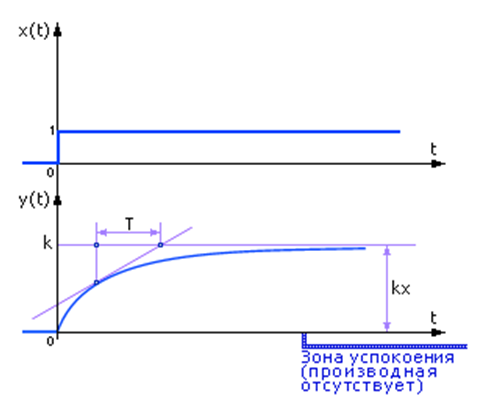
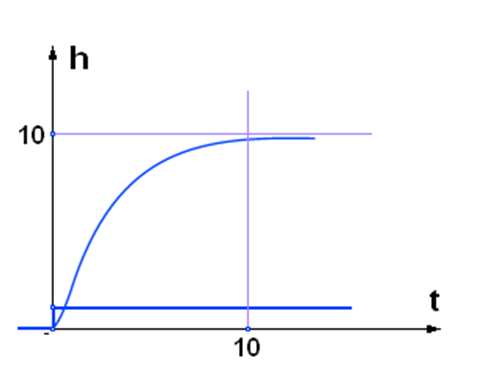
Рассмотрим входной и выходной сигналы, типичные для системы первого порядка (рис. 7).
| Рис. 7. Реакция системы 1-го порядка на единичный входной сигнал |
| а) |
| б) |
Пусть на вход системы, до того находившейся в покое, подали единичный сигнал 1[t] – единичная функция Хэвисайда (она изображена как зависимость x(t) на рис. 7а). Такой сигнал является одним из нескольких эталонных испытательных сигналов[4]. Если на вход подается сигнал в виде функции Хэвисайда при нулевых начальных условиях, то реакция на выходе будет называться переходной функцией или переходной характеристикой h(t) (рис. 7б).
Ожидается, что система на выходе должна увеличить сигнал x в k раз и дойти до значения kx. Параметр k называют коэффициентом усиления входного сигнала.
Сигнал на выходе нарастает постепенно, инерционно. Переход от нуля до kx – процесс динамический, в сигнале присутствует изменение, которое описывается производной, и выход оказывается меньше входа на некоторую величину f: 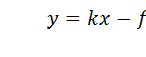 .
.
Если на выходе наблюдается экспоненциальный сигнал, то f выражается как 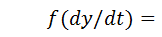 , где параметр T – инерционность системы, является константой. Тогда система называется системой (или звеном) первого порядка, а ее поведение описывается уравнением
, где параметр T – инерционность системы, является константой. Тогда система называется системой (или звеном) первого порядка, а ее поведение описывается уравнением 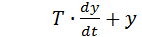 с двумя параметрами T и k.
с двумя параметрами T и k.
Чтобы определить, является ли кривая экспонентой, в каждой ее точке проводится касательная до пересечения с линией установившегося уровня (на рис. 7 это линия y(t)=k). Если кривая является экспонентой, то величина T в любой точке будет постоянной.
При определении модели требуется найти неизвестные коэффициенты k и T. Коэффициент k характеризует способность системы к усилению, а T – инерционность системы (память). Чем больше T, тем медленнее система реагирует на входной сигнал.
Звено второго порядка (колебательное звено)
Такие звенья описываются дифференциальным уравнением вида: 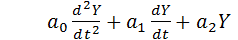 , где U – входные воздействия.
, где U – входные воздействия.
Если ввести обозначения 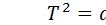 ;
; 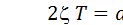 ;
; 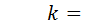 ; то уравнение примет вид
; то уравнение примет вид
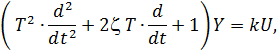
в записи которого содержатся три параметра:
T – постоянная времени (в секундах);
 – коэффициент затухания (безразмерная величина);
– коэффициент затухания (безразмерная величина);
k – передаточный коэффициент.
Если входное воздействие U=0, то можно получить так называемое характеристическое уравнение
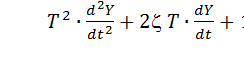 ,
,
касающееся только внутренних свойств звена.
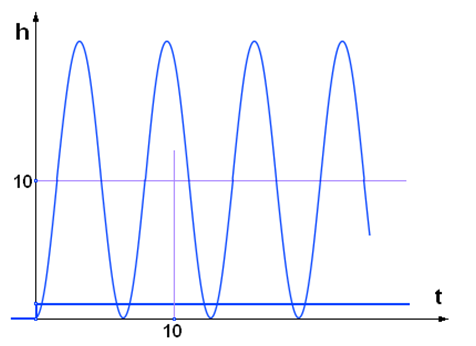
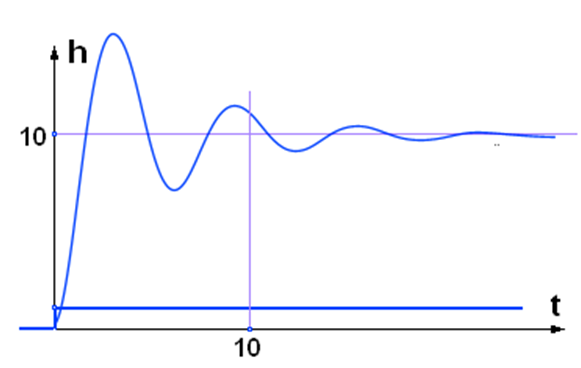
В зависимости от величины  звенья второго порядка классифицируются по видам:
звенья второго порядка классифицируются по видам:
 = 0 – консервативное звено второго порядка (рис. 8а);
= 0 – консервативное звено второго порядка (рис. 8а);
0 <  < 1 – колебательное звено второго порядка (рис. 8б);
< 1 – колебательное звено второго порядка (рис. 8б);
 ≥ 1 – апериодическое звено второго порядка (рис. 8в).
≥ 1 – апериодическое звено второго порядка (рис. 8в).
| а) |
| б) |
| в) |
Рис. 8. Переходные характеристики h(t) звеньев 2-го порядка в зависимости от параметра  : а)
: а)  = 0;
= 0;
б)  = 0,2;
= 0,2;
в)  = 1,5.
= 1,5.
Динамические регрессионные модели
Допустим, что на вход системы подана сигнал в виде функции Хэвисайда, а примерный вид динамического сигнала представлен на рис. 9а. Ограничиваясь временем рассмотрения сигнала, равным T, проведена дискретизация сигнала (рис. 9б) – разбиение отрезка [0;T] на n равных промежутков.
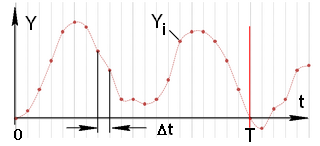
| а) |
| б) |
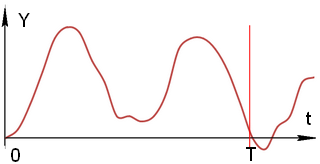
Рис. 9. Возможный вид зависимости выходного сигнала от времени а) до дискретизации; б) после дискретизации
Пусть на вход системы подается единичная функция Хэвисайда 1[t], а выходной сигнал описывается уравнением[5]
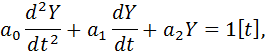
| (6) |
с начальными условиями 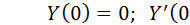
| (7) |
Проинтегрируем уравнение (6) дважды от 0 до некоторого произвольного t, учитывая условия (7). После первого интегрирования получим:
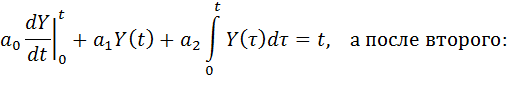
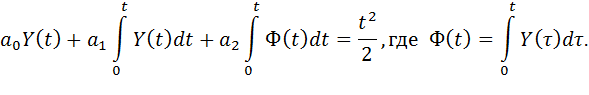
Переходя к численному интегрированию методом правых прямоугольников, получим для любого m = 1,2,...,n:
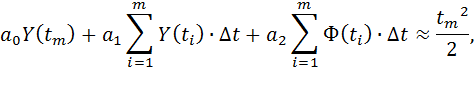
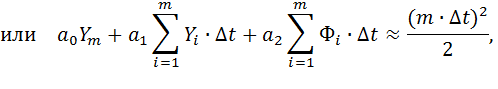
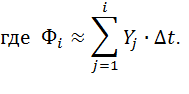
Следовательно, для каждого m = 1,2,...,n (n – число экспериментальных точек) приблизительно верно:
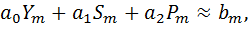
| (8) |
если использовать обозначения
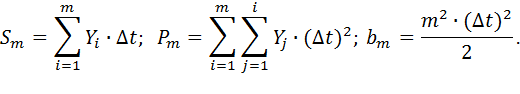
| (9) |
Ошибку  , которая показывает, насколько отходит теоретическое значение
, которая показывает, насколько отходит теоретическое значение  от экспериментального в некоторой m -ой точке, можно записать как
от экспериментального в некоторой m -ой точке, можно записать как
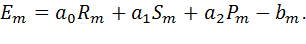
Сумма квадратов ошибок, вносимых всеми точками, которую надо минимизировать, будет:
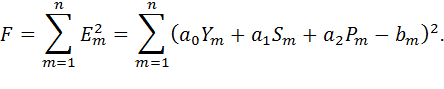
| (10) |
Чтобы найти минимум функции F, доставляемый за счет параметров a0, a1, a2, надо взять частные производные F по каждому из параметров и приравнять каждую производную к нулю. В результате получаем систему линейных уравнений:
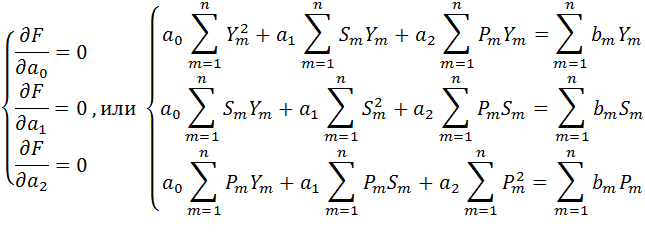

Запишем систему в матричном виде, и решим ее методом Крамера. Можно считать, что задача нахождения коэффициентов модели решена, а система описывается уравнением (6) с начальными условиями (7) и определенными постоянными коэффициентами 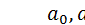
Теперь необходимо сравнить получаемое из этой модели решение Y теоретическое с Y, заданным экспериментально, и вычислить ошибку F. Далее проверить ее значение по критерию – допустимо ли значение вычисленной ошибки, или гипотезу о виде модели требуется сменить на более точную.
Y теоретическое можно получить, аналитически решая дифференциальное уравнение (6)[6].
Считая что коэффициенты модели теперь известны, построим реализацию, имитирующую поведение системы.
Для этого воспользуемся уже полученной ранее формулой (8) с учетом введенных обозначений (9). Поскольку
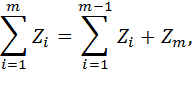
из выражения

можно выразить сначала  , а потом
, а потом 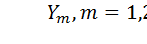 тем самым сымитировав поведение системы.
тем самым сымитировав поведение системы.
Модель в виде фильтра Каллмана
Каллманом была доказана теорема о том, что любой динамический сигнал может быть представлен в виде:
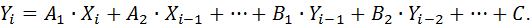
| (11) |
Идея фильтра Каллмана заключается в том, что выход системы в i -й момент времени определяется входным сигналом, его предысторией и предысторией самого состояния системы.
Чем больше имеется членов ряда, то есть чем больше переменных Y учитывается в записи модели, тем глубже память системы. Заметим, что наличие члена  в модели динамической системы (11) соответствует наличию первой производной,
в модели динамической системы (11) соответствует наличию первой производной,  – второй производной и т. д.
– второй производной и т. д.
Ошибка между значением экспериментально снятой точки и теоретическим ее значением (гипотезой) выразится как:
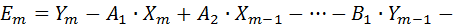
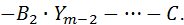
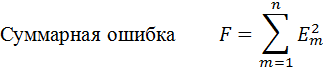
должна быть минимизирована относительно определяемых переменных A 1, A 2, …, B 1, B 2, …, C:
Если взять частные производные от F по параметрам A 1, A 2, …, B 1, B 2, …, C и приравнять их к нулю, получим линейную множественную регрессионную модель, из которой определяются неизвестные коэффициенты уравнения (11).
СТАТИСТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
Понятие статистического моделирования
Статистическое моделирование используется при исследовании сложных систем, подверженных случайным возмущениям. Возможно построение вероятностных аналитических моделей и вероятностных имитационных моделей.
В вероятностных аналитических моделях влияние случайных факторов учитывается с помощью задания вероятностных характеристик случайных процессов (законов распределения вероятностей, например). Поскольку построение таких моделей представляет собой сложную вычислительную задачу, вероятностное аналитическое моделирование используют для изучения сравнительно простых систем.
Подмечено, что введение случайных возмущений в имитационные модели не вносит принципиальных усложнений, поэтому исследование сложных случайных процессов проводится, как правило, на имитационных моделях.
В вероятностном имитационном моделировании оперируют не характеристиками случайных процессов, а конкретными случайными числами – значениями параметров. Следовательно, результаты, полученные на имитационной модели, являются случайными реализациями. Поэтому для нахождения объективных и устойчивых характеристик процесса требуется многократное воспроизведение компьютерного эксперимента с последующей статистической обработкой полученных данных. Именно по этой причине исследование с помощью вероятностного имитационного моделирования принято называть статистическим моделированием.
Итак, статистическое моделирование – это способ изучения сложных процессов и систем, подверженных случайным возмущениям, с помощью имитационных моделей.
В основе статистического моделирования лежит метод Монте-Карло.
Метод Монте-Карло.
Сначала Энрико Ферми в 1930-х годах в Италии, а затем Джон фон Нейман и Станислав Улам в 1940-х в Лос-Аламосе предложили использовать стохастический подход для аппроксимации многомерных интегралов.
Идея была развита Уламом, который вынужденно бездельничал во время болезни, и, раскладывая пасьянсы, задался вопросом, какова вероятность того, что пасьянс «сложится». Ему в голову пришла идея, что вместо того, чтобы использовать соображения комбинаторики, можно просто поставить «эксперимент» большое число раз и, подсчитав число удачных исходов, оценить их вероятность.
Годом рождения метода считается 1949 год, когда в свет вышла статья Метрополиса и Улама «Метод Монте-Карло»[7].
Появление электронных компьютеров, которые могли с большой скоростью генерировать псевдослучайные числа, резко расширило круг задач, для решения которых стохастический подход оказался более эффективным, чем другие математические методы.
Использование метода заключается в многократном повторении компьютерного эксперимента и статистическом анализе полученной серии результатов.
| Рис. 10. Определение значения интеграла методом Монте-Карло |
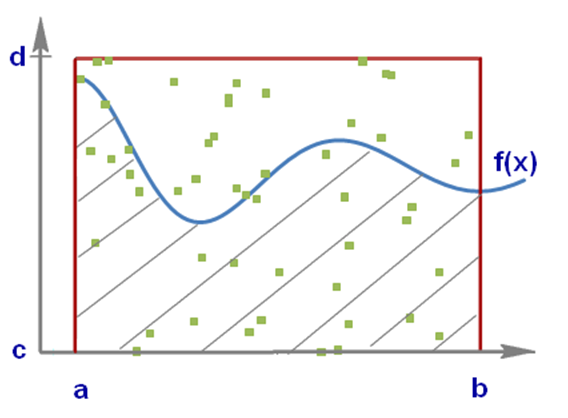 Рассмотрим вычисление интеграла методом Монте-Карло (рис. 10). Пусть задана некоторая функция
Рассмотрим вычисление интеграла методом Монте-Карло (рис. 10). Пусть задана некоторая функция  . Задача состоит в том, чтобы определить
. Задача состоит в том, чтобы определить 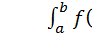 , т.е. найти площадь под графиком
, т.е. найти площадь под графиком  на рис. 10.
на рис. 10.
Ограничиваем кривую прямоугольником поиска и распределяем в нем точки случайным образом. Если  – количество точек под кривой, а
– количество точек под кривой, а  – общее количество точек, то
– общее количество точек, то
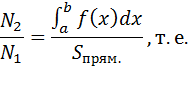
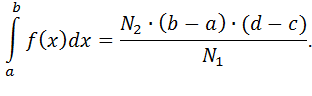
Метод Монте-Карло эффективен и прост, но необходим «хороший» генератор случайных чисел. Вторая проблема заключается в определении количества точек, необходимых для обеспечения решения с заданной точностью (объема выборки). Эксперименты показывают, что точность примерно пропорциональна корню квадратному из объема выборки: чтобы увеличить точность в 10 раз, объем выборки нужно увеличить в 100 раз.
Date: 2015-07-17; view: 485; Нарушение авторских прав